Простейшие преобразования декартовой системы координат. Параллельныйсдвиг осей координат.

П

УСТЬ ТОЧКА В СИСТЕМЕ КООРДИНАТ ИМЕЕТ КООРДИНАТЫ . ПОМЕСТИМ НАЧАЛО НОВОЙ СИСТЕМЫ КООРДИНАТ В ТОЧКУ . ОСЬ НАПРАВИМ ПАРАЛЛЕЛЬНО ОСИ , А ОСЬ ПАРАЛЛЕЛЬНО ОСИ . ТОГДА В НОВОЙ СИСТЕМЕ КООРДИНАТ ТОЧКА БУДЕТ ИМЕТЬ КООРДИНАТЫ (РИС.13) . ЕСЛИ ТЕПЕРЬ НА ПЛОСКОСТИ РАССМОТРИМ ПРОИЗВОЛЬНУЮ ТОЧКУ , ИМЕЮЩУЮ В СТАРОЙ СИСТЕМЕ КООРДИНАТ КООРДИНАТЫ , ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ ТОЧКА БУДЕТ ИМЕТЬ КООРДИНАТЫ

ПЕРЕХОД ОТ КООРДИНАТНОЙ СИСТЕМЫ К СИСТЕМЕ НАЗОВЕМ ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ КООРДИНАТ (РИС.13).

РИС.13

П

РИМЕР 2.5. НА РИС.14 ПРИВЕДЁН ЧЕРТЁЖ ПАРАБОЛЫ И ВЫПИСАНЫ ЕЁ УРАВНЕНИЯ В СТАРОЙ И НОВОЙ СИСТЕМАХ ДЕКАРТОВЫХ КООРДИНАТ. НОВАЯ СИСТЕМА ПОЛУЧЕНА ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ СТАРОЙ СИСТЕМЫ.

2

1

РИС.14

В СТАРОЙ СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД

В НОВОЙ «КАНОНИЧЕСКОЙ» СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД

(СМ. ФОРМУЛУ (2.19))

. ЛИНИЯ ПАРАБОЛА.

ЗАМЕЧАНИЕ. ПРИВЕДЁМ ПРИМЕР ЧЕРТЕЖА ПАРАБОЛЫ, У КОТОРОЙ УРАВНЕНИЕ НЕ КАНОНИЧЕСКОЕ. В ДАННОМ СЛУЧАЕ ДЛЯ ПОЛУЧЕНИЯ «КАНОНИЧЕСКОЙ» СИСТЕМЫ КООРДИНАТ ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ .

В

ДЕКАРТОВОЙ ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ , КОТОРАЯ НЕ ЯВЛЯЕТСЯ «КАНОНИЧЕСКОЙ» , УРАВНЕНИЕ ПАРАБОЛЫ В ОБЩЕМ СЛУЧАЕ ИМЕЕТ ВИД: . КРИВАЯ ПАРАБОЛЫ НЕ СИММЕТРИЧНА НИ ОДНОЙ ИЗ КООРДИНАТНЫХ ОСЕЙ. ЕСЛИ ПАРАЛЛЕЛЬНЫМ СДВИГОМ СИСТЕМЫ КООРДИНАТ НАЧАЛО КООРДИНАТ ПЕРЕМЕСТИТЬ В ВЕРШИНУ ПАРАБОЛЫ В ТОЧКУ , А ЗАТЕМ ОСИ ПОВЕРНУТЬ СОГЛАСНО РИСУНКУ, ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ПАРАБОЛЫ СТАНОВИТСЯ КАНОНИЧЕСКИМ (РИС15)

РИС.15

П

РИМЕР 2.6 НА РИС.16 ПРИВЕДЁН ЧЕРТЁЖ ЭЛЛИПСА И ВЫПИСАНЫ ЕГО УРАВНЕНИЯ В СТАРОЙ И НОВОЙ СИСТЕМАХ ДЕКАРТОВЫХ КООРДИНАТ. НОВАЯ СИСТЕМА ПОЛУЧЕНА ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ СТАРОЙ СИСТЕМЫ.

3

1

РИС.16

В СТАРОЙ СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД

В НОВОЙ «КАНОНИЧЕСКОЙ» СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД

(СМ. ФОРМУЛУ (2.19)) . ЛИНИЯ ЭЛЛИПС.

З

АМЕЧАНИЕ. ПРИВЕДЁМ ПРИМЕР ЧЕРТЕЖА ЭЛЛИПСА, У КОТОРОГО УРАВНЕНИЕ НЕ КАНОНИЧЕСКОЕ. В ДАННОМ СЛУЧАЕ ДЛЯ ПОЛУЧЕНИЯ «КАНОНИЧЕСКОЙ» СИСТЕМЫ КООРДИНАТ ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ .

В

ДЕКАРТОВОЙ ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ , КОТОРАЯ НЕ ЯВЛЯЕТСЯ «КАНОНИЧЕСКОЙ» , УРАВНЕНИЕ ЭЛЛИПСА ОБЫЧНО ИМЕЕТ ВИД: КРИВАЯ ЭЛЛИПСА НЕ СИММЕТРИЧНА ОТНОСИТЕЛЬНО КООРДИНАТНЫХ ОСЕЙ. ЕСЛИ НАЧАЛО КООРДИНАТ ПЕРЕМЕСТИТЬ В ЦЕНТР СИММЕТРИИ ЭЛЛИПСА ТОЧКУ , А ОСИ ПОВЕРНУТЬ СОГЛАСНО РИСУНКУ, ТО В НОВОЙ СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ЭЛЛИПСА СТАНОВИТСЯ КАНОНИЧЕСКИМ (РИС.17)

РИС.17

ПРИМЕР 2.7. НА РИС.18 ПРИВЕДЁН ЧЕРТЁЖ ГИПЕРБОЛЫ И ВЫПИСАНЫ ЕЁ УРАВНЕНИЯ В СТАРОЙ И НОВОЙ СИСТЕМАХ ДЕКАРТОВЫХ КООРДИНАТ. НОВАЯ СИСТЕМА ПОЛУЧЕНА ПАРАЛЛЕЛЬНЫМ СДВИГОМ ОСЕЙ СТАРОЙ СИСТЕМЫ.

1

3

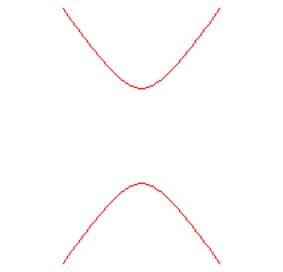
РИС.17

В СТАРОЙ СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ЛИНИИ ИМЕЕТ ВИД

В НОВОЙ «КАНОНИЧЕСКОЙ» СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ЛИНИИ ИМЕЕТ КАНОНИЧЕСКИЙ ВИД

(СМ. ФОРМУЛУ (2.19))

. ЛИНИЯ ГИПЕРБОЛА.

ЗАМЕЧАНИЕ. ПРИВЕДЁМ ПРИМЕР ЧЕРТЕЖА ГИПЕРБОЛЫ, У КОТОРОЙ УРАВНЕНИЕ НЕ КАНОНИЧЕСКОЕ. В ДАННОМ СЛУЧАЕ ДЛЯ ПОЛУЧЕНИЯ КАНОНИЧЕСКОЙ СИСТЕМЫ КООРДИНАТ ТРЕБУЕТСЯ СОВЕРШИТЬ ПАРАЛЛЕЛЬНЫЙ СДВИГ ОСЕЙ И ЗАТЕМ ПОВОРОТ СТАРОЙ СИСТЕМЫ КООРДИНАТ .

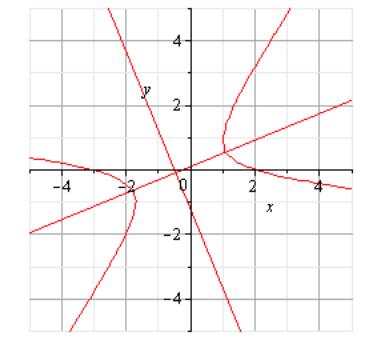
В ДЕКАРТОВОЙ ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ , КОТОРАЯ НЕ ЯВЛЯЕТСЯ «КАНОНИЧЕСКОЙ», КРИВАЯ ВЫГЛЯДИТ ТАК. ЕСЛИ НАЧАЛО КООРДИНАТ ПЕРЕМЕСТИТЬ ПАРАЛЛЕЛЬНЫМ СДВИГОМ В ЦЕНТР СИММЕТРИИ ГИПЕРБОЛЫ В ТОЧКУ , А ЗАТЕМ ОСИ ПОВЕРНУТЬ СОГЛАСНО РИСУНКУ, ТО В НОВОЙ «КАНОНИЧЕСКОЙ» СИСТЕМЕ КООРДИНАТ УРАВНЕНИЕ ГИПЕРБОЛЫ СТАНОВИТСЯ КАНОНИЧЕСКИМ (РИС.18)

РИС.18