
ЕГЭ / Математика / МАТЕМАТИКА ЕГЭ 2011 (типовые задания С2)
.pdfКорянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
МАТЕМАТИКА ЕГЭ 2011 (типовые задания С2)
Многогранники:
виды задач и методы их решения
Корянов А. Г., г. Брянск, akoryanov@mail.ru Прокофьев А.А., г. Москва, aaprokof@yandex.ru
СОДЕРЖАНИЕ стр.
1. Расстояния и углы |
2 |
1.1. Расстояние между двумя точками |
2 |
1.2.Расстояние от точки до прямой…. 3
1.3.Расстояние от точки до плоскости 6
1.4.Расстояние между скрещивающимися прямыми…………………….. 11
1.5.Угол между двумя прямыми......... 16
1.6.Угол между прямой и плоско-
стью…………………………………… 21
1.7. Угол между плоскостями |
25 |
2. Площади и объемы……………….. 40
2.1.Площадь поверхности много-
гранника ………………………………. 40
2.2.Площадь сечения многогранника 43
2.3.Объем многогранника…………… 47
3. Задачи на экстремум…..………. 59
3.1.Аналитический метод…………… 59
3.2.Геометрический метод.….…........ 60
4. Дополнения……………………… 62
4.1.Построение сечения многогран-
ника……………………………………. 62
4.2.Векторный метод………………… 67
4.3.Координатный метод…………….. 71
4.4.Опорные задачи………………….. 74
Упражнения………………………….. 81
Ответы………………………………... 88
Список и источники литературы…. 89
Введение
Задачи части «С» Единого государственного экзамена по стереометрии в последнее время большей частью посвящены вычислению расстояний и углов в пространстве. Такие задачи часто встречаются в практике, поэтому им уделено особое внимание.
Ниже представлены разные методы решения этих задач. Традиционный метод решения задачи опирается на определения расстояния или угла, и требует от учащихся развитого пространственного воображения. Кроме этого подхода в пособии рассмотрены координатный и векторный методы, которые могут быть эффективно использованы при решении задач разного вида. Применение опорных задач может привести к рациональному решению задачи.
Вкодификатор элементов содержания
куровню подготовки выпускников входят разделы, связанные с темой «Многогранники», которые отражены в данном пособии: сечения куба, призмы, пирамиды; боковая поверхность призмы, пирамиды; объем куба, прямоугольного параллелепипеда, пирамиды, призмы; примеры использования производной для нахождения наилучшего решения в прикладных задачах.
Врешениях многих задач, приведенных в данном пособии, имеются ссылки на опорные задачи, полный набор которых помещен в пункте 4.4 на стр. 75-80.
18.02.2011 |
1 |
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
1. Расстояния и углы
Тема «Расстояния и углы» является основой для других разделов стереометрии. В данном разделе представлено взаимное расположение точек, прямых и плоскостей на многогранниках, рассмотрены основные виды задач и методы их решения.
1.1. Расстояние между двумя точками
Расстояние между точками A и B можно вычислить:
1) как длину отрезка AB , если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон;
2) по формуле
A, B 
 (x2 x1)2 (y2 y1)2 (z2 z1)2 ,
(x2 x1)2 (y2 y1)2 (z2 z1)2 ,
где A(x1, y1, z1), B(x2, y2, z2);
|
|
|
|
|
|
|
|
3) по формуле |
AB |
|
AB AB , или |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
AB |
|
a2 b2 c2 , где {a, b, c} – коор- |
|||||
|
|
|
|
|
|
|
|
динаты вектора AB .
поэтапно-вычислительный метод
Пример 1. В единичном кубе
ABCDA1B1C1D1 |
на диагоналях граней |
||||||||
AD1 |
и D1B1 |
взяты точки Е и F так, что |
|||||||
D E |
1 |
AD , D F |
2 |
D B . Найти длину |
|||||
|
|
||||||||
1 |
3 |
1 |
1 |
3 |
|
1 |
1 |
||
отрезка EF. |
|
|
|
|
|
|
|||
|
|
|
|
|
B1 |
|
|
||
|
|
|
A1 |
|
|
F |
|
C1 |
|
|
|
|
|
|
|
|
|
|
|

 E
E D1
D1


 B
B 


A




 C
C
D
Рис. 1
Решение. Длину отрезка EF найдем по теореме косинусов из треугольника D1EF (см. рис. 1), в котором
D F |
2 |
|
|
, |
D E |
1 |
|
|
, |
FD E |
|
|
|
2 |
2 |
||||||||||
|
|
|
|
|||||||||
1 |
3 |
|
|
|
1 |
3 |
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
18.02.2011 |
|
|
|
|
|
|
|
|
2 |
|||
(треугольник AB1D1 является равносторонним). Имеем
EF2 D E2 |
|
D F2 2D E D F cos |
|
|
|
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
1 |
|
|
1 |
|
|
1 |
|
1 |
3 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
8 |
2 |
|
2 |
|
|
2 |
2 |
|
|
1 |
|
2 |
, |
|
|
|
|
|
||||||
|
9 |
3 |
|
|
|
|
|
3 |
|
|
|
||||||||||||||||
9 |
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
||||||||||||
откуда EF |
|
|
|
6 |
|
. |
|
|
|
|
|
|
|
Ответ: |
|
6 |
|
. |
|||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||||
|
координатный метод |
|
|
|
|
|
|
|
|
||||||||||||||||||
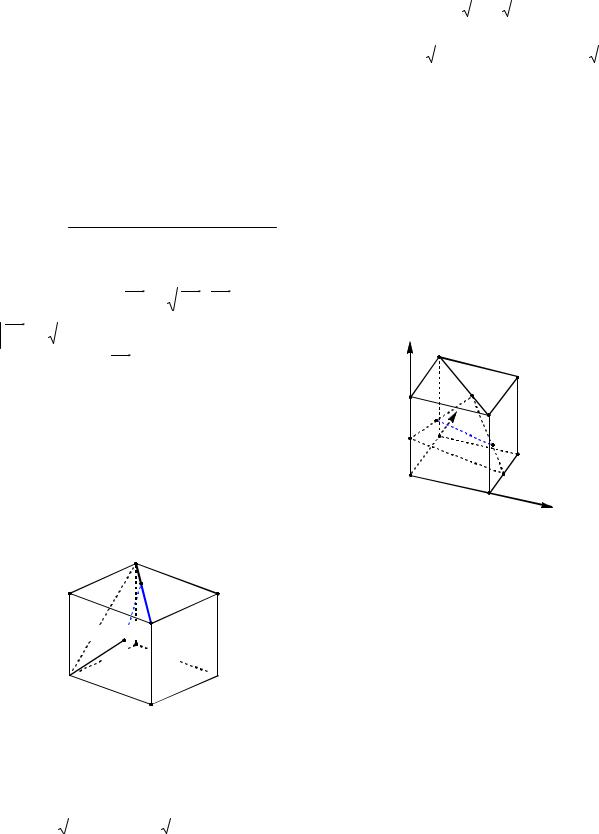
Пример 2. В единичном кубе ABCDA1B1C1D1 точки E и K – середины ребер AA1 и CD соответственно, а точка M расположена на диагонали B1D1 так, что B1M 2MD1. Найти расстояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МК такая, что ML 2LK.
Решение. Введем прямоугольную систему координат, как указано на рисунке 2.
z |
B1 |
|
|
|
|
|
|
||
A1 |
|
|
|
|
M |
|
|
C1 |
|
|
|
|
|
|
|
|
|
||
|
Q |
|
y |
D1 |
|
|
|||
E |
B |
|
|
L |
C |
|
|||
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
K |
|
|
|
|
|
|
D |
|
|
|||
|
|
|
|
|
|
x |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
||
Тогда Е 0;0; |
|
|
|
, K 1; |
|
;0 |
, В (0;1;1), |
||
|
2 |
|
|
|
2 |
|
1 |
||
D1(1;0;1). |
Для |
|
нахождения |
координат |
|||||
точки М используем формулу координат точки (опорная задача 1), делящей отре-
зок B1D1 в отношении 2:1. Имеем |
|
|||||||||||
0 2 1 1 2 0 1 2 1 |
|
2 1 |
|
|
||||||||
М |
|
, |
|
, |
|
|
|
|
, |
|
|
,1 . |
|
|
|
|
|
||||||||
|
1 2 |
1 2 |
1 2 |
3 3 |
|
|||||||
Аналогично получим координаты точки L, делящей отрезок MK в отношении 2:1. Имеем
|
2 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 1 |
|
|
|
2 |
|
|
|
1 2 0 |
|
|
8 4 1 |
|
||||||
|
|
3 |
|
|||||||||||||||||
L |
3 |
|
; |
2 |
; |
|
|
|
|
; |
|
; |
|
. |
||||||
|
|
|
|
|
|
|
||||||||||||||
1 2 |
|
|
|
1 2 |
1 2 |
9 9 3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Координаты точки Q равны полусуммам соответствующих координат точек E и
|
1 |
|
1 |
|
3 |
|
|
М, поэтому Q |
|
; |
|
; |
|
|
. Применим фор- |
|
6 |
4 |
|||||
3 |
|
|
|
||||
мулу для расстояния между точками с заданными координатами
LQ |
|
|
1 |
|
|
8 |
2 |
1 |
|
4 |
2 |
|
3 |
|
1 |
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
3 |
|
|
9 |
6 |
|
9 |
4 |
|
3 |
|
|
|
|
|||||||||||
|
|
|
|
|
5 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
725 |
|
|
29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
362 |
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
29 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
векторный метод
Пример 3. В единичном кубе ABCDA1B1C1D1 на диагоналях граней
AD1 и D1B1 взяты точки E и F так, что
D E |
1 |
AD , |
D F |
2 |
|
D B . Найти длину |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
3 |
|
1 |
|
|
1 |
|
|
|
|
|
3 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
отрезка EF. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Решение. |
|
|
|
Пусть |
|
|
|
|
AD a , |
|
|
|
|
|
|
|
AB b , |
|||||||||||||||||||||||||||||||||||||||||||||||
AA1 c (см. |
рис. |
|
|
|
1), |
|
|
тогда |
|
|
| a | |b | |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c | 1, |
|
a b a |
c b c 0. |
|
|
|
|
Выразим |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вектор |
|
|
FE |
через базисные векторы a, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b, c : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
FE EA AB B F |
2 |
|
|
(a c) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
(b |
c) |
|
|
(a b) |
|
|
|
|
a |
|
|
|
|
|
|
b |
|
|
|
|
|
c . |
|||||||||||||||||||||||||||||||||||||||||||
3 |
3 |
|
|
3 |
3 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
FE |
|
|
FE |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
c |
|
|
||||||||||||||||||||||||||||||||||||
|
3 |
3 |
3 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
4 |
|
1 |
|
|
|
|
|
6 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
9 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
6 |
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Замечание. Вектор |
|
|
FE в данном ба- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
1 |
|
|
|
|
||||||||||||||||||||||
зисе имеет координаты |
|
|
|
|
|
; |
|
|
|
|
|
; |
|
|
|
|
, |
по- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
этому длину этого вектора можно найти |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
по формуле |
AB |
|
|
|
|
|
a2 b2 c2 , то есть |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
AB |
|
|
|
|
1 |
|
4 |
|
1 |
|
|
|
6 |
|
6 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
9 |
|
|
|
|
9 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
18.02.2011 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1.2.Расстояние от точки до прямой
Расстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.
Расстояние между двумя параллель-
ными прямыми равно длине отрезка их общего перпендикуляра.
Расстояние между двумя параллель-
ными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.
поэтапно-вычислительный метод
Расстояние от точки до прямой можно вычислить, как длину отрезка перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот.
Пример 4. При условиях примера 1 найти расстояние от точки D1 до прямой EF.
Решение. Пусть h – длина высоты треугольника D1EF, опущенной из точки
D1. Найдем h, используя метод площа-
дей. Площадь треугольника D1EF равна
1
2 D1F D1E sin FD1E
|
1 |
|
2 2 |
|
2 |
|
3 |
|
3 |
. |
|
|
3 |
2 |
|
||||||
2 |
3 |
|
|
9 |
|
|||||
С другой стороны площадь треугольника
D EF |
|
равна |
1 |
|
FE h |
6 |
h. Из уравне- |
|||||||||||
|
|
|
|
|
||||||||||||||
1 |
|
|
|
|
|
|
2 |
|
|
6 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
ния |
|
|
3 |
|
|
|
|
|
6 |
|
h находим искомое рас- |
|||||||
|
9 |
|
|
6 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
. |
|
|
|||||||||||
стояние h |
2 |
|
|
|||||||||||||||
3 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Замечание. Можно заметить, что выполняется равенство FE2 D1E2 D1F2 ,
т.е. треугольник D1EF прямоугольный и длина отрезка D1E является искомым расстоянием.
Ответ: 2 . 3
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
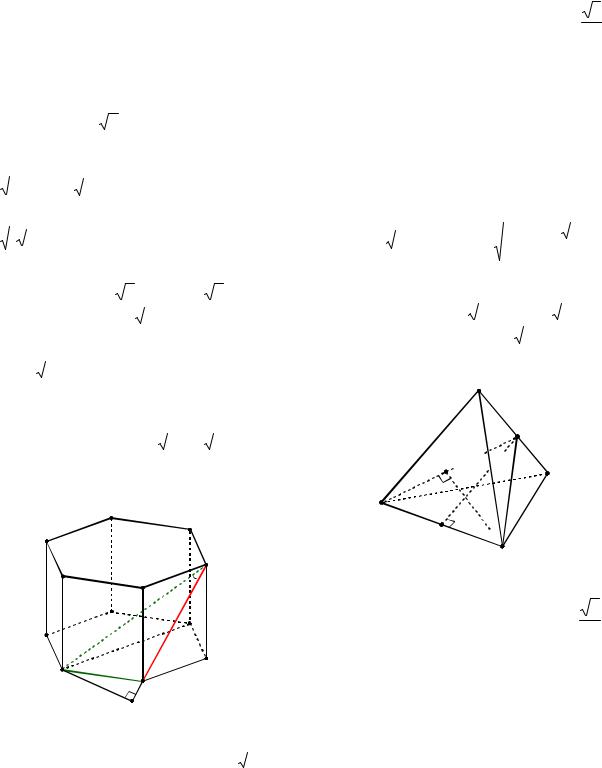
Пример 5. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны l, найти расстояние от точки A до прямой BC1.
Решение. В квадрате BCC1B1 диаго-
наль BC1 |
равна 2 (см. рис. 3). В прямо- |
|||||||||
угольном |
|
треугольнике ACD, |
где |
|||||||
ACD 90 , |
|
|
AD 2, |
находим |
AC |
|||||
|
|
|
|
|
|
|
|
|
||
22 12 |
|
|
|
|
. Из прямоугольного тре- |
|||||
|
|
3 |
||||||||
угольника |
|
ACC1 |
имеем |
AC1 |
||||||
|
|
|
|
ABC , |
||||||
( |
|
|
|
|
2. В треугольнике |
|||||
3)2 12 |
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
используя теорему косинусов, получаем
|
|
|
|
|
22 ( 2) |
2 12 |
5 2 |
|
|
|
|||||||||||
cos |
|
|
|
|
|
|
|
|
|
|
, |
||||||||||
|
|
|
|
|
|
|
8 |
||||||||||||||
2 2 |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
AC1B . |
|
Далее |
|
|
|
находим |
||||||||||||||
|
|
|
|
и из треугольника AC H вы- |
|||||||||||||||||
sin |
|
14 |
|||||||||||||||||||
|
|
|
|||||||||||||||||||
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
соту |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
AH AC sin 2 |
|
|
|
|
|
|
|
|
. |
||||||||||||
14 |
|
14 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
8 |
|
|
|
|
|
4 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
E1 |
D1 |
||||
F1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
A1 |
B1 |
C1 |
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
E |
D |
||||
|
|
|
|||||
F |
|
|
|
|
|
|
|
A |
|
|
C |
||||
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
Рис. 3 |
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
. |
|
|
|
14 |
||||
|
|
|
|
|
|
||
4
Пример 6. (МИОО, 2010). В тетра-
эдре ABCD, все ребра которого равны l, найти расстояние от точки A до прямой, проходящей через точку B и середину E ребра CD.
Решение. Так как все ребра ABCD равные правильные треугольники, то медианы BE и AE треугольников BDC и
18.02.2011 4
ADC (см. рис. 4) равны и BE AE 3. 2
Рассмотрим равнобедренный треугольник BEA и его высоты EM и AH. Выражая площадь треугольника двумя способами, получаем
S |
BEA |
|
1 |
AH BE |
1 |
|
EM AB, |
||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
получаем |
|
равенство |
|
AH BE EM AB. |
|||||||||||||||||||||||||||
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
2 |
||||||||||||
EM |
|
|
BE2 BM 2 |
|
|||||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|||||||||||||||
то получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
EM AB |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
. |
|||||||||||||||||
AH |
|
|
|
2 |
6 |
||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
BE |
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
||||||||||||
D
E
H



 C
C
B
M

A
Рис. 4
Ответ: 6 . 3
В некоторых задачах удобно использовать плоскость, проходящую через данную точку перпендикулярно данной прямой.
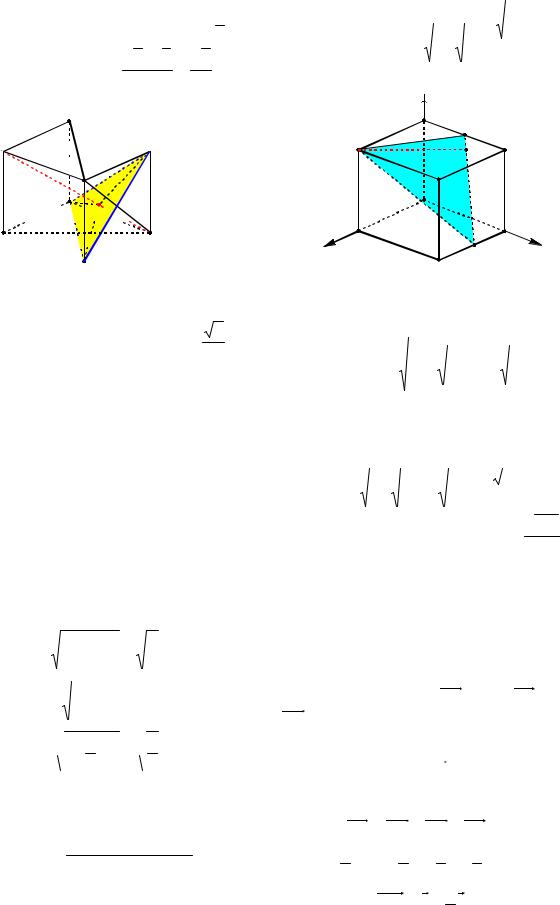
Пример 7. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки D до прямой A1C.
Решение. Пусть A1C BDC1 F (рис. 5). Так как A1C BDC1 (опорная задача
20), то FC1 FB FD как проекции на плоскость BDC1 равных наклонных CC1 , СВ и CD соответственно. Следовательно, точка F является центром правильного треугольника BDC1 . Поэтому искомое
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
расстояние равно радиусу окружности, описанной около треугольника BDC1 .
Сторона этого треугольника равна 
 2 ,
2 ,
значит, (D, A1C) DF 
 2
2 
 3
3 
 6 . 3 3
6 . 3 3
B1
A
 1
1 

 C1
C1
 D1
D1



 B
B

 F
F


A
 C
C
D
Рис. 5
Ответ: 6 . 3
координатный метод
Пример 8. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки D1 до прямой РQ, где Р и Q – сере-
дины соответственно ребер A1B1 и ВС.
Решение. Рассмотрим прямоугольную систему координат с началом в точке A (см. рис. 6). Найдем координаты точек
|
|
1 |
|
1 |
|
|
|
|
||
P |
0; |
|
;1 |
, Q |
|
;1; 0 |
|
, |
D (1;0;1). |
|
2 |
2 |
|||||||||
|
|
|
|
|
|
|
1 |
|||
Тогда
PQ |
1 |
|
|
1 |
1 |
|
3 |
, |
|||
4 |
|
2 |
|||||||||
|
4 |
|
|
|
|||||||
|
|
|
|
|
|
3 |
, |
||||
DQ |
|
|
1 |
1 1 |
|||||||
|
|
|
|
||||||||
1 |
|
4 |
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
||||
D1P 
 1 1 0
1 1 0 
 5 . 4 4
5 . 4 4
Из треугольника D1PQ , используя формулу
cos D1PQ D1P2 QP2 D1Q2 , 2 D1P QP
находим
|
5 |
|
3 |
|
9 |
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|||||||||||
|
4 |
|
|
|
4 |
|
|
|
|
|
|||||||
cos D PQ |
|
2 |
|
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
|
5 |
|
|
|
|
3 |
|
|
|
30 |
|
|
||
|
2 |
|
|
|
|
|
|
|
|
||||||||
4 |
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
z
D1 |
|
|
|
|
|
|
|
|
A1 |
|
P |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
B1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
A C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|||
x |
|
|
|
|
|
|
|
|
C |
|
Q |
|
|
|
|
|
|
|
y |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Рис. 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Далее получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
29 |
|
|
|
|||||||||||||
sin D PQ |
1 |
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
30 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пусть D1N PQ , где N PQ . Тогда |
||||||||||||||||||||||||||
D1N D1P sin D1PQ, |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
D N |
5 |
|
|
29 |
|
|
|
174 |
|
174 |
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
|
4 |
|
|
|
30 |
|
|
144 |
|
|
|
|
|
12 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Ответ: 
 174 . 12
174 . 12
векторный метод
Пример 9. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки D1 до прямой РQ, где Р и Q – сере-
дины соответственно ребер A1B1 и ВС.
Решение. |
Пусть |
AD a , |
AB b , |
AA1 c (см. |
рис. 6), |
тогда |a | |b | |
|
|c | 1, a b a c b c 0. |
|
||
Выразим вектор PQ через базисные |
|||
векторы a, b, |
c : |
|
|
PQ PB1 B1B BQ
1b c 1 a 1 a 1b c , 2 2 2 2
PD1 a 1b. 2
18.02.2011 |
5 |
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Пусть D1N PQ , |
где |
N PQ . Выра- |
|||||||||||||||||||||||||||||||||||||
зим вектор D1N , учитывая коллинеар- |
|||||||||||||||||||||||||||||||||||||||
ность векторов PN и PQ: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
D1N PN PD1 x PQ PD1 . |
|
||||||||||||||||||||||||||||||||||||
Так |
как D1N PQ, |
то |
|
D1N PQ 0. |
|||||||||||||||||||||||||||||||||||
Отсюда получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
(x PQ PD1) PQ 0, |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
PD1 |
PQ, |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x PQ |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 1 |
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
||||||||||||||||||||
x |
|
a |
|
|
|
|
b c |
|
|
a |
|
|
|
b |
|
|
|
|
a |
|
|
|
b |
c , |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|||||||||||
|
|
|
х |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
, |
|
х |
|
|
. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
6 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
D N |
1 |
PQ PD |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
b c |
|
|
|
|
|
b a |
|
|
||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
6 2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
11a 7 b 1c . 12 12 6
Длина вектора
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
7 |
|
|
1 |
2 |
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
D1N |
D1N |
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
c |
|
|||||||||||
12 |
|
12 |
6 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
121 |
|
|
49 |
|
|
1 |
|
|
|
174 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
144 |
144 |
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
174 |
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Замечание. Решение данного примера векторным методом не является рациональным, но приведено с целью показа широких возможностей векторного метода при решении задач разных видов.
18.02.2011 |
6 |
1.3.Расстояние от точки до плоскости
Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
Расстояние между двумя параллель-
ными плоскостями равно длине их общего перпендикуляра.
Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.
поэтапно-вычислительный метод
Расстояние от точки M до плоскости : 1) равно расстоянию до плоскости от произвольной точки P , лежащей на прямой l, которая проходит через точку
Mи параллельна плоскости ;
2)равно расстоянию до плоскости от произвольной точки P , лежащей на плоскости , которая проходит через
точку M и параллельна плоскости .
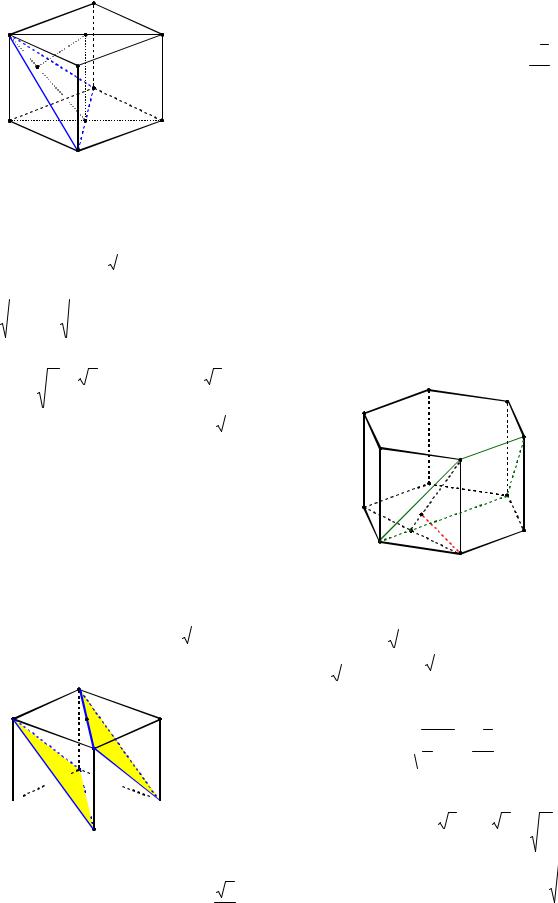
Пример 10. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки С1 до плоскости АВ1С .
Решение. Так как прямая А1С1 парал-
лельна АС, то прямая А1С1 параллельна плоскости АВ1С (см. рис. 7). Поэтому искомое расстояние h равно расстоянию от произвольной точки прямой А1С1 до плоскости АВ1С . Например, расстояние от центра О1 квадрата A1B1C1D1 до плос-
кости АВ1С равно h.
Пусть E – основание перпендикуляра, опущенного из точки О1 на прямую В1О, где O – центр квадрата ABCD. Прямая О1Е лежит в плоскости BB1D1D, а прямая АС перпендикулярна этой плоскости.
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
|
|
|
|
|
|
|
|
|
C1 |
|
|||||
B1 |
|
|
|
O1 |
|
|
|
|
D1 |
||||||
|
|
|
|
E |
A1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
B |
|
|
|
|
|
|
|
O |
|
|
|
|
D |
||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Рис. 7 |
|
|
|
|
|
||||
Поэтому О1Е АС и |
|
О1Е – перпенди- |
|||||||||||||
куляр к плоскости АВ1С , а О1Е h. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
Так |
как |
В О |
|
2 |
О О 1, то |
||||||||||
|
2 |
|
|||||||||||||
|
|
|
|
|
1 |
|
1 |
|
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
. Выражая двумя спо- |
||||||
ОВ |
1 |
1 |
|
3 |
|
||||||||||
|
|
||||||||||||||
1 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
собами площадь треугольника В1О1О,
получим h |
3 |
|
|
2 |
1, откуда h |
|
3 |
. |
|
|
||
|
2 |
|
3 |
|||||||||
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Ответ: |
|
|
3 |
|
. |
||
|
|
|
|
|
3 |
|
||||||
|
|
|
|
|
|
|
|
|
||||
Пример 11. В единичном кубе |
||||||||||||
ABCDA1B1C1D1 |
найти расстояние от |
|||||||||||
точки D до плоскости АВ1С . |
|
|
|
|
|
|
||||||
Решение. Так как плоскости DA1С1 и
АВ1С параллельны A1C1 ||AC, A1D||B1C
D DA1С1 и |
O1 DA1С1 |
(см. рис. 8), то |
|||||
получаем искомое расстояние |
|
|
|
|
|
||
(D, AB C) (O , AB C) |
|
|
|
. |
|||
3 |
|||||||
|
|
|
|||||
1 |
1 |
1 |
3 |
|
|
||
|
C1 |
|
|
|
|||
|
|
|
|
|
|
|
|
B1 |
O1 |
|
D1 |
||||
|
|
||||||
|
A1 |
|
|
|
|
|
|


 C
C



B










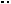











 D
D
A
Рис. 8
Ответ: 3 . 3
Замечание. Из данного примера следует, что расстояние между параллельными плоскостями DA1С1 и АВ1С равно
(DA1C1, AB1C) (D, AB1C) 
 3 . 3
3 . 3
Пример 12. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны l, найти расстояние от точкиA до плоскости A1B1С .
Решение. Прямая FC перпендикулярна АЕ и AA1, поэтому перпендикулярна плоскости AA1E1 (см. рис. 9). Пусть
FC AE G . Плоскость AA1E1 перпен-
дикулярна плоскости A1B1С , содержащей прямую FC, и пересекает ее по прямой A1G . Длина высоты AH в треугольнике
AA1G является искомым расстоянием.
|
|
|
D1 |
|
|
|
C1 |
||
|
E1 |
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
F1 |
|
|
|
|
B1 |
||
|
|
|
|
|
A1 |
||||
|
|
|
|
|
|
|
|
||
|
|
|
D |
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
E |
H |
|||||||
|
|
|
|
|
|
||||
|
|
|
G |
|
|
|
|
B |
|
|
|
F |
|
|
|
A |
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
Рис. 9 |
|||||
Так как в прямоугольном треугольнике |
|||||||||
ADE |
|
|
|
|
|
|
|
|
|
|
AE AD2 |
|
ED2 , то есть |
||||||
|
|
|
|
|
|
|
. Из прямоугольно- |
||
AE |
|
, то AG |
|
|
3 |
||||
3 |
|
||||||||
|
|
|
|
||||||
2
го треугольника AGA1 находим
GA1 
 3 1
3 1 
 7 . 4 2
7 . 4 2
Высота AH равна
|
AG AA |
|
3 |
|
7 |
3 |
|
|
|
|
|
||
AH |
1 |
|
|
1 |
: |
|
|
|
. |
|
|
||
GA |
2 |
|
|
||||||||||
|
|
|
2 |
7 |
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
3 |
. |
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
7 |
|
|
||||
18.02.2011 |
7 |
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
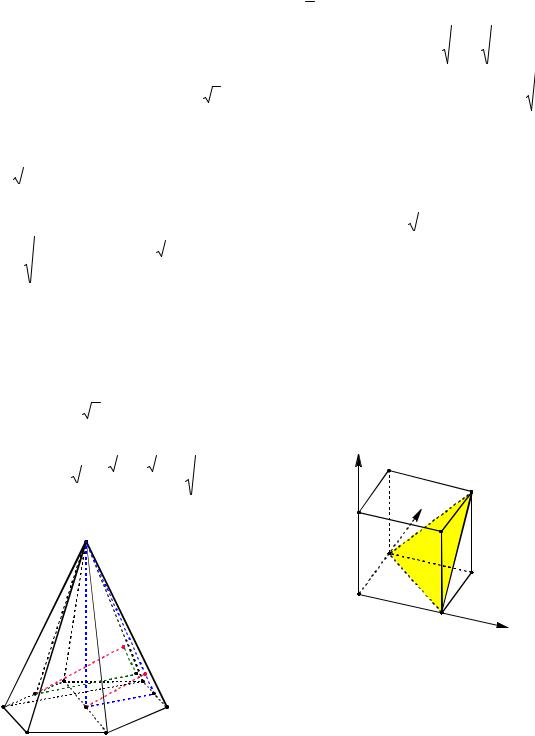
Пример 13. В правильной шестиугольной пирамиде MABCDEF, стороны основания которой равны 1, а боковые ребра равны 4, найти расстояние от середины ребра BC до плоскости грани EMD.
Решение. В правильном шестиуголь-
нике |
ABCDEF |
|
BD DE |
и |
BD 3. |
||||||||||
Точка O центр |
|
ABCDEF (см. рис. 10). |
|||||||||||||
Тогда |
MO высота пирамиды. Из пря- |
||||||||||||||
моугольного треугольника MOD получа- |
|||||||||||||||
ем MO |
|
|
. Апофему |
ML |
|
боковой |
|||||||||
15 |
|||||||||||||||
грани DME находим из прямоугольного |
|||||||||||||||
треугольника MDL |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DE 2 |
|
3 |
|
|
|
|
||
|
ML |
|
MD |
2 |
|
|
7 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
По |
признаку |
перпендикулярности |
|||||||||||||
плоскостей |
|
|
(DE MOL, |
|
|
поскольку |
|||||||||
DE MO |
и DE ML) |
MOL DME . |
|||||||||||||
Поэтому высота OH треугольника MOL перпендикулярна плоскости DME . Из прямоугольного треугольника MOL, в
котором OL |
BD |
|
3 |
, получаем |
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
MO OL |
|
|
|
|
|
|
|
: |
3 |
|
|
|
|
|
|
. |
||||
OH |
|
|
|
|
|
3 |
7 |
|
5 |
|
|||||||||||
15 |
|||||||||||||||||||||
|
|
|
|
|
|
|
7 |
||||||||||||||
|
ML |
|
|
|
|
2 2 |
|
|
|
|
|
||||||||||
M
|
|
|
Q |
|
||
L |
C |
K |
H |
|||
|
|
D |
||||
B |
|
|
O |
|
|
L E |
|
|
|
|
|
|
|
A |
|
|
F |
|
|
|
|
|
Рис. 10 |
|
|
|
|
Опустив из точки L перпендикуляры |
||||||
LQ на плоскость грани |
DME и LK на |
|||||
прямую DE , |
|
получим |
треугольник |
|||
LQK , подобный треугольнику OHD . |
||||||
Так как расстояние от точки L до прямой |
||||||
DE равно LK |
3 |
BD |
3 |
OL, то коэф- |
||
|
2 |
|||||
|
4 |
|
|
|
||
18.02.2011 |
|
|
|
|
|
8 |
фициент подобия этих треугольников ра-
вен 3 . Отсюда
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LQ |
3 |
OH |
3 |
|
|
|
5 |
|
|
|
45 |
|
. |
|
|
|
|
|||||||||
|
|
7 |
28 |
|||||||||||||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
45 |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
|
||||||||
координатный метод |
||||||||||||||||||||||||||
Расстояние от точки |
M до плоскости |
|||||||||||||||||||||||||
можно вычислить по формуле |
||||||||||||||||||||||||||
M, |
|
|
ax0 by0 cz0 d |
|
|
, |
||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
a2 b2 c2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где M x0 , y0 , z0 , |
плоскость |
|
задана |
|||||||||||||||||||||||
уравнением ax by cz d 0.
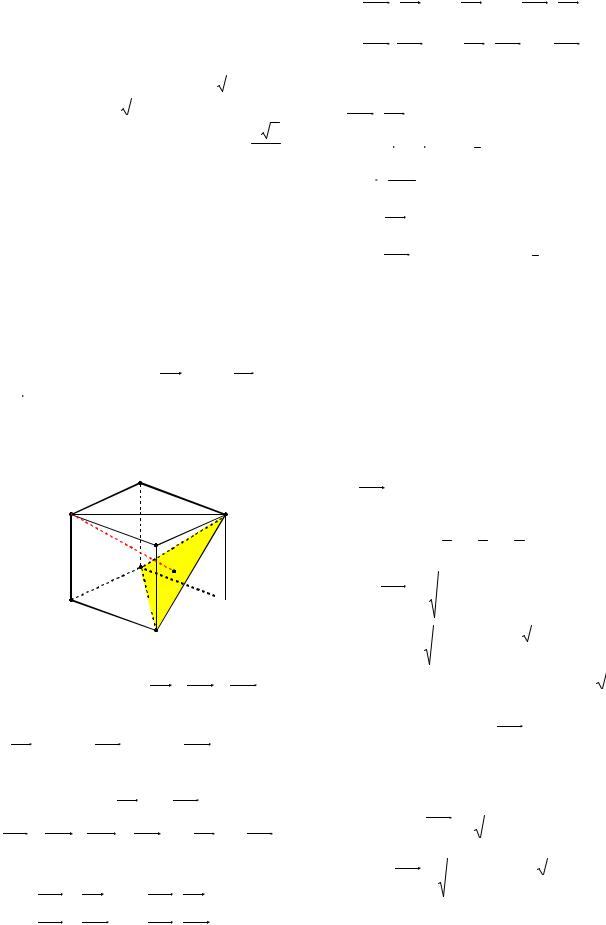
Пример 14. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки А1 до плоскости BDC1 .
Решение. Составим уравнение плоскости, проходящей через точки B(0;1;0),
D(1;0;0) и C1(1;1;1) (см. рис. 11).
z |
B1 |
|
|
A1 |
|
y |
C1 |
|
|
||
|
B |
D1 |
|
|
|
|
|
|
|
|
C |
A |
|
D |
|
|
|
x |
|
|
|
|
|
|
|
Рис. 11 |
|
Для этого подставим координаты этих точек в общее уравнение плоскости
ax by cz d 0.
Получим систему уравнений
b d 0, |
b d, |
|
|
a d 0, |
или a d, |
|
|
a b c d 0 |
c d |
Отсюда находим уравнение
dx dy dz d 0
или
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
x y z 1 0.
По формуле находим расстояние от точки А1(0;0;1) до плоскости BDC1:
|
0 0 1 1 |
|
|
|
|
|
||
А, |
|
2 3 |
. |
|||||
|
|
|
|
|||||
1 |
1 1 1 |
3 |
|
|
|
|||
|
|
|
|
|||||
Ответ: 2 3 . 3
Замечание. В разделе «Угол между плоскостями» более подробно рассмотрен вопрос о составлении уравнения плоскости, проходящей через три заданные точки.
векторный метод
Пример 15. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки А1 до плоскости BDC1 .
Решение.
AA1 c (см.
| c | 1, a b
A1
A
Пусть |
AD a , |
AB b , |
рис. 12), |
тогда |
|a | |b | |
a c b c 0. |
|
|
B1 |
|
|
D1 |
C1 |
|
|
||
B |
M |
|

 C
C
D
Рис. 12
Выразим векторы DB, DC1, C1A1 че-
рез базисные a, b, c :
DB b a, DC1 b c , C1A1 a b .
Пусть |
МА1 BDC1 , |
|
где |
M BDC1. |
|||
Вектор |
|
x DB y DC1 , поэтому |
|||||
C1M |
|||||||
MA1 C1A1 C1M C1A1 (x DB y DC1). |
|||||||
Далее имеем |
|
|
|
|
|||
MA DB, |
MA DB 0, |
||||||
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
DC1 |
0 |
|
MA1 DC1 |
MA1 |
||||||
18.02.2011 |
|
|
|
|
9 |
||
|
|
|
2 |
y DC |
|
0, |
C A |
DB x DB |
|
DB |
|||
|
1 1 |
|
|
1 |
|
|
C1A1 DC1 x DB DC1 y DC12 0.
Так как
C1A1 DB ( a b)(b a) a2 b2 0, DC1 DB (b c)(b a) b2 1, DC1 C1A1 (b c)( a b) b2 1, DB2 (b a)2 b2 a2 2,
DC12 (b c)2 b2 c2 2,
то имеем
0 (x 2 y 1) 0, |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
1 (x 1 y 2) 0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2x y 0, |
|
|
x |
|
|
|
|
, |
|
|||||
|
|
3 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x 2y 1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
y |
|
3 |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда получаем |
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
||
MA1 a b |
|
|
(b a) |
|
|
|
(b |
c) |
||||||
|
|
|
|
|
||||||||||
33
2a 2b 2c ,
|
|
|
|
3 |
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
MA1 |
|
|
|
|
|
|
a |
|
|
b |
|
|
|
c |
|
|
|
|
|
|
|
|
|
||||||||
|
3 |
3 |
3 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
4 |
|
4 |
|
4 |
|
|
|
|
|
3 |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
9 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание. Вектор MA1 |
в данном ба- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|
|
|||||||
зисе имеет координаты |
|
|
|
|
; |
|
; |
|
|
, по- |
||||||||||||||||||||||
|
3 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
||||||||
этому длину этого вектора можно найти
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по формуле |
MA |
|
|
a2 b2 |
c2 , то есть |
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
|
. |
|||
MA |
4 |
|
4 |
|
4 |
|
3 |
||||||||
9 |
|
|
|
|
|
||||||||||
1 |
|
|
9 |
9 |
|
|
|
3 |
|
|
|
|
|||
www.alexlarin.narod.ru
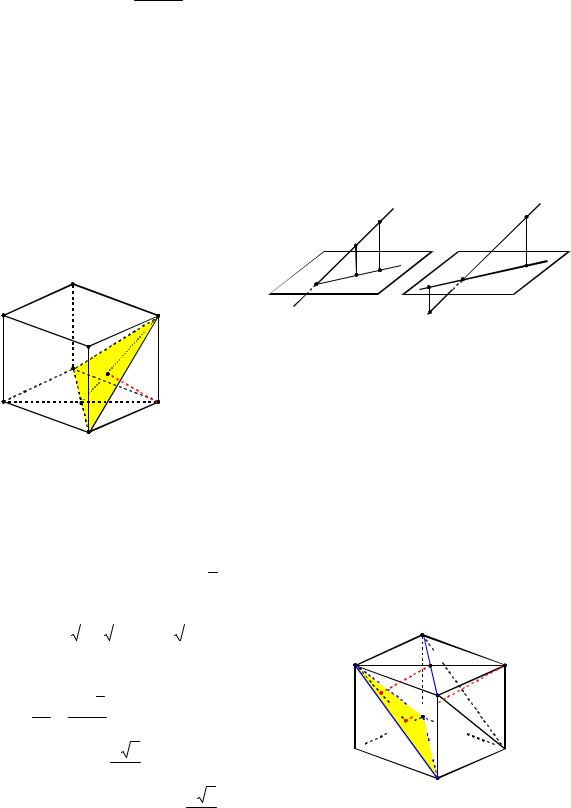
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
метод объемов
Если объем пирамиды АВСМ равен VABCM , то расстояние от точки M до
плоскости , содержащей треугольник АВС, вычисляют по формуле
M, M, ABC 3VABCM .
SABC
В общем случае рассматривают равенство объемов одной фигуры, выраженные двумя независимыми способами.
Пример |
16. |
Ребро |
куба |
ABCDA1B1C1D1 |
равно а. Найти расстоя- |
||
ние от точки C до плоскости BDC1 .
Решение. Искомое расстояние x равно высоте CQ (см. рис. 13), опущенной в
пирамиде |
BCDC1 |
из вершины C на ос- |
|||||||||||||
нование BDC1 . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
B Q |
|
|
|
|||
|
|
|
A |
|
|
|
|
|
R |
C |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 13 |
|
|
|
|
||
|
Объем этой пирамиды равен |
|
|
|
|||||||||||
1 |
S |
|
CC |
|
|
1 |
|
1 |
BC |
CD CC |
|
a3 |
|||
|
|
BCD |
|
|
|
|
. |
||||||||
3 |
|
3 |
2 |
|
|||||||||||
|
|
|
1 |
|
|
|
1 |
6 |
|
||||||
С другой стороны, так как треугольник
BDC1 равносторонний со стороной а
 2, объем пирамиды равен
2, объем пирамиды равен
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
SBC D CQ |
1 |
|
(a |
2)2 3 |
|
x |
a2 |
3 |
|
x. |
||
3 |
3 |
|
4 |
|
|
6 |
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|||||
Отсюда получаем уравнение
a3 a2 
 3 x, 6 6
3 x, 6 6
из которого находим x a 3 . 3
Ответ: a 3 . 3
18.02.2011 |
10 |
метод опорных задач
Применение данного метода состоит в применении известных опорных задач, которые в большинстве случаев формулируются как теоремы.
●Расстояние от точки M до плоскости
можно вычислить по формуле
|
|
|
r |
, |
|
|
|
|
|
|
|||
|
|
|
1 r |
|
||
|
|
|
1 |
|
|
|
где M, , |
1 M1, , |
OM r, |
||||
OM1 r1, |
MM1 O; в частности, |
|||||
1 , если r r1 |
(прямая m, проходя- |
|||||
щая через точку |
M , пересекает плос- |
|||||
кость в точке O, а точка М1 лежит на |
||||||
прямой m (см. рис. 14а и 14б)). |
|
|||||
|
M |
|
|
|
M |
|
|
M1 |
|
|
|
m |
|
m |
|
|
|
|
A |
|
O |
A1 |
A |
|
A1 O |
||
|
|
|
|
|
||
а |
|
|
|
M1 |
|
|
|
|
|
|
б |
|
|
|
|
Рис. 14 |
|
|||
Пример 17. В единичном кубе |
||||||
ABCDA1B1C1D1 |
найти расстояние от |
|||||
точки D1 |
до плоскости АВ1С . |
|
||||
Решение. Используем найденное расстояние (пример 10) от точки С1 (от точ-
ки O1 ) до плоскости |
АВ1С . Опустим |
||||
перпендикуляр D1F на прямую B1E (см. |
|||||
рис. 15). Тогда имеем |
|
|
|
|
|
(D , ABC) (O , ABC) |
B1D1 |
, |
|||
|
|||||
1 1 |
1 |
1 |
BO |
||
|
|
|
1 |
1 |
|
|
C1 |
|
|
|
|
B1 |
|
O1 |
|
D1 |
|
E |
|
A1 |
|
||
|
|
|
|
||

 F
F





 C
C



B





















 D
D
A
Рис. 15
www.alexlarin.narod.ru
