
ЕГЭ / Математика / МАТЕМАТИКА ЕГЭ 2011 (типовые задания С4)
.pdf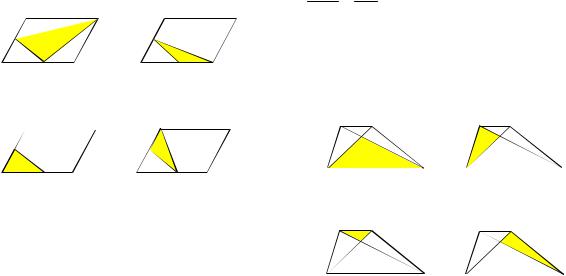
Корянов А.Г., Прокофьев А.А.
8S S 2S 2S 3S .
B C A B E  E
E
A F D D F C
аб
D A C D E E
C F B B F A
вг
Рис. 34
В остальных случаях искомая площадь будет равна S .
Ответ: S или 3S .
Пример 31. Диагонали АС и BD трапеции ABCD пересекаются в точке Е. Найдите площадь трапеции, если площадь треугольника AED равна 9, а точка
Еделит одну из диагоналей в отношении
1:3.
● Трапеция разбивается диагоналями на два равновеликих треугольника (примыкающих к боковым сторонам) и два подобных треугольника (примыкающих к основаниям).
Если у двух треугольников равны высоты, то их площади относятся как основания.
Решение. При решении данной задачи неоднозначность в условии, как и в предыдущем примере, состоит в выборе варианта буквенного обозначения вершин трапеции и дополнительно к этому в выборе большего основания. Пусть точка Е делит диагональ в отношении 1:3, считая от вершины верхнего основания.
1. Рассмотрим трапецию с основаниями ВС и AD (см. рис. 35а). Треугольники ВЕС и АED подобны (по двум углам) с
коэффициентом |
подобия k |
EC |
|
1 |
. |
||||
|
|
||||||||
|
|
|
SAED |
|
|
AE |
3 |
||
Значит, |
|
|
32 9. |
Отсюда |
|||||
|
SBEC |
|
|||||||
|
|
|
|
|
|
|
|
|
|
SBEC |
SAED |
1. Треугольники |
АВE |
и |
|||||
|
|||||||||
9 |
|
|
|
|
|
|
|
|
|
05.01.2011.
ВЕС имеют общую высоту, поэтому
SABE AE 3 и SABE 3 SBEC 3. Ана-
SBEC EC
логично SDEC 3 SBEC 3.
Следовательно, искомая площадь рав-
на SABCD 1 3 3 9 16.
B |
1 |
C |
A |
3 |
B |
|
3 |
3 |
9 |
9 |
|||
E |
E |
|||||
|
9 |
|
27 |
|||
A D D
D D C
C
аб
D |
A |
C |
3 |
D |
9 |
27 |
9 |
9 |
|
27 E |
E |
81 27
CB B A
A
вг
Рис. 35
2. В остальных случаях, решая аналогичным образом, получим
SABCD 3 9 9 27 48 (см. рис. 35б и
рис. 35г);
SABCD 9 27 27 81 144 (см. рис. 35в).
Ответ: 16; 48; 144.
выбор линейного элемента
Пример 32. Площадь треугольника ABCравна 8. MN – средняя линия. Найдите площадь треугольника CMN .
● Прямая, параллельная стороне треугольника и пересекающая две другие, отсекает от него треугольник, подобный данному.
Решение. При решении данной задачи неоднозначность состоит в выборе средней линии. Рассмотрим три случая (см.
рис. 36).
1. Отрезок MN параллелен отрезку ВС (см. рис. 36а). Так как CN – медиана треугольника АВС, то
S |
ANC |
|
1 |
S |
ABC |
|
1 |
8 4. |
|
|
|||||||
|
2 |
|
2 |
|
||||
MN – медиана треугольника АMС, поэтому
S |
CMN |
|
1 |
S |
AMC |
|
1 |
4 2. |
|
|
|||||||
|
2 |
|
2 |
|
||||
21
Корянов А.Г., Прокофьев А.А. |
|
|||
|
B |
|
B |
B |
N |
|
M |
N |
N |
A |
M C |
A |
C |
A M C |
|
а |
|
б |
в |
Рис. 36
2.Отрезок MN параллелен отрезку АС (см. рис. 36б). В этом случае решение аналогично предыдущему.
3.Отрезок MN параллелен отрезку АВ (см. рис. 36в). Треугольники CMN и АВС подобны. Тогда
|
|
1 |
2 |
|
1 |
|
|
SCMN |
|
|
|
SABC |
|
|
8 2. |
|
4 |
||||||
|
|
2 |
|
|
|
||
Ответ: 2.
выбор углового элемента
Пример 33. Треугольник ABC вписан в окружность радиуса 12. Известно, что AB 6 и BC 4. Найдите АС.
Решение. 1-й способ. Используя обобщенную теорему синусов, найдем
sin A |
|
BC |
|
4 |
|
|
1 |
, |
|||
|
|
|
2 12 |
6 |
|||||||
|
|
2R |
|
|
|
||||||
sinC |
AB |
|
|
6 |
|
|
|
1 |
. |
||
|
|
2 12 |
|
4 |
|||||||
|
|
2R |
|
|
|
||||||
Так как B 180 A C , то sin B sin(180 A C)
sin( A C).
1.Если треугольник АВС – остроугольный, то
cos A 
 35, cos C
35, cos C 
 15. 6 4
15. 6 4
Используя формулу синуса суммы, получим
sin B sin( A C)
|
1 |
|
15 |
|
35 |
|
1 |
|
35 15 |
. |
|
4 |
6 |
|
24 |
||||||
6 |
|
|
4 |
|
|
|||||
Тогда можем найти искомую величину
AC 2Rsin B
|
24 |
|
35 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
35 |
15. |
|
|
||||||||||||||||||||||
|
|
24 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. Пусть угол С – тупой, тогда |
|
|
|
|
||||||||||||||||||||||
|
|
sin B sin( A C) |
|
|
|
|
||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
15 |
35 |
|
|
|
35 |
15 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
6 |
|
4 |
|
|
6 |
|
4 |
24 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
05.01.2011.
Отсюда AC 
 35
35 
 15.
15.
3. Случай, когда угол А – тупой, невозможен.
2-й способ. Используем теорему коси-
нусов AC2 AB2 BC2 2AB BCcosB
и следствие |
из теоремы синусов |
AC 2Rsin B. |
Отсюда получаем триго- |
нометрическое уравнение
576sin2 B 36 16 48cosB.
Решая последнее уравнение, находим
cosB 1 5 21 . Положительное значе-
24
ние косинуса соответствует острому углу В, отрицательное – тупому. Зная значение
sin B 
 50 10
50 10
 21
21 
 35
35 
 15 , 24 24
15 , 24 24
находим AC 
 35
35 
 15 .
15 .
Ответ: 
 35
35 
 15 .
15 .
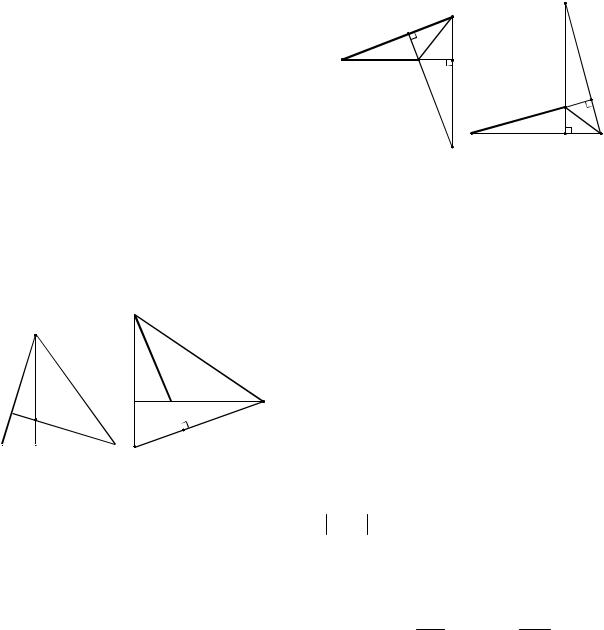
Пример 34. Высоты треугольника ABC пересекаются в точке Н. Известно, что CH AB. Найдите угол АСВ.
C |
C |
|
|
|
|
|
|
|
|
F |
|
|
F |
A |
|
E |
E |
B |
|
H |
|
|
|
|
D |
|
|
A D |
B H |
|
|
б |
|
||
а |
|
|
|
|
Рис. 37 |
|
|
Решение. 1. Пусть треугольник |
|||
ABC остроугольный |
(см. рис. 37а). |
||
Пусть ВЕ и CD – высоты треугольника. |
|||
Углы АВЕ и HCE равны, как углы с соот- |
|||
ветственно |
перпендикулярными |
сторо- |
|
нами. Треугольники АЕВ и HEC равны по |
|||
гипотенузе (CH AB) и острому углу. |
|||
Отсюда |
AE EH, |
и |
значит, |
EAH AHE 45 . |
В прямоугольном |
||
треугольнике ACF имеем CAF 45 , поэтому ACF 45 .
Остальные случаи рассмотрите самостоятельно.
2.Угол ВАС – тупой (см. рис. 37б).
3.Угол АВС – тупой.
22
Корянов А.Г., Прокофьев А.А.
4.Угол АСВ – тупой.
5.Угол АВС – прямой.
6.Угол ВАС – прямой.
7.Случай, когда угол АСВ – прямой, невозможен (почему?).
Ответ: 45 или 135 .
Опорная задача. Если Н – ортоцентр треугольника, то радиусы окружностей, описанных около треугольников АВС, АВН, ВСН, АСН, равны между собой.
Доказательство. Так как в четырех-
угольнике AEHD углы E и D прямые (см. рис. 38а), то A DHE 180 . Отсюда получаем BHC DHE 180 A. Радиус окружности, описанной около треугольника ВНС, равен
BC |
|
BC |
|
a |
. |
2sin(180 A) |
2sin A |
|
|||
|
|
2sin |
|||
Отсюда следует, что радиусы окружностей, описанных около треугольников АВС и ВСН равны между собой. Аналогичное доказательство проводят и для других треугольников.
Пример 35. Высоты треугольника АВС пересекаются в точке Н. Известно, что отрезок СН равен радиусу окружности, описанной около треугольника. Найдите угол АСВ.
C 
C
E
 H E
H E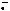
 A
A  B
B




 D A D B
D A D B  H
H
а б
Рис. 38
Решение. Пусть R – радиус окружности, описанной около треугольника ABC. Так как радиусы окружностей, описанных около треугольников ABC и BCH равны между собой, то для треугольника BCH имеем
CH 2Rsin HBC
или
R 2Rsin HBC .
|
|
|
05.01.2011. |
Отсюда |
sin HBC |
1 |
. Значит, |
|
|||
|
2 |
|
|
HBC 30 или HBC 150 .
1.Если треугольник ABC – остроугольный, то из треугольника BEC на-
ходим C 90 30 60 (см. рис. 38а).
2. Если в треугольнике ABC угол A – тупой, то HBC 30 (в треугольнике DBC угол D прямой, а угол DBC может быть только острым). Из треугольни-
ка DBC |
находим C 90 30 60 |
||||
(см. рис. 38б). |
|
|
|
|
|
|
E |
C |
|
H |
|
|
|
|
|
|
|
A |
B |
D |
|
|
|
|
|
|
|
D |
|
|
|
|
|
C |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
H |
|
E |
B |
|
|
в |
Рис. 38 |
|
г |
|
|
|
|
|
|
|
3. Если в треугольнике ABC угол B – |
|||||
тупой, то |
HBC 150 |
(почему |
этот |
||
угол тупой?) и |
CBE 30 . |
Из |
тре- |
||
угольника |
CBE |
(см. рис. |
38в) |
находим |
|
C 90 30 60 .
4.Если в треугольнике АВС угол С – тупой (см. рис. 38г), то HBC 30 (по-
чему этот угол острый?). Из треугольника СВD находим BCD 90 30 60 .
Тогда ACB 180 60 120 .
Ответ: 60 или 120 .
Опорная задача. Пусть в треугольнике АВС проведены высоты AA1 и CC1.
Тогда треугольник A1BC1 подобен данному с коэффициентом подобия, равным cosB .
Доказательство. Рассмотрим остроугольный треугольник (см. рис. 39а). Для прямоугольных треугольников BA1A и
BC1C имеем BA1 cosB и BC1 cosB AB BC
соответственно. Следовательно треугольники BA1C1 и BACподобны (второй
23
Корянов А.Г., Прокофьев А.А.
признак), так как имеют общий угол В и
BA1 BC1 cosB. AB BC
A |
|
|
B1 |
C1 |
|
H |
|
B A1 |
C |
Рис. 39а
Случай тупого угла В рассмотрите самостоятельно
Пример 36. Точки A1, B1, C 1 – основания высот треугольника ABC. Углы
треугольника A1B1C1 равны 90°, 60° и |
|
30°. Найдите углы треугольника ABC. |
|
Решение. 1. Треугольник АВС – ост- |
|
роугольный (см. рис. 39а). |
|
Так как треугольник |
BC1A1 подобен |
треугольнику АВС, то |
BC1A1 BCA. |
Аналогично из подобия треугольников
AB1C1 |
и АВС имеем AC1B1 BCA. |
|
Далее развернутый угол при вершине C1 |
||
составлен из суммы углов BC1A1 , |
AC1B1 |
|
и B1C1A1 . Отсюда получаем соотноше- |
||
ние |
2 C B1C1 A1 180 |
или |
1
C 90 2 B1C1A1 .
H
A1 B1
B1
C
A |
C1 |
B |
|
Рис. 39б |
|
Такие же равенства можно получить для других острых углов. Используем
|
|
|
|
05.01.2011. |
данные |
углы: |
90 |
1 |
90 45 , |
|
||||
|
|
2 |
|
|
90 1 60 60 , 90 1 30 75 . 2 2
Остальные случаи рассмотрите самостоятельно.
2.Угол АСВ – тупой (см. рис. 39б).
3.Угол АВС – тупой.
4.Угол ВАС – тупой.
Случаи, когда один из углов АВС, ВАС, АСВ – прямой, невозможны (поче-
му?).
Замечание. Другое решение может быть основано на следующей опорной задаче:
Высоты остроугольного треугольника являются биссектрисами его ортотреугольника (треугольник, образованный основаниями высот). (докажите)
Ответ: 45°, 75°, 60° или 135°, 15°, 30° или 120°, 15°, 45° или 105°, 30°, 45°.
выбор кругового элемента (дуги)
Рассмотрим задачу, в которой имеются две точки, делящие окружность на две дуги, но не указано, какой из этих двух дуг касается другая окружность.
Пример 37. Окружности с центрами О и В радиуса ОВ пересекаются в точке С. Радиус ОА окружности с центром О перпендикулярен ОВ, причем точки А и С лежат по одну сторону от прямой ОВ. Окружность S1 касается меньших дуг АВ и ОС этих окружностей, а также прямой ОА, а окружность S2 касается окружности с центром В, прямой ОА и окружности S1. Найдите отношение радиуса окружности S1 к радиусу ок-
ружности S2 .
Решение. Так как окружность S1 радиуса а и окружность с центром в точке В и радиуса R касаются друг друга и общей прямой ОА, то имеем OI 2
 Ra (расстояние между точками касания окружностей общей касательной), OK R a.
Ra (расстояние между точками касания окружностей общей касательной), OK R a.
Далее используем теорему Пифагора в треугольнике OKI:
24
Корянов А.Г., Прокофьев А.А.
(R a)2 a2 2
 Ra 2 .
Ra 2 .
Отсюда получаем R 6a. Рассмотрим первый случай касания
окружности S2 радиуса b (см. рис. 40а).
A








 C
C 


I 
 a
a 
 K
K 





J 
 Eb
Eb





 O R B
O R B
Рис. 40а
Тогда OI OJ JI, или
2
 aR 2
aR 2
 bR 2
bR 2
 ab,
ab,
откуда 
 6a2
6a2 
 6ab
6ab 
 ab,
ab,
a |
|
6 |
1 |
, |
a |
|
7 2 6 |
. |
|
|
|
|
|
|
|
||||
b |
6 |
|
|
b |
6 |
|
|||
J b E
b E
A 

I

 a K
a K


 C
C





 O R
O R  B
B
Рис. 40б
Для второго случая (см. рис. 40б) име-
ем OJ OI IJ,
2
 bR 2
bR 2
 aR 2
aR 2
 ab .
ab .
Проводя вычисления аналогично предыдущему случаю, получим
a7 2
 6 .
6 .
b6
05.01.2011.
Ответ: 7 2 6 . 6
выбор плоской фигуры
Пример 38. Основания трапеции равны a и b. Прямая, параллельная основаниям, разбивает трапецию на две трапеции, площади которых относятся как 2:3. Найдите длину отрезка этой прямой, заключенного внутри трапеции.
B |
|
b |
x b |
|
|
C |
H |
E |
|
x |
F |
|
|
||
E1 |
|
|
F1 |
x |
|
P a xD |
|
A |
a |
||
|
|
|
|
Рис. 41
Решение. 1-й способ. Обозначим искомый отрезок EF через x (см. рис. 41).
1. Пусть площади трапеций BCFE и AEFD относятся как 2:3:
|
SBCFE |
|
|
|
b x |
h |
2 |
|
|||||
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
1 |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
SAEFD |
|
a x |
|
|
||||||||
|
|
|
|
|
3 |
|
|||||||
|
|
|
|
|
|
|
|
h2 |
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда |
h1 |
|
2(a x) |
, |
|
(*) |
|
||||||
|
|
|
|
||||||||||
|
|
h2 |
|
3(b x) |
|
|
|
|
|||||
где h1 и h2 высоты этих трапеций. Через точку F проведем отрезок PH
параллельно AB . Тогда треугольники PFD и CHF подобны (докажите) и
CH |
|
h1 |
, |
x b |
|
h1 |
. |
|
|
|
|||||
|
|
|
|
||||
BP h2 |
a x h2 |
||||||
Используем соотношение (*):
x b |
|
2(a x) |
. |
a x |
|
||
|
3(b x) |
||
Решая полученное уравнение относительно переменной x, получаем
3 x2 b2 2 a2 x2 ,
5x2 2a2 3b2 ,
x |
2a2 |
3b2 |
|
|
|
. |
|
|
5 |
||
|
|
|
|
25
Корянов А.Г., Прокофьев А.А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2-й способ. Обозначим SBCFE S1 , |
|
|
|
||||||||||||||||||||||||||||||||||||
SAEFD S2 , тогда S2 |
|
1,5S1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
b C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
x |
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 42 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Достроим трапецию ABCD до тре- |
|
|
|
||||||||||||||||||||||||||||||||||||
угольника AHD (см. рис. 42) и обозна- |
|
|
||||||||||||||||||||||||||||||||||||||
чим SBHC S. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Так как треугольники AHD и BHC |
|
|
|
||||||||||||||||||||||||||||||||||||
подобны (докажите), то имеем |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
S |
|
|
|
|
|
x 2 |
|
|
|
|
S S S |
2 |
|
|
a2 |
. ( |
|
|
|
||||||||||||||||||||
|
|
|
EHF |
|
|
|
|
|
|
|
или |
|
1 |
|
|
|
|
|
|
|
|
|
) |
|
||||||||||||||||
|
SBHC |
|
|
b |
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
b2 |
|
|
|
* |
|
|
|||||||||||
|
Так как треугольники EHF и AHD |
|
|
|
||||||||||||||||||||||||||||||||||||
подобны (докажите), то имеем |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
S |
EHF |
|
|
|
x |
2 |
|
S S |
1 |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
. |
|
( |
|
) |
|
|
||||||||||||||
|
|
SAHD |
|
|
|
|
b |
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
** |
|
|
|||||||||
|
Из соотношений (*) и (**) имеем |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
S S |
|
|
a2 |
|
и 1 |
S |
1 |
|
|
|
|
x2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
S |
|
|
|
b2 |
|
|
S |
|
|
b2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
S S |
2 |
|
|
a2 b2 |
|
|
|
|
S |
1 |
|
x2 b |
2 |
|
||||||||||||||||||||
Далее |
1 |
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
b2 |
|
|
|
|
S |
|
|
|
|
|
b2 |
|
|
|
|||||||||||
Разделив одно равенство на другое, по-
|
S S |
2 |
|
a2 |
b2 |
. |
лучим |
1 |
|
|
|||
S |
|
x2 |
b2 |
|||
|
|
|
|
|||
1 |
|
|
|
|
|
|
С учетом соотношения S2 1,5S1 имеем уравнение относительно переменной
|
a2 |
b2 |
5 |
|
откуда x |
2a2 |
3b2 |
||
x: |
|
|
|
|
, |
|
|
. |
|
|
x2 |
b2 |
2 |
|
|
|
5 |
|
|
2. |
Случай, |
|
когда площади |
трапеций |
|||||
AEFD и BCFE относятся как 2:3, рассмотрите самостоятельно. В этом случае площади трапеций BCFE и AEFD относятся как 3:2.
|
2a2 |
3b2 |
|
3a2 |
2b2 |
|
Ответ: |
|
|
или |
|
|
. |
|
5 |
|
5 |
|||
|
|
|
|
|
||
05.01.2011.
5. Соответствие между множеством фигур и множеством их свойств
В задачах этого типа фигурируют объекты, которым приписываются определенные свойства, но не указан порядок соответствия между множеством объектов и множеством их свойств.
неопределенность между значением синуса (косинуса) угла и видом угла
Пример 39. Площадь треугольника равна 12. Две его стороны равны 6 и 8. Найдите угол между этими сторонами.
Решение. Используя формулу
S |
|
1 |
absin , получаем |
sin |
1 |
. Зна- |
|
|
|||||
|
2 |
|
2 |
|
||
чит 30 или 150 .
Ответ: 30 или 150 .
Пример 40. Радиус окружности равен 1. Найдите величину вписанного угла,
опирающегося на хорду, равную 
 2 . Ответ дайте в градусах.
2 . Ответ дайте в градусах.
B




 A1
A1
O
A
С 









Рис. 43
Решение. Хорда BC разбивает окружность на две дуги. Все вписанные углы, опирающиеся на эту хорду, с вершинами, лежащими на одной дуге, будут равны. Для любой точки A (см. рис. 43),
используя |
формулу sin A |
a |
, |
где |
|||||||
|
|||||||||||
|
|
|
|
|
2R |
|
|
|
|
||
a |
|
и |
R 1, |
получим sin A |
|
2 |
|
. |
|||
2 |
|||||||||||
2 |
|
||||||||||
Значит A1 |
45 |
или A 135 . |
|
|
|||||||
|
|
|
|
||||||||
|
|
|
|
Ответ: 45 или 135 . |
|||||||
Пример 41. Около треугольника ABC описана окружность с центром О, угол АОС равен 60°. В треугольник ABC вписана окружность с центром М. Найдите угол АМС.
26
Корянов А.Г., Прокофьев А.А.
Решение. В равнобедренном треугольнике АOС (OC OA R ) угол при вершине равен 60 . Следовательно, треугольник АOС – равносторонний и
AC R .
Используя следствие обобщенной теоремы синусов, получаем
AC 2Rsin B, R 2Rsin B, sin B 1.
|
2 |
Отсюда B 30 |
или B 150 . |
1. Пусть B 30 |
(см. рис. 44), тогда |
A C 150 . Центр вписанной окружности М, лежит на пересечении бис-
сектрис |
треугольника, |
значит |
MAC MCA 150 :2 75 . |
Тогда |
|
AMC 180 75 105 . |
|
|
B
O
 M
M 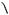
A |
B1 |
C |
|
|
Рис. 44 |
|
|
2. Случай, когда B1 |
150 |
(см. рис. |
|
44), рассмотрите самостоятельно. |
|||
|
Ответ: 165 |
или 105 . |
|
Пример 42. Медиана ВМ треугольника АВС равна его высоте АН. Найдите угол МВС.
B

 H
H
A M C
Рис. 45а
Решение. Пусть MBC . Найдем площадь треугольника АВС двумя способами. Так как медиана ВМ треугольника АВС разбивает его на два равновеликих треугольника, то
05.01.2011.
SABC 2SCBM 2 1 BC BM sin
2
BC BM sin .
1
С другой стороны, SABC 2 BC AH.
Учитывая, что AH BM, приравняем
площади BC BM sin 1 BC AH. По-
2
лучаем, что sin 0,5. Отсюда 30
(см. рис. 45а) или 150 (см. рис. 45б).
H
B
A M C
Рис. 45б
Ответ: 30 или 150 .
Пример 43. Трапеция ABCD с основаниями AD и ВС вписана в окружность с центром О. Найдите высоту трапеции, если ее средняя линия равна 3 и
sin AOB 3. 5
● Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали — полусумме оснований (средней линии). (докажите)
Вписанный угол измеряется половиной дуги, на которую он опирается.
B C
A

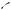
 H
H  D
D

 O
O
A1


 H1
H1 
 D1
D1
Рис. 46
Решение. Пусть AOB (см. рис. 46). Проведем высоту BH и диагональ BD. Отрезок HD равен средней линии. Так как вписанный угол BDA в два раза меньше центрального угла AOB, то
ADB . Из прямоугольного тре-
2
27
Корянов А.Г., Прокофьев А.А.
угольника BHD найдем высоту
BH HD tg |
|
. |
Используем |
формулу |
|||||||||||||
|
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тангенса |
половинного |
|
|
|
угла |
||||||||||||
tg |
|
|
sin |
. |
Тогда BH |
|
|
3sin |
. |
||||||||
|
|
|
|
|
|
|
|||||||||||
2 |
|
1 cos |
|
|
|
1 cos |
|||||||||||
1. |
Рассмотрим случай, |
когда |
|||||||||||||||
AOB – острый. Находим |
|
|
|||||||||||||||
|
|
|
|
|
|
|
4 |
|
3 |
3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
cos |
и BH |
5 |
|
|
1. |
|||||||||
|
|
|
|
4 |
|
||||||||||||
|
|
|
5 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
||||
2. Второй случай, когда AOB – тупой, рассмотрите самостоятельно.
3. Что будет в случае, когда
AOB 90 ?
Ответ: 9 или 1.
Опорная задача. Пусть О – центр окружности, вписанной в треугольник АВС. Докажите равенства:
|
C |
|
|
|
|
|
АОС |
|
В |
90 ; |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
АОВ |
С |
90 ; |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
A1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
O |
|
|
|
|
|
СОВ |
А |
90 . |
|||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
B |
C1 |
|
A |
|
|
|
|
Доказательство. |
|||||||||
|
|
|
|
Докажем |
|
|
|
первое |
|||||||||
|
Рис. 47 |
|
|
|
соотношение. |
Из |
|||||||||||
|
|
|
|
|
|
|
треугольника |
АОС |
|||||||||
имеем CАА |
A |
и |
АCО |
C |
. То- |
||||||||||||
|
|
2 |
|
|
A |
C |
2 |
|
|
|
|||||||
гда АОC |
|
|
|
|
|
|
|
|
|
|
|||||||
180 |
|
|
|
|
|
|
180 |
||||||||||
2 |
|
||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
A C 180 180 B B 90 .
2 |
2 |
2 |
Остальные равенства доказывают аналогично.
Пример 44. В треугольнике ABC проведены высоты ВМ и CN, О – центр вписанной окружности. Известно, что BC 24, MN 12 . Найдите радиус окружности, описанной около треугольника ВОС.
Решение. 1. Треугольник AMN подобен треугольнику АВС с коэффициентом
05.01.2011.
подобия k MN 12 1 cosA . От-
BC 24 2
сюда A 60 или A 120 .
B
B

 O
O
N O
O


 A
A 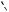 A M C M C
A M C M C
N
а б
Рис. 48
Используем соотношение СОВ
А 90 (см. опорную задачу). Значит
2 |
|
|
|
|
|
|
|
|
|
|
60 |
|
|
3 |
|
|
|
|
|
||
sin СОВ sin |
|
90 |
|
|
|
(см. рис. |
||||
|
2 |
|
||||||||
2 |
|
|
|
|
|
|
||||
|
|
120 |
|
|
1 |
|
||||
48а) или sin СОВ sin |
|
|
|
|
90 |
|
|
|
||
|
2 |
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|||
(см. рис. 48б).
Используем следствие из обобщенной теоремы синусов:
|
|
|
|
R |
BC |
|||||
|
|
|
|
|
|
. |
||||
|
|
|
||||||||
|
|
|
|
|
|
|
2sin COB |
|||
Отсюда получаем |
||||||||||
R |
24 |
|
8 |
|
|
или R |
24 |
24. |
||
|
3 |
|||||||||
|
|
|
|
|
||||||
|
3 |
|
|
|
|
1 |
|
|
||
Ответ: 8
 3 или 24.
3 или 24.
интерпретация алгебраического решения
Пример 45. Дана окружность радиуса 13. Точка М – середина радиуса ОК. Хорда АС перпендикулярна радиусу ОК. Найти расстояние ВМ, если известно, что AB BK 4 (рис. 49).
Решение. Обозначим BM через x (см. рис. 49а), тогда имеем OB 6,5 x и
AB 
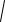 169 (6,5 x)2 , BK 6,5 x. Ис-
169 (6,5 x)2 , BK 6,5 x. Ис-
пользуя теорему Пифагора для треугольника AOB, получаем уравнение

 169 (6,5 x)2 10,5 x.
169 (6,5 x)2 10,5 x.
Отсюда находим корни x1 1,5 и x2 5,5.
28
Корянов А.Г., Прокофьев А.А.
O 
 O
O
 B
B 



 C
C  M
M
A

 M
M 




 B
B


 K
K


 A
A



 K
K



 C
C
а б
Рис. 49 Интерпретируем отрицательный ко-
рень: точка B расположена между точками M и K , то есть отрезок MB откладывается в противоположном направлении (см. рис. 49б). Оба корня удовлетворяют решению задачи.
Ответ: 1,5 или 5,5.
Пример 46. Дана трапеция ABCD с боковыми сторонами AB 36, CD 34 и верхним основанием BC 10. Извест-
но, что cos ABC 1. Найдите BD.
3
|
B 10 |
C |
Решение. |
Про- |
|||||
|
|
|
|
ведем |
CE |
па- |
|||
36 |
|
|
|
раллельно |
AB |
||||
36 |
34 |
|
(см. рис. 50а). |
||||||
10 |
x |
|
|
Тогда |
ABCE – |
||||
|
|
параллелограмм. |
|||||||
A |
E |
D |
|||||||
AEC ABC, |
|||||||||
Рис. 50а |
|
|
DEC 180 |
||||||
|
|
|
|
||||||
AEC, |
cos DEC |
1 |
и cos DAB |
1 |
. |
||||
|
|
||||||||
|
|
3 |
|
|
3 |
||||
Обозначим ED через x. Воспользуемся теоремой косинусов для угла DEC в треугольнике DEC :
342 362 x2 2 36 x 1, 3
x2 24x 140 0.
Отсюда x 14 или x 10. Получившиеся два значения x, озна-
чают, что условию задачи соответствуют два чертежа. В одном случае CDE острый, в другом – тупой.
Воспользуемся теоремой косинусов для угла DAB в треугольнике ABD и рассмотрим два случая.
1. Пусть x 14, тогда AD 24.
05.01.2011.
BD2 362 242 2 36 24 1 1296; 3
BD 36.
В этом случае угол D – острый (см. рис. 50а), так как справедливо неравенст-
во: EC2 ED2 CD2 362 142 342
56 0.
2.Пусть x 10, тогда AD 20,
BD2 362 202 2 36 20 1 1216;
|
|
|
|
3 |
|
|
|
|
|
|
|
|
BD 8 |
|
|
. |
Пока- |
||
|
B 10 |
C |
19 |
||||||
|
|
|
жите, |
что в |
этом |
||||
|
36 |
|
случае |
угол |
D – |
||||
|
36 |
34 |
тупой |
|
(см. |
рис. |
|||
|
10 |
|
50б). |
|
|
|
|
|
|
|
|
Ответ: |
36 или |
||||||
A |
E x D |
|
|||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
8 19. |
||||
|
Рис. 50б |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
задачи с параметрами
В геометрических задачах в качестве параметра может быть линейная или угловая величина. Количество возможных решений находится в зависимости от условия задачи и области изменения параметра.
Пример 47. Дан прямоугольный треугольник АВС с прямым углом при вершине В и углом при вершине А. Точка D – середина гипотенузы. Точка C1 симметрична точке С относительно прямой BD. Найдите угол AC1B.
Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
Решение. Так как прямая BD является серединным перпендикуляром к отрезку CC1 , то DC DC1 . С другой стороны, точка D – центр окружности, описанной около прямоугольного треугольника. Поэтому DC DB DA. Отсюда следует,
что точка C1 принадлежит описанной окружности.
Построение чертежа к этой задаче зависит от того, каково значение параметра. Возможны три случая: 1) 45 ; 2) 45 90 ; 3) 0 45 .
29

Корянов А.Г., Прокофьев А.А.
1.Если 45 ,то центральный угол
BDC 2 BAC 90 . В этом случае
ось |
BD перпендикулярна гипотенузе |
|||
AC . Точка C отобразится в точку |
A, и |
|||
угол AC1B не будет определен. |
|
|||
|
|
B |
B |
C1 |
C |
D |
A |
C |
A |
|
|
|
D |
|
|
|
C1 |
|
б |
|
|
а |
|
|
|
|
Рис. 51 |
|
|
2. |
Пусть |
45 , |
тогда центральный |
|
угол BDC 2 90 (см. рис. 51а). В
этом случае точки C и C1 расположены по одну сторону от хорды AB . В прямоугольном треугольнике BCA 90 .
Вписанные углы, опирающиеся на одну и ту же дугу, равны. Поэтому
AC1B BCA 90 .
3.Пусть 45 , тогда центральный
угол BDC 90 (см. рис. 51б). В этом случае точки C и C1 расположены по разные стороны от хорды AB . Четырехугольник AC1BC вписан в окружность,
поэтому AC1B 180 BCA 180(90 ) 90 .
Ответ: 90 , если 0 45 ; 90 , если 45 90 ;
при 45 точка С1 совпадает с точкой А и угол не определен.
Пример 48. Периметр равнобедренного треугольника равен Р, одна из его сторон равна а. Найдите вторую сторону треугольника.
Решение. Если основание треугольника равно а, то боковая сторона равна
P a . Используя неравенство треуголь-
2
ника, получаем систему
|
|
P a |
|
P a |
||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
2 |
|
||||
|
|
|
|
P a |
||||
P a |
||||||||
|
|
|
|
|
|
|
a |
|
2 |
|
|
2 |
|
||||
|
|
|
|
|
|
|
||
|
P |
|
a |
|
|
2 |
||
или |
a 0
05.01.2011.
Пусть боковая сторона треугольника равна а, тогда основание равно P 2a . Запишем условия
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|||||||
P 2a a a |
|
|
|
|
|
a |
|
|
|
|
|
||||||||||
|
|
|
|
|
4 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
или |
|
P |
|||||||||||||
a P 2a a |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
P |
|
|
|
P |
|
|
|
|
|
|
|||||||
Ответ: если |
a |
, то одно реше- |
|||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
4 |
|
|
2 |
|
|
|
P a |
|
|
P a |
|
|||||||
|
|
|
|
|
|
|
ние a, |
|
, |
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
P |
|
|
|
P |
|
|
|
|
|
|
2 |
|
2 |
|
||||||
если |
a |
, то два решения a, a, |
|||||||||||||||||||
|
|
||||||||||||||||||||
4 |
|
2 |
|
|
|
|
|
|
|
P a |
|
|
P a |
|
|||||||
|
|
|
P 2a или a, |
|
, |
; |
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
P |
|
2 |
|
2 |
|
||||||
при a 0 |
или при a |
решений нет. |
|||||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
Пример 49. В параллелограмме ABCD |
|||||||||||||||||||||
известны стороны |
AB a, BC b, и |
||||||||||||||||||||
BAD . Найдите расстояние между центрами окружностей, описанных около треугольников BCD и DAB.
Решение. Диагональ BD разбивает параллелограмм на два равных треугольника BCD и DAB . Поэтому по разные стороны от прямой BD расположены центры O и O1 описанных около них окружностей, лежащие на серединном перпендикуляре OO1 к их общей стороне
BD. |
Следовательно, |
OO1 |
2OM , где |
||
точка |
M |
середина |
BD. |
Рассмотрим |
|
следующие случаи. |
|
|
|||
1. |
Если |
90 , то |
центр O лежит |
||
внутри треугольника DAB (см. рис. 52а). |
|||||
Тогда |
получаем |
|
BOD 2 , |
||
BOM |
1 |
BOD . Из треугольника |
|||
|
|||||
|
2 |
|
|
|
|
BOM |
находим OM BM ctg . Тогда |
||||
OO1 2OM 2BM ctg BD ctg .
BD находим из треугольника DAB :
BD 
 a2 b2 2abcos .
a2 b2 2abcos .
Следовательно,
OO1 
 a2 b2 2abcos ctg .
a2 b2 2abcos ctg .
2. Пусть 90 , тогда точки O и O1
совпадают и OO1 0 (см. рис. 52б).
30
