- •1. Загальні поняття про числову послідовність, функцію та їх границі
- •Поняття числової послідовності. Поняття границі числової послідовності
- •Деякі способи задання послідовності
- •Монотонні послідовності
- •Нижня та верхня межа
- •Границя послідовності
- •Геометричний зміст границі послідовності
- •Основні властивості границь послідовності :
- •Поняття функції. Поняття границі функції
- •Способи задання функції:
- •Поняття границі функції
- •Узагальнення на випадок нескінченості
- •Односторонні границі. Ліва та права границя функції
- •Теореми про границі функцій. Властивості границь
- •Деякі важливі границі
- •Границі числової послідовності і функції
- •Список використаної літератури
Поняття границі функції
Нехай функція
![]() визначена
у всіх точках проміжку
визначена
у всіх точках проміжку
![]() ,
за винятком, можливо, деякої точки
,
за винятком, можливо, деякої точки
![]() .
Побудуємо послідовність значень
аргументу функції
:
.
Побудуємо послідовність значень
аргументу функції
:
![]() ,
,
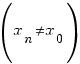 (1)
(1)
таку, щоб всі члени
послідовності належали проміжку
і
послідовність збігалась до точки
![]() :
:
![]() .
.
Тоді значення функції
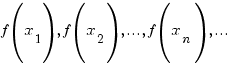 .
(2)
.
(2)
також утворять деяку числову послідовність.
Говорять, що число
![]() є
границею функції
при
є
границею функції
при
![]() ,
що прямує до
,
якщо для будь-якої послідовності значень
аргументу (1), яка збігається до числа
,
послідовність значень функції (2)
збігається до числа
,
і пишуть
,
що прямує до
,
якщо для будь-якої послідовності значень
аргументу (1), яка збігається до числа
,
послідовність значень функції (2)
збігається до числа
,
і пишуть
![]() .
.
Примітка. Це визначення границі функції називається визначенням границі по Гейне.
Існує й інше, еквівалентне тому, що вище, визначення границі функції.
Говорять, що число
є
границею функції
при
,
що прямує до
,
якщо для будь-якого додатнього числа
![]() знайдеться
таке додатне число
знайдеться
таке додатне число
![]() ,
яке залежить від
,
що при всіх
,
яке залежить від
,
що при всіх
![]() ,
які задовільняють нерівність
,
які задовільняють нерівність
![]() ,
,
виконується нерівність
![]() .
.
Примітка. Це визначення границі функції називається визначенням границі по Коші.
Узагальнення на випадок нескінченості
Сформовані вище
означення границі функції по Гейне і
по Коші можуть бути узагальнені і на
випадок, коли замість числа
береться
![]() (або
(або
![]() ).
).
Говорять, що число
є
границею функції
при
,
що прямує до
,
якщо для будь-якого додатнього числа
знайдеться
таке додатне число
![]() ,
що для всіх
,
які задовільняють нерівність
,
що для всіх
,
які задовільняють нерівність
![]() ,
виконується нерівність
,
виконується нерівність
;
в цьому випадку пишуть
![]() .
.
Говорять, що функція
прямує
до
при
прямуванні
до
,
якщо для будь-якого скільки завгодно
великого додатнього числа
![]() знайдеться
таке додатне число
знайдеться
таке додатне число
![]() ,
що для всіх
,
які задовільняють нерівність
,
що для всіх
,
які задовільняють нерівність
,
і таких, що належать області визначення функції, виконується нерівність
![]() ;
;
в цьому випадку пишуть
![]() при
при
![]() ,
або
,
або
![]() .
.
Односторонні границі. Ліва та права границя функції
Нехай функція
визначена
на проміжку
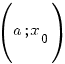 .
Число
називають
лівою
границею функції
в
точці
і
пишуть
.
Число
називають
лівою
границею функції
в
точці
і
пишуть
![]() ,
,
якщо для будь-якого
числа
![]() знайдеться
додатнє число
,
яке залежить від
,
таке, що для всіх
знайдеться
додатнє число
,
яке залежить від
,
таке, що для всіх
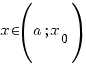 ,
які задовільняють нерівність
,
які задовільняють нерівність
![]() ,
виконується нерівність
,
виконується нерівність
.
Аналогічно визначається права границя функції . Для позначення правої границі функції в точці використовується позначення
![]()
Ліва і права границі функції називаються односторонніми границями.
Якщо функція визначена на проміжку , за винятком, можливо, точки , то для існування границі
необхідно і достатньо, щоб права і ліва границі функції в точці існували і були рівні:
![]() .
.
Теореми про границі функцій. Властивості границь
1)
Якщо функції
і
![]() мають
границі при
,
який прямує до
мають
границі при
,
який прямує до
![]() ,
то функції
,
то функції
![]() ,
,
![]() ,
,
![]() також
мають границі при
,
який прямує до
і
також
мають границі при
,
який прямує до
і
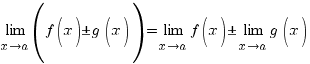
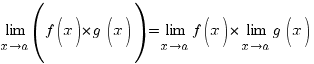
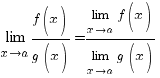
В останньому
випадку припускається, що функція
не
перетворюється в нуль в досить малому
околі точки
і
![]() .
.
2)
Якщо при
,
що прямує до
,
функція
має
границю, рівну
,
і ця границя більше числа
![]() ,
то для достятньо близьких до
значень
функція
задовільняє
нерівність
,
то для достятньо близьких до
значень
функція
задовільняє
нерівність
![]() .
.
Деякі важливі границі
В теорії границь важливе місце займають перераховані нижче границі 1)-4) за допомогою яких обчислюється багато границь від елементарних функцій:
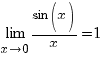
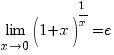
![]()