1.8.8. Таблица

Здесь сосредоточены все операции, отвечающие за вставку таблиц в документ Word. Можно вставить уже готовую таблицу, например, из Microsoft Excel, а можете просто нарисовать в документе новую, пользуясь стандартными средствами Word. Здесь же можно установить параметры сортировки строк в таблице (или текстовом фрагменте).

1.8.9. Окно

В том случае, если открыто несколько документов Word одновременно, это меню поможет переходить от одного к другому, а также управлять параметрами отображения всех открытых окон.

1.8.10. Справка «?»

Это меню отображает содержание справки; ищет тему справки по выделенным или набранным ключевым словам.

В зависимости от версии Word количество различных стандартных панелей инструментов с заданными наборами кнопок-пиктограмм колеблется от восьми (Word 6.0) до шестнадцати (Word 2000).

Набор выводимых на экран кнопок, в составе каждой из панелей, может быть изменен по желанию пользователя. Сам пользователь может создать свои панели с кнопками-пиктограммами, выбирая пиктограммы из заданного набора или создавая их самостоятельно.

Задания

1. Рассмотрим перевернутый маятник, ось которого находится на тележке, приводимой в движение мотором.

Внешняя сила U(t) изменяет положение тележки x(t) и маятника. Предполагая, что угол (t) и d(t)/dt измеримы, мы можем с помощью соответствующего управляющего устройства обеспечить такую силу u(t), что маятник без учета малых отклонений будет оставаться в вертикальном положении. Такие малые отклонения необходимы для работы управляющего устройства.

Получим уравнения состояния этой модели. Объект описывается двумя уравнениями: уравнением равновесия сил

ml"(t) + (М + т)х"(t) = u(t) (1)

и уравнением равновесия моментов сил

(J + ml²)”(t) + mlx”(t)cos (t)-mglsin(t) = 0, (2)

где, если угол  (t) мал, можно положить sin (t) =  (t) и cos(t) = l. Символ J обозначает момент инерции маятника относительно центра масс, g - ускорение силы тяжести, смысл остальных величин следует из рисунка. Для маятника длиной в 2l момент инерции J = ml²/З и уравнения (2) при малых углах (t) упрощается и принимает вид

1,33ml²”(t) + mlx”(t)-mgl(t) = 0.

Из этого уравнения следует

x”(t)= -1,33l”(t) - g(t). (3)

Подставляя (3) в (1) и вводя угловую скорость (t) = ’(t), получим уравнение состояния

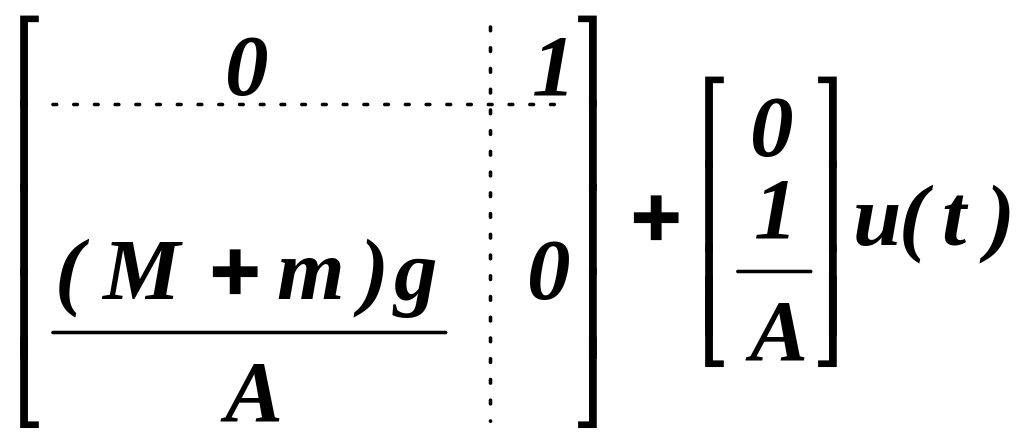= , (4)

где А = [т1-1,33(М + т)1].

Знание вектора начальных условий и силы u(t) при t > t₀ позволяет решить уравнение (4).

2. Получить уравнение состояния RI-C - цепи показанной на рисунке. Динамическое поведение этой системы полностью определяется при t > t0, если известны начальные значения i(t0) и е_с(t0) и входное напряжение e(t) при t > t0. Следовательно, эта система полностью определяется переменными состояния i(t) и е_с(t).

П еременные состояния можно, однако, выбрать по-разному. Для указанных переменных состояния i(t) и e_c(t) имеем

Li'(t) + Ri(t) + e_c(t) = e(t),

Се_с(t)' = i(t),

и ли в векторно-матричной форме, что представляет собой математическую модель заданной системы в пространстве состояний.

3. Метод Ньютона решения нелинейного скалярного уравнения. В основе метода Ньютона лежит линеаризация нелинейного уравнения. Пусть имеется нелинейное уравнение

f(x) = 0, (1)

которое будем рассматривать в S = {х: |х-х⁽⁰⁾| r}. Предположим, что производная в S. В точке х⁽⁰⁾ проведем линеаризацию (1), т.е. заменим в (1) функцию f(x) линейной функцией, проходящей через х⁽⁰⁾ и имеющей производную, равную . Получим линеаризованное уравнение

+ (х - х⁽⁰⁾) = 0 (2)

Найдем корень уравнения (2). Обозначая , имеем

(3)

Теперь произведем линеаризацию (1) в точке , повторим все этапы получения формулы (3), заменяя при этом х⁽⁰⁾ на , а на х⁽⁰⁾). Таким образом, для произвольного к получим формулу

к = 0,1,2,…, (4)

метода Ньютона приближенного определения корня уравнения f(x) = 0. Метод Ньютона называют еще методом касательных, что вполне соответствует геометрическому смыслу линеаризации на одном шаге.

4. Численное решение регуляризированных уравнений в частотной области. Решение регуляризированных уравнений удобно выполнять с помощью преобразования Фурье. Достоинством такого подхода является непосредственное определение частотой характеристики идентифицируемого объекта, простота и малое время расчетов. Действительно, для нахождения регуляризированной частотной характеристики с помощью уравнений требуются выполнение лишь арифметических операций.

и

приведена блок-схема алгоритма решения регуляризированных задач идентификации в частотной области. Исходные данные соответствующей программы являются спектральные плотности входного, входного - выходного сигналов, а также области значений w и a.

Для иллюстрации процедуры регуляризации в частотной области приведены результаты решения первой модельной задачи. Здесь обозначено: Wt(jw), Wp(jw) – точная и расчетная амплитудно-частотная характеристика (АЧХ); - точная и расчетная фазочастотная характеристика (ФЧХ).

5. Критерий Peyca-Гурвица. Рассмотрим систему линейных дифференциальных уравнений с постоянными коэффициентами

(1)

Предположим сначала, что матрица А имеет только простые собственные: значения и собственные векторы hi т.е. . Тогда общее решение уравнения (I) имеет вид: где С_i- произвольные постоянные. При наличии кратных собственных значений приведем матрицу А к жордановой форме. Если есть кратное собственное значение, то ему соответствуют т(і) клеток Жордана Bj размерности s(j), . Каждой такой клетке Жордана Bj соответствует серия векторов таких, что ,

При этом решения уравнения (I) являются функциями вида

(2)

Количество линейно независимых решений вида (2) равно n. Общее решение уравнения (1) есть линейная комбинация из частных решений вида (2).

6. Оптимальное управление намоткой привода. На рисунке изображен механизм для намотки провода.

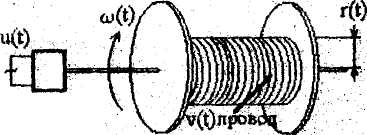
Во время намотки диаметр катушки увеличивается, что приводит к увеличению момента инерции катушки g(t). Для поддержания постоянной линейной скорости намотки v(t) = v₀ необходимо во время намотки уменьшать угловую скорость так, чтобы

. (1)

Уравнение вращения катушки имеет вид

(2)

В уравнении (2) использованы обозначения; U(t) - напряжение на входе электродвигателя; к - коэффициент пропорциональности между вращающим моментом двигателя и его входным напряжением; - коэффициент трения вращения. Управлением в данном случае является U(t), а регулируемой величиной (t), которую необходимо менять так, чтобы выполнялось условие (1).

Пусть U _ном(t) * _ном (t) - невозмущенное движение (или номинальный режим работы системы). Для возмущенных значений соответствующих переменных х(t) = g(t)[ (t) - _ном (t)] получаем уравнение

= - g^-1 (t) + ku(t), (3)

Критерий качества, подлежащий минимизации, естественно выбрать в виде

J(u) = [(r(t)g^-1 (t)x(t)² +pu² (t)]dt, p>0. (4)

Первое слагаемое в интеграле (4) пропорционально кинетической энергии вращающейся катушки, а второе - электрической энергии расходуемой электродвигателем.

7. Формула трапеций. Пусть [0,h], h>0 - рассматриваемый интервал. Предположим, что f(x) C² [0,h]. Запишем соотношение

I = в виде

,

где взяты два узла = 0, = h и соответствующие веса q_o = qi = h/2. Получаемая квадратурная формула Q = h[f(0)+f(h)]/2 называется формулой трапеций для одного шага. Название связано с тем фактом, что последнее выражение при положительных f(0) и f(h) является формулой для площади трапеции с основаниями fl(0), f(h) и высотой h. Приведем теорему об оценке погрешности R.

Теорема. Пусть f(x) C² [O, h]. Тогда погрешность квадратурной формулы трапеций R(h,f) имеет вид

R(h,f) = f’’( ),

где - некоторая точка интервала [0, h].

8. Формула Симпсона. Пусть [-h,h], h >0 (см. рис.) - рассматриваемый интервал. Предположим, f(x) C’ [-h, h]. Запишем соотношение

,

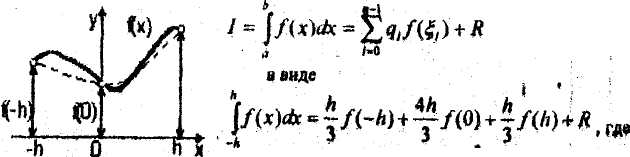где взяты три узла из (1) соответствующие веса .

Получаемая квадратурная формула называется формулой Симпсона или формулой napабол. Последнее название связывается с тем, что последнее выражение – формула интеграла от параболы, проведенной через точки (-h,f(-h)), (0,F(0)), (h,f(h)) плоскости (х, у). Покажем это. Парабола, проходящая через указанные точки, записывается в интерполяционной форме:

.

Вычисляем интеграл

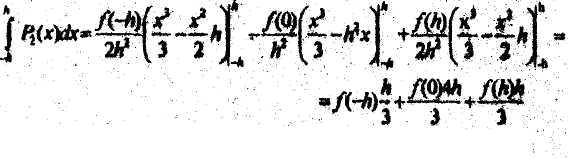
получаем правую часть квадратурной формулы парабол. Теорема об оценке погрешности R. Пусть Тогда погрешность квадратурной формулы Симпсона R(h, f) имеет вид

где - некоторая точка интервала [-h, h].