0

Л.Д. Письменко

СЕЧЕНИЕ ПОВЕРХНОСТИ

ПЛОСКОСТЬЮ.

РАЗВЕРТКИ ПОВЕРХНОСТЕЙ.

Ульяновск 2005

1

Федеральное агентство по образованию Государственное образовательное учреждение высшего

профессионального образования Ульяновский государственный технический университет

Л.Д. Письменко

СЕЧЕНИЕ ПОВЕРХНОСТИ

ПЛОСКОСТЬЮ.

РАЗВЕРТКИ ПОВЕРХНОСТЕЙ.

Методические указания и варианты заданий к расчетно-графической работе для студентов первого курса факультета информационных систем и технологий направлений 654600, 653700

Ульяновск 2005

4

ВВЕДЕНИЕ

При выполнении чертежей деталей машин нередко встречаются задачи на построение проекций сечений поверхности плоскостью. Кроме того, на чертежах приходится выполнять построение разверток поверхностей деталей. Это необходимо для раскроя листового материала, из которого изготовляются детали. К таким деталям относятся части трубопроводов, вентиляционных устройств, кожухов машин, ограждений станков и др.

Для усвоения основ проекционного черчения большое значение имеет решение задач на построение прямоугольных и аксонометрических проекций сечений поверхности плоскостью, а также построение действительного вида сечений и разверток поверхностей.

1. ПОНЯТИЕ О СЕЧЕНИЯХ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ

Сечение поверхности плоскостью представляет собой плоскую фигуру, ограниченную замкнутой линией, все точки которой принадлежат как секущей плоскости, так и поверхности.

При пересечении плоскостью многогранника (например призмы, пирамиды и т.д.) в сечении получается многоугольник с вершинами, расположенными на ребрах многогранника.

Проекциями сечения многогранников, в общем случае, являются многоугольники, вершины которых принадлежат ребрам, а стороны - граням многогранника. Поэтому задачу по определению сечения многогранника можно свести к многократному решению задачи по определению точки встречи прямой (ребер многогранника) с секущей плоскостью или к задаче по нахождению линии пересечения двух плоскостей (грани многогранника и секущей плоскости).

Первый путь решения называют способом ребер, второй – способом граней. Какому из способов следует отдать предпочтение, надо решать в каждом конкретном случае.

Первый способ предпочтителен, если некоторые ребра многогранника являются проецирующими, второй – если некоторые грани многогранника являются проецирующими плоскостями. В ряде случаев целесообразно комбинированное применение обоих способов.

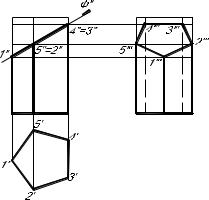
Пример построения линии пересечения поверхности пятиугольной призмы с фронтально проецирующей плоскостью Ф /Ф′′/ на рис 1.

Рис.1 Сечение призмы плоскостью

5

Фигура сечения пятигранной призмы плоскостью Ф представляет собой плоский пятиугольник 1 2 3 4 5. Для построения проекций фигуры сечения находят проекции точек пересечения плоскости Ф с ребрами призмы и соединяют их прямыми линиями.

Фронтальные проекции этих точек получаются при пересечении фронтальных проекций ребер призмы с плоскостью Ф′′ / 1′′ 2′′ 3′′ 4′′ 5′′/

Горизонтальные проекции точек пересечения 1′ 2′ 3′ 4′ 5′ совпадают с горизонтальными проекциями ребер.

Имея две проекции этих точек, по принадлежности находят профильные проекции 1′′′ 2′′′ 3′′′ 4′′′ 5′′′. Полученные точки 1′′′ 2′′′ 3′′′ 4′′′ 5′′′ соединяют прямыми линиями и получают профильную проекцию фигуры сечения.

При пересечении плоскостью поверхности вращения (цилиндра, конуса и др.) фигура сечения часто ограничена кривой линией. Точки этой кривой находят при помощи вспомогательных линий – прямых или окружностей, взятых на поверхности. Точки пересечения этих линий с секущей плоскостью будут искомыми точками контура криволинейного сечения.

Решение задачи по построению сечения поверхности вращения плоскостью значительно упрощается, если секущая плоскость занимает проецирующее положение. В этом случае одна из проекций сечения – отрезок прямой и принадлежит следу плоскости. Построение второй проекции сечения сводится к многократному решению ранее рассмотренной задачи по нахождению второй проекции точки, принадлежащей поверхности, если известна хотя бы одна ее проекция. Ниже рассматриваются задачи, связанные с построением линий пересечения сферической, цилиндрической и конической поверхностей вращения,

атакже сечений тел, представляющих собой различные комбинации из отсеков перечисленных поверхностей, проецирующими плоскостями.

Сферическая поверхность, как известно, любой плоскостью пересекается по окружности.

При пересечении цилиндрической поверхности проецирующими плоскостями могут быть получены две образующие прямые (секущая плоскость параллельна оси цилиндра), окружность (секущая плоскость перпендикулярна оси цилиндра) или эллипс (секущая плоскость пересекает все образующие цилиндра).

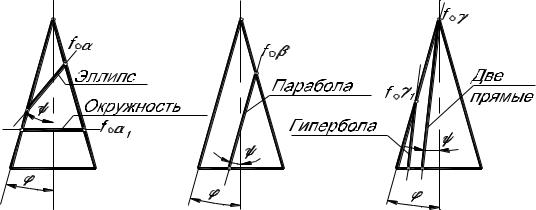
Поверхность прямого кругового конуса в своем роде уникальна, она служит носителем целого ансамбля кривых (окружности, эллипса, параболы и гиперболы),

атакже двух пересекающихся прямых (рис. 2).

Рис. 2. Конические сечения а - ψ > φ; б – ψ = φ; в – ψ < φ

7

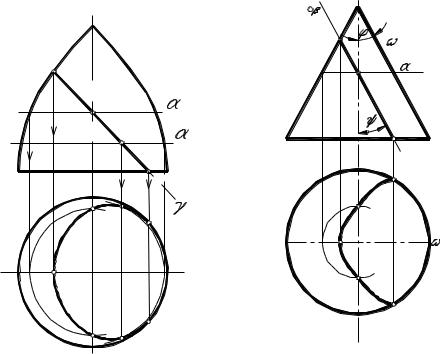
Пример 3 . Построить три проекции тела со сквозным вырезом. Определить видимость (рис. 5).

Решение. Изображенное на рисунке тело состоит из двух частей – вертикального кругового цилиндра и половины шара, из которых вырезана часть, ограниченная двумя профильными плоскостями уровня и фронтально проецирующей плоскостью. При пересечении этими плоскостями уровня цилиндрической части тела в сечениях образуются два прямоугольника и часть эллипса, а в шаровой части – два полукруга. Решение начинают с построения опорных точек A, B, C, D, E, F, K, L на поверхностях заданного тела.

Поскольку профильные плоскости уровня перпендикулярны поверхности плоскости проекций π1 , то горизонтальные проекции B′A′C′ и F′L′K′ сечений, образованных этими плоскостями, совпадают с вырожденными проекциями последних.

Горизонтальная проекция B′C′E′K′F′D′ части эллипса совпадает с очерком цилиндра на плоскости проекций π1 .

На плоскости проекций π3 профильные проекции сечений цилиндрической части тела представляют собой отрезки прямых – образующих цилиндра.

Профильная проекция эллиптической части сечения строится по принадлежности его точек боковой поверхности цилиндра. Характер построений очевиден из рис. 5.

Профильные проекции контуров сечений шаровой части тела представляют собой полуокружности радиусов О′′′A′′′ и O′′′L′′′.

Видимость определена в приведенном примере на профильной проекции тела.

F'

B'

D'

Рис. 5 Построение проекций тела с вырезом