МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГБОУ ВПО «Уральский государственный экономический университет»

Центр дистанционного образования

Контрольная работа

По дисциплине: «Теория игр»

Исполнитель: студент(ка)

Группа: ГМФ -11СВ

Ф.И.О: Суставова Татьяна Валерьевна

Екатеринбург

2013

1. Решить игру с природой

а) Решить игру с природой по критерию Гурвица, α=0,4;

I) если А – матрица выигрышей

II) если А – матрица потерь

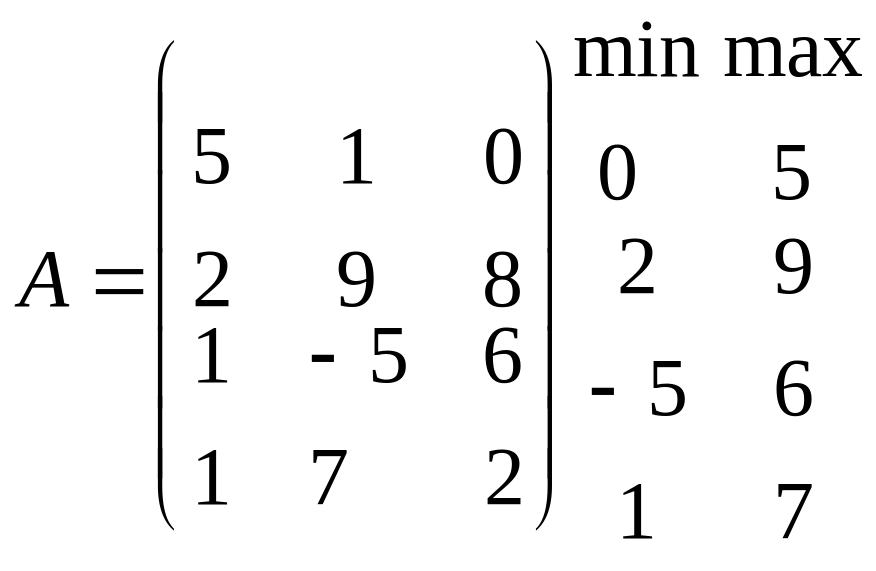
I) если А – матрица выигрышей, то оптимальной является 2 стратегия

II) если А – матрица потерь, то оптимальной является 3 стратегия

б) Решить игру с природой по критерию Лапласа;

I) если А – матрица выигрышей

II) если А – матрица потерь

I) если А – матрица выигрышей, то оптимальной является 2 (19) стратегия

II) если А – матрица потерь, то оптимальной является 3 (2) стратегия

в) Решить игру с природой по критерию Сэвиджа;

Строится матрица R – матрица риска.

Элементы находятся по формуле

I) если А – матрица выигрышей

Оптимальной является 3 (14) стратегия

II) если А – матрица потерь

Оптимальной является 1 (4) стратегия

г) Решить игру с природой по критерию Вальда.

Критерий Вальда (максиминный, минимаксный)

I) если А – матрица выигрышей, то выбирается

Оптимальной является 2 (2) стратегия

II) если А – матрица потерь, то выбирается

Оптимальной является 1 (5) стратегия.

2. Решить игру методом Брауна, выполнить 20 итераций

h	игрок А				игрок B				Приближенные значения цены
	стратегия	Накопл. выигр. В			стратегия	Накопл. выигр. A
		В1	В2	В3		A1	A2	A3	Vn1	Vn11	Vnср
1	А1	-1	3	6	В1	-1	0	6	-1	6	2,5
2	A3	5	11	9	В1	-2	0	12	2,5	6	4,25
3	A3	11	19	12	В1	-3	0	18	3,666667	6	4,833333
4	A3	17	27	15	В3	3	8	21	3,75	5,25	4,5
5	A3	23	35	18	В3	9	16	24	3,6	4,8	4,2
6	A3	29	43	21	В3	15	24	27	3,5	4,5	4
7	A3	35	51	24	В3	21	32	30	3,428571	4,571429	4
8	A2	35	55	32	В3	27	40	33	4	5	4,5
9	A2	35	59	40	В1	26	40	39	3,888889	4,444444	4,166667
10	A2	35	63	48	В1	25	40	45	3,5	4,5	4
11	A3	41	71	51	В1	24	40	51	3,727273	4,636364	4,181818
12	A3	47	79	54	В1	23	40	57	3,916667	4,75	4,333333
13	A3	53	87	57	В1	22	40	63	4,076923	4,846154	4,461538
14	A3	59	95	60	В1	21	40	69	4,214286	4,928571	4,571429
15	A3	65	103	63	В3	27	48	72	4,2	4,8	4,5
16	A3	71	111	66	В3	33	56	75	4,125	4,6875	4,40625
17	A3	77	119	69	В3	39	64	78	4,058824	4,588235	4,323529
18	A3	83	127	72	В3	45	72	81	4	4,5	4,25
19	A3	89	135	75	В3	51	80	84	3,947368	4,421053	4,184211
20	A3	95	143	78	В3	57	88	87	3,9	4,4	4,15

Игрок А использовал 1ю (A1) стратегию 1 раз, A2 = 3, A3 = 16.

Р (А1) = 1/20

Р (А2) = 3/20

Р (А3) = 4/5

Игрок B использовал 1ю (B1) стратегию 9 раз, B2 = 0, B3 = 11.

Р (В1) = 9/20

Р (В2) = 0

Р (В3) = 11/20

Ответ:

Оптимальные стратегии 1-го игрока p = (1/20, 3/20, 4/5)

2-го игрока q = (9/20, 0, 11/20).

Цена игры W = 4,15.