Свойства плотности распределения вероятностей:

1. Плотность вероятности является неотрицательной функцией:

f(x) 0, (19)

2. Вероятность того, что в результате испытания непрерывная случайная величина примет какие-либо значения из интервала (а; b), равна:

Р (а<X<b)= , (20)

3. Определенный интеграл в пределах от -∞ до +∞ от плотности вероятности непрерывной случайной величины равен единице (условие нормировки):

, (21)

4. Определенный интеграл в пределах от -∞ до x от плотности вероятности непрерывной случайной величины равен функции распределения этой величины:

, (22

Под основными числовыми характеристиками непрерывной случайной величины понимают, как и в случае дискретной случайной величины, математическое ожидание, дисперсию и среднее квадратическое отклонение.

Математическое ожидание непрерывной случайной величины:

М (Х)= = , (23)

Дисперсия непрерывной случайной величины:

D (Х) = = , (24)

Среднее квадратическое отклонение, как и для дискретной случайной величины, определяется формулой:

, (25)

7. Нормальный закон распределения

Из известных видов распределения непрерывных случайных величин наиболее часто используют нормальное распределение, которое задается законом Гаусса. К нормальному закону распределения при весьма часто встречающихся условиях приближаются другие законы. Так, если мы имеем сумму большого числа независимых величин, подчиненных каким угодно законам распределения, то при некоторых общих условиях она будет приближенно подчиняться нормальному закону. Непрерывная случайная величина называется распределенной по нормальному закону (закону Гаусса), если ее плотность вероятности имеет вид

, (26)

где μ - математическое ожидание; σ² - дисперсия; σ - среднее квадратическое отклонение этой величины.

График плотности вероятности нормального закона распределения (кривая Гаусса) приведен на рис 2.

График симметричен относительно вертикальной прямой х_max = μ, причем точке х_max = μ функция имеет максимум, равный .

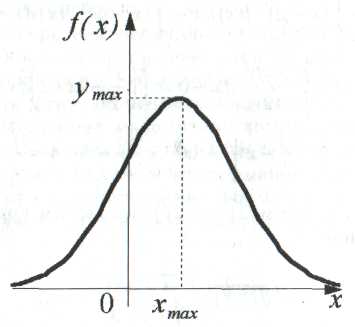
Рис.2

Подставив выражение (25) для плотности вероятности нормально распределенной случайной величины в (19), получим вероятность того, что в результате испытания нормально распределенная случайная величина примет значение из интервала (a,b):

, (27)

Введем в рассмотрение функцию

, (28)

где .

Тогда формулу (26) можно преобразовать к виду, удобному для практического применения

, (29)

Функция Ф(u) является нечетной, т.е. Ф(-u) = -Ф(u); ее значения берутся из соответствующих таблиц.

Пример 6. Предполагая, что закон распределения случайной величины X, определяемой как масса таблетки некоторого препарата, наугад выбранной из некоторой партии таблеток, является нормальным с математическим ожиданием 0,50 г и средним квадратическим отклонением 0,10 г, найти вероятность того, что масса наугад выбранной таблетки окажется в пределах от 0,55 до 0,65 г.

Решение. Полагая в формуле (21) а=0,55; b=0,65; 0,50 и 0,10 получим:

По таблице находим, что ; и для искомой вероятности получаем

.

Пользуясь (28), найдем вероятность того, что значение нормально распределенной случайной величины не выходит за пределы интервала

Это значение близко к единице. Нормально распределенная случайная величина теоретически может принимать любые значения из интервала . Но на практике ее значения обычно не выходят за пределы интервала и имеет место правило трех сигм: отклонения значений нормально распределенной случайной величины от ее математического ожидания по абсолютной величине практически не превышают ее утроенного среднего квадратического отклонения.