6. Непрерывные случайные величины
Случайная величина называется непрерывной, если множество ее возможных значений представляет собой некоторый конечный или бесконечный промежуток числовой оси.
Например, непрерывными случайными величинами являются: температура больного в фиксированное время суток, масса наугад выбранной таблетки некоторого препарата, рост наугад выбранного студента и др.
Непрерывную случайную величину нельзя задать в виде таблицы ее закона распределения, поскольку невозможно перечислить и выписать в определенной последовательности все ее значения, а также потому, что вероятность любого конкретного значения непрерывной случайной величины равна нулю.
Одним из возможных способов задания непрерывной случайной величины является использование с этой целью соответствующей функции распределения.
Функция F(x), равная вероятности того, что случайная величина Х в результате испытания примет значение, меньшее х, называется функцией распределения данной случайной величины:
F(x) =P(X<x), (14)
Свойства функции распределения:
Функция распределения удовлетворяет неравенству:
0
F(x)
1,
(15)
Функция распределения является неубывающей функцией, т.е. из х2>х1 следует F(x2) F(x1).
3. Функция распределения стремится к 0 при неограниченном убывании ее аргумента и стремится к 1 при его неограниченном возрастании.
График функции распределения в общем случае имеет вид (рис. 1).
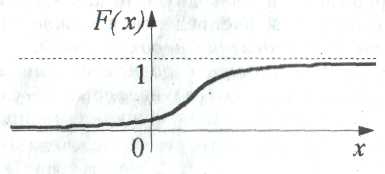
Рис.1
Из определения функции распределения вытекают два важных следствия.
Следствие 1. Вероятность того, что непрерывная случайная величина в результате испытания примет значение, принадлежащее интервалу (a,b), равна приращению функции распределения на этом интервале:
,
(16)
Следствие 2. Вероятность того, что непрерывная случайная величина в результате испытания примет определенное значение a, равна нулю:
,
(17)
Пример 5. Найти вероятность попадания в интервал (1,2) значения непрерывной случайной величины, заданной функцией распределения:
Решение. В соответствии с формулой (15) получаем:
.
Для задания непрерывной случайной величины можно также использовать плотность распределения вероятностей.
Плотностью распределения вероятностей (плотностью вероятности) f (x) непрерывной случайной величины Х называется производная функции распределения F(x) этой величины:
f(x)=F'(x), (18)