Способ вращения вокруг прямой уровня.

Этот способ на практике применяется главным образом для преобразования чертежа плоской фигуры, причем плоская фигура вращается до положения плоскости уровня. При этом плоская фигура проецируется на соответствующую плоскость проекций без искажения. Инварианты преобразования:

1. новая и старая проекция любой точки фигуры находится на одной прямой, перпендикулярной оси вращения.

2. длина новой проекции любого отрезка фигуры будет равна натуральной длине этого отрезка.

На рисунке 9.3 в плоскости, заданной треугольником АВС, проведена горизонталь через вершину А и точку 1. Горизонталь принята за ось вращения. Точки А и 1 при вращении останутся неподвижными. Точки В и С вращаются по о кружностям, которые проецируются на горизонтальной проекции отрезками прямых, перпендикулярными проекции оси. Так как треугольник должен занять горизонтальное положение, радиус вращения вершины В, например, должен проецироваться в натуральную величину. Длину радиуса R_В можно определить способом прямоугольного треугольника. Определив горизонтальное положение радиуса вращения вершины В, построим вершину С' в пересечении прямой В´1 с проекцией ее траектории вращения. Полученная проекция АВ´С´ и определяет истинную величину треугольника.

Способ замены плоскостей проекций.

С

а

ущность способа замены плоскостей проекций заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей проекций новой системой взаимно перпендикулярных плоскостей проекций (рисунок 9.4). При переходе к новой системе одну из плоскостей проекций заменяют новой плоскостью так, чтобы данный геометрический элемент занял частное положение. Инварианты преобразования: при замене плоскостей проекций расстояние от новой проекции точки до новой оси равно расстоянию от заменяемой проекции точки до старой оси проекций.

Требуется определить натуральную величину отрезка прямой АВ. Для этого нужно преобразовать прямую АВ в прямую уровня. На рисунке 9.4 а,б ось проведена параллельно горизонтальной проекции А₂В₂ прямой АВ, а новая плоскость П₄ расположена параллельно прямой АВ, которая проецируется на эту плоскость в истинную величину. Новая ось х₂₄ и плоскость проекций П₄ могут быть расположены на любом расстоянии от прямой, они могут совпадать с прямой и ее проекцией.

Основная литература: 1 осн.[65-95 ], 2 осн. [94-110 ]

Дополнительная литература: 1 доп.[29-37].

Контрольные вопросы:

1. В чем сущность преобразования проекций способом замены плоскостей проекций?

2. Назовите задачи, для решения которых достаточно заменить только одну плоскость проекций.

3. Назовите задачи, которые решаются заменой двух плоскостей проекций.

4. В чем сущность преобразования способом вращения вокруг оси, перпендикулярной плоскости проекций?

5. Укажите последовательность графических построений при определении натуральной величины плоской фигуры способом замены плоскостей проекций.

Лекция 10. Кривые линии и поверхности.

Кривая (линия) – это однопараметрическое множество точек. Кривые линия в начертательной геометрии рассматривается как траектория, непрерывно движущейся в пространстве точки, а также как линия пересечения поверхностей.

Т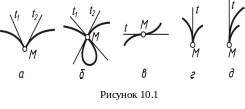 ипы линий – плоские, все точки которой принадлежат одной плоскости – (окружность, эллипс, парабола, гипербола), пространственные –все точки не принадлежат одной плоскости - винтовые (цилиндрические, конические и т.д.). Кривая может быть описана аналитически, т.е. уравнением (алгебраическим или трансцендентным), например, эллипс, парабола, гипербола и др. Если образование кривой не имеет строгой закономерности, то она задается графически, например горизонтали на плане местности.

Степень уравнения, которое выражает алгебраическую кривую, определяет порядок кривой. Геометрически порядок плоской кривой определяется числом точек ее пересечения прямой линией (как действительных, так и мнимых точек). Порядок пространственной кривой определяется числом точек пересечения кривой с плоскостью.

Свойства проекций кривой: 1) в общем случае проекции кривой линии является также кривыми линиями; 2) если точка принадлежит кривой линии, то ее проекции принадлежат одноименным проекциям этой кривой; 3) касательная к кривой линии проецируется в касательную к проекции этой кривой, если направление не параллельно касательной. Точка кривой называется обыкновенной, если в этой точке можно построить единственную касательную к кривой. Точка называется особой, если в ней не определено положение касательной. К ним относятся (рисунок 10.1): а) угловая точка, в которой кривая имеет две касательные и направление ее изменяется «скачком»; б) узловая точка, в которой кривая пересекает себя; в) точка перегиба, в которой изменяется направление движения касательной; г) точки возврата первого рода; д) точка возврата второго рода.

О бразование и задание поверхности. В начертательной геометрии поверхность рассматривается как непрерывное множество последовательных положений линии, перемещающейся в пространстве по определенному закону. Такой способ образования поверхностей называется кинематическим. Линию l, которая при своем движении образует поверхность, называют образующей (рисунок 10.2). Образующая может перемещаться по какой-либо другой неподвижной линии m, называемой направляющей. Совокупность геометрических элементов и условий, необходимых и достаточных для однозначного задания поверхности называют определителем. Определитель поверхности содержит две части – геометрическую и алгоритмическую.

Поверхность считается заданной, если относительно любой точки пространства можно решить вопрос о ее принадлежности данной поверхности.

Поверхностью вращения называется поверхность, образованная вращением линии – образующей вокруг неподвижной прямой – оси вращения.

На проекционном чертеже ось вращения располагают перпендикулярно плоскости проекций. Окружности, по которым перемещаются все точки образующей называются параллелями. Наибольшую параллель называют экватором, наименьшую – горловиной. Если ось вращения вертикальна, то все параллели проецируются на горизонтальной проекции без искажения. Плоскости, проходящие через ось вращения, пересекают поверхность по линиям, называемым меридианами. Меридиан, расположенный в плоскости, параллельной плоскости проекц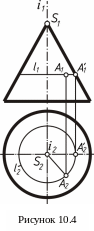 ий, называется главным и проецируется на эту плоскость проекций очерком поверхности.

На рисунке 10.4 показано как определять недостающую проекцию точки А, если задана ее только одна проекция на поверхности вращения.

При вращении прямой l вокруг оси i образуется линейчатая поверхность вращения второго порядка:

если l Ç i - коническая поверхность вращения;

если l ÷÷ i - цилиндрическая поверхность вращения;

е сли l i - однополостный гиперболоид вращения.

Вид поверхности вращения зависит от формы образующей и ее положения относительно оси вращения. При вращении кривой n-го порядка, имеющей плоскость симметрии, вокруг оси, лежащей в этой плоскости, образуется поверхность вращения n-го порядка.

1. Сфера. Образуется вращением окружности вокруг диаметра.

2. Эллипсоид вращения. Меридианом является эллипс. Если эллипс вращается вокруг большой оси, эллипсоид называется вытянутым, если вращение происходит вокруг малой оси, эллипсоид называют сжатым.

3. Параболоид вращения. Меридианом является парабола.

4 . Гиперболоид вращения. Меридианом поверхности является гипербола. Если ось вращения совпадает с действительной осью гиперболы, образуется двуполостный гиперболоид, если осью вращения является мнимая ось, то – однополостный.

5. При вращении алгебраической кривой n-го порядка вокруг произвольной прямой образуется поверхность вращения порядка 2n. Например, тор. Поверхность тора образуется вращением окружности вокруг оси, не проходящей через ее центр, но расположенной в плоскости окружности.

Поверхность, образованная движением прямой линии по заданному закону, называется линейчатой. Развертываемые линейчатые поверхности – конические и цилиндрические, торсовые. Линейчатая поверхность, образованная множеством касательных пространственной кривой, называется торсовой или поверхностью с ребром возврата.

Неразвертываемые – поверхности с плоскостью параллелизма (поверхности Каталана): цилиндроид, коноид, косая плоскость (гиперболический параболоид) (рисунок 10.5).

П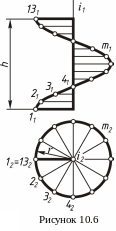 оверхность, образованная винтовым движением некоторой линии, называется винтовой поверхностью. Если при своем движении образующая пересекает ось винтового движения, то поверхность называется закрытой, в противном случае – открытой. Если образующей является прямая, то поверхность назвается геликоидом. Геликоид называется прямым, если образующая перпендикулярна оси винтового движения, в противном случае – наклонным. На рисунке 10.6 показан закрытый прямой геликоид. Если образующие открытого геликоида являются касательными некоторой цилиндрической винтовой линии, то геликоид называется винтовым торсом или эвольвентным, так как его нормальное (перпендикулярное оси) сечение представляет эвольвенту окружности.

Поверхность, образованная параллельным перемещением образующей l по направляющей m, называется поверхностью параллельного переноса.

Основная литература: 1 осн.[117-162 ], 2 осн. [67-93 ]

Дополнительная литература: 1 доп.[57-84].

Контрольные вопросы:

1. Какие кривые линии называются алгебраическими и какие - трансцендентными?

2. Какие точки кривой относят к особым?

3. Что называется определителем поверхности?

4. Укажите основные свойства поверхностей вращения?

5. Какие винтовые поверхности называют геликоидами?

6. Как построить точку и линию, принадлежащие поверхности?

7. Назовите поверхности вращения с прямолинейной образующей.

Лекция 11. Пересечение поверхности плоскостью и прямой.

Прежде чем перейти к построению линии пересечения поверхностей вращения плоскостью, рассмотрим условия получения так называемых конических сечений – кривых линий, полученных в результате пересечения конуса секущей плоскостью.

Плоскость, проходящая через вершину, пересекает конус по двум прямым – образующим конуса.

Плоскость, перпендикулярная оси, пересекает конус по окружности.

Если плоскость пересекает все образующие конуса и не перпендикулярна его оси, то сечением будет эллипс (рисунок 11.1а).

Если плоскость пересекает одну полу конуса и параллельна одной образующей конуса, то сечением будет парабола (рисунок 11.1б).

Е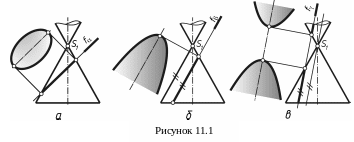 сли плоскость пересекает обе полы конуса и параллельна двум его образующим, то в сечении получится кривая, состоящая из двух симметричных ветвей – гипербола (рисунок 11.1в).

Р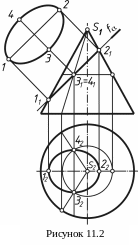 ассмотрим примеры построения линии пересечения поверхностей вращения плоскостью.

Пример 1. Построить пересечение конуса фронтально проецирующей плоскостью. Секущая плоскость является проецирующей, поэтому фронтальная проекция линии сечения совмещена с проецирующим следом плоскости f_. Полученный в сечении эллипс проецируется на плоскость П₁ отрезком 1₁-2₁, который является большой осью эллипса. Горизонтальная проекция строится с помощью линий связи. Малая ось 3-4 перпендикулярна большой оси и делит ее пополам. Точки 3 и 4 строим с помощью параллели или двух образующих конуса: S-3 и S-4. На рисунке 11.2 также построен натуральный вид сечения конуса способом замены плоскостей проекций. Дополнительные промежуточные точки могут быть построены аналогично построению точек 3 и 4.

Пример 2. Построить линию пересечения конуса плоскостью общего положения. В отличие от первого примера здесь необходимо построить обе проекции линии сечения. Точки пересечения отдельных образующих конуса с заданной плоскостью определяется с помощью вспомогательной секущей плоскости аналогично построению точки пересечения прямой с плоскостью. Сечение конуса неполное, если оно включает линию пересечения основания конуса. Две точки 1 и 2 определяются на плане в пересечении горизонтального следа h_ плоскости с окружностью основания. Точка видимости 3 определяется с помощью вспомогательной фронтальной плоскости  , проведенной через ось конуса и пересекающей плоскость по фронтали f. В пересечении ее фронтальной проекции с очерковой образующей конуса определяем проекции точки 3.

В ысшая точка линии сечения 4 расположена на линии наибольшего ската плоскости, проходящей через ось конуса. Она определяется с помощью вспомогательной горизонтально проецирующей плоскости g. Промежуточные точки линии пересечения 5 и 6 построены с помощью горизонтальной плоскости d, которая пересекает конус по окружности, а плоскость a - по горизонтали.

Основная литература: 1 осн.[117-162 ], 2 осн. [67-93 ]

Дополнительная литература: 1 доп.[57-84].

Контрольные вопросы:

1. Укажите общую схему определения точек линии пересечения поверхности проецирующими плоскостями.

2. Укажите общую схему определения точек линии пересечения плоскость общего положения.

3. Какие точки линии пересечения поверхности плоскостью называют опорными?

4. Укажите условия, при которых в сечении конуса вращения плоскостью получаются окружность, эллипс, гипербола, парабола, пересекающиеся прямые, точка.

5. Как построить высшую и низшую точки конического сечения?

Лекция 12. Взаимное пересечение поверхностей.

Для построения линии пересечения чаще всего используется способ вспомогательных поверхностей. Алгоритм решения задачи способом вспомогательных поверхностей может быть описан в общем виде следующим образом. Линией пересечения может быть прямая, плоская и пространственная кривая или любое сочетание из этих линий.

П остроим одну из точек линии пересечения поверхностей F и W. Для этого проведем поверхность S, которая пересекается F по кривой а, а с W - по кривой b. Точка А пересечения кривых а и b принадлежит обеим заданным поверхностям, следовательно, и линии их пересечения с. Аналогично, может быть найдено любое число точек линии пересечения.

Чтобы построить линию пересечения двух поверхностей, следует рассечь их рядом вспомогательных поверхностей, построив линии пересечения поверхностей данных и вспомогательных, нужно отметить общие для них точки, эти точки должны быть последовательно соединены между собой.

Точки линии пересечения двух поверхностей делятся на опорные и промежуточные. К опорным точкам относятся:

1. самая близкая и самая удаленная точка линии пересечения относительно той или иной плоскости проекций;

2. точки видимости, имеющие проекции на линии очертания;

3. точки наибольшей ширины линии пересечения и т.д.

Построение линии пересечения поверхностей следует начинать с определения ее опорных точек.

В качестве вспомогательных поверхностей чаще всего следует брать плоскости, либо сферы. Поэтому, из общего способа выделяют два, которые называются способом вспомогательных плоскостей и способом сфер.

Способ вспомогательных плоскостей. В качестве вспомогательных плоскостей могут быть приняты:

1. плоскости уровня;

2. проецирующие плоскости;

3. плоскости общего положения.

Пример. Построить пересечение трехгранной призмы с конусом вращения (рисунок 12.2). Три боковые грани призмы являются фронтально проецирующими плоскостями. Линия пересечения данных поверхностей представляет собой ломаную линию, состоящую из трех плоских кривых. Грани призмы пересекают поверхность конуса по окружности, неполному эллипсу и неполной параболе.