2.2.4. Счётчики с использованием единичного триггера
Эти счётчики построены на JKRS-триггерах и могут иметь произвольный модуль счёта. Рассмотрим пример синтеза синхронного счётчика с модулем счёта N=3.
Синтез синхронного счётчика с произвольным порядком счёта состоит из следующих этапов:
1. Определение числа триггеров в счётчике.
2. Составление прикладной таблицы функционирования.
3. Составление карт Карно для переходов каждого триггера.
4. Запись обобщённой таблицы переходов JK-триггера.
5. Составление карт Карно и определение логических функций для каждого входа каждого триггера.
6. Составление принципиальной схемы счётчика.
1. Определение числа триггеров в счётчике по формуле: n = Int(log2N), где n -число триггеров; Int-ближайшее большее целое число; N-наибольшее число, генерируемое счётчиком; log2N-двоичный логарифм N. Для выбранного примера n = Int(log22) = 2.
2. Составление прикладной таблицы функционирования счётчика (табл. 16). Q2n , Q1n - старые состояния счётчика, Q2n+1, Q1n+1 – новые состояния счётчика.
Таблица 16
n |
Q2n |
Q1n |
Q2n+1 |
Q1n+1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
2 |
1 |
0 |
0 |
0 |
3. Составление карт Карно для переходов каждого триггера.
1 триггер 2 триггер
Q2n \Q1n |
0 |
1 |
|
Q2n \Q1n |
0 |
1 |
0 |
01 |
10 |
0 |
00 |
01 |
|
1 |
00 |
Ф |
1 |
10 |
Ф |
4. Запись обобщённой таблицы переходов JK-триггера.
Qn |
Qn+1 |
Jn |
Kn |
0 |
0 |
0 |
Ф |
0 |
1 |
1 |
Ф |
1 |
0 |
Ф |
1 |
1 |
1 |
Ф |
0 |
5. Составление карт Карно для каждого входа каждого триггера и определение логических функций для входов.
1 триггер
J1n =
K1n=1
Q2n \Q1n |
0 |
1 |
|
Q2n \Q1n |
0 |
1 |
0 |
1 |
Ф |
0 |
Ф |
1 |
|
1 |
0 |
Ф |
1 |
Ф |
Ф |
2 триггер J2n = Q1n K2n =1
Q2n \Q1n |
0 |
1 |
|
Q2n \Q1n |
0 |
1 |
0 |
0 |
1 |
0 |
Ф |
Ф |
|
1 |
Ф |
Ф |
1 |
1 |
Ф |
Составление принципиальной схемы счётчика .
Схема моделирования счётчика по модулю N = 3 в программе Electronics Workbench приведена на рис. 2.27. Первый триггер в этой схеме является счётчиком-предшественником с модулем счёта N = 2. Второй триггер увеличивает модуль счёта на единицу и поэтому называется единичным триггером.
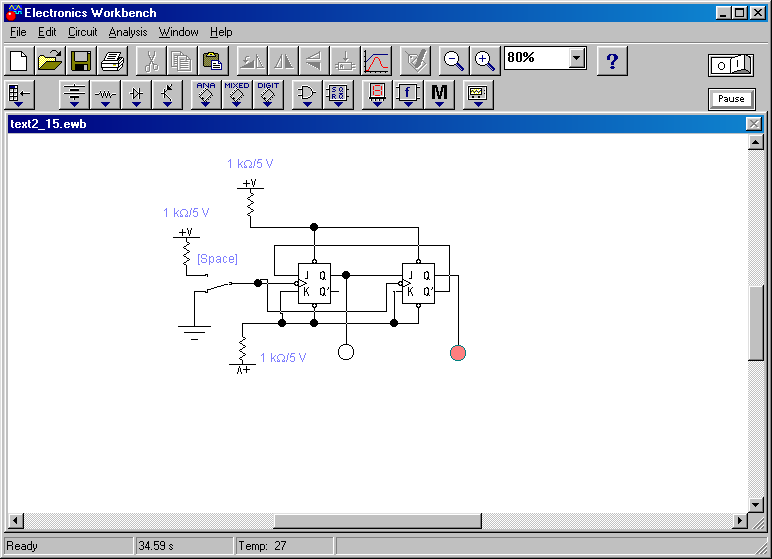
Рис. 2.27.
Анализ составленной схемы показывает, что для построения счётчика с произвольным модулем счёта необходимо выполнить следующие действия:
1) представить модуль счёта в виде совокупности чисел 2 и 1. Например: N = 3 = 2 + 1; или N = 9 = 2*2*2+1 = (2+1)*(2+1); или N = 5 = 2*2 + 1. При этом знак умножения следует трактовать как асинхронную связь между разрядами счётчика, а знак суммирования – как использование единичного триггера;
2) соединить синхронный вход единичного триггера с синхронным входом первого разряда счётчика-предшественника (счётчика модуль которого увеличивается на единицу); 3) соединить инверсный выход единичного триггера с входом J первого разряда счётчика-предшественника; 4) соединить выходы каждого асинхронного разряда счётчика-предшественника с входами J единичного триггера. Если вход J не имеет конъюнктора, то необходимо подключить внешний конъюнктор.
Пример: построить и протестировать счётчик по модулю N = 7.
Представим число 7 в виде совокупности чисел 2 и 1.
7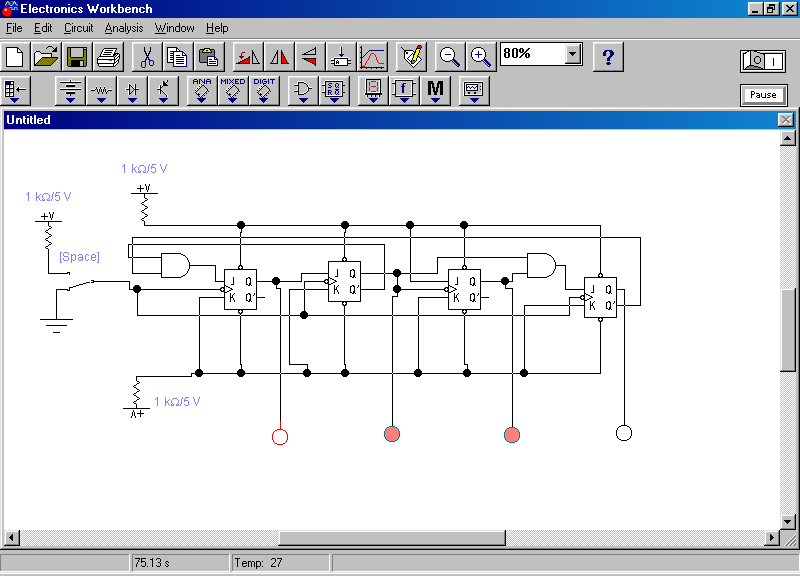
= 6+ 1 = 3*2 +1 = (2 + 1)*2 + 1. Счётчик-предшественник
имеет модуль счёта 6 и содержит два
асинхронных разряда с модулями счёта
3 и 2. В программе Electronics
Workbench при использовании
JKRS-триггеров без встроенных
конъюнкторов по JK- входам
схема счётчика имеет вид (рис.2.28).
Рис. 2.28.
В схеме присутствуют два единичных триггера: первый из них (второй слева) увеличивает на единицу модуль счёта равный двум, а второй (четвёртый слева) увеличивает на единицу модуль счёта равный 6. Счётчик работает в смешанной троично-двоичной системе. На приведенной выше схеме он содержит число 5: одна тройка и одна двойка. Состояние 6 показано ниже (рис. 2.29): две тройки.
Рис. 2.29.
Таблица
состояний счётчика, в которой нумерация
триггеров выполнена слева направо, (
-
в схеме крайний слева триггер,
соответствующий младшему разряду
счётчика) приведена ниже (табл. 17).
Таблица 17
N |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
1 |
0 |
3 |
0 |
1 |
0 |
0 |
4 |
0 |
1 |
0 |
1 |
5 |
0 |
1 |
1 |
0 |
6 |
1 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
Для моделирования этого же счётчика в программе СФЛМ используем уже принятую выше маркировку выходов триггеров и входов схемы, добавив маркировку прямого и инверсного выходов четвёртого триггера числами 16 и 17. Программа моделирования счётчика с модулём счёта N =7 и построенная с её помощью временная диаграмма (рис. 2.30) приведены ниже.
Рис. 2.30.