
- •Вопросы и упражнения
- •Семинар 2 Кинематика вращательного движения
- •Вопросы и упражнения
- •Семинар 3 Движение тел под действием силы тяжести
- •Вопросы и упражнения
- •Задачи Свободное падение. Движение тела, брошенного вертикально вверх
- •Движение тела, брошенного горизонтально
- •Движение тела, брошенного под углом к горизонту
- •Семинар 4 Динамика материальной точки и тела, движущихся поступательно
- •Вопросы и упражнения
- •Семинар 5 Силы в механике
- •Вопросы и упражнения
- •Семинар 7 работа. Мощность. Энергия. Закон сохранения энергии
- •Вопросы и упражнения
- •Семинар 8 Моменты инерции твердых тел
- •Вопросы и упражнения
- •Семинар 9 динамика вращательного движения твердого тела относительно неподвижной оси
- •Вопросы и упражнения
- •Семинар 10 законы сохранения. Закон сохранения момента импульса
- •Вопросы и упражнения
- •Семинар 11 Кинематика колебаний
- •Вопросы и упражнения
- •Семинар 12 Математический , пружинный и физический маятник
- •Задания и упражнения
- •Физический маятник
- •Семинар 14 Сложение колебаний
- •Вопросы и упражнения
- •Семинар 14 элементы механики жидкости
- •Вопросы и упражнения
- •З адачи
- •Семинар 15 Основы теории относительности
Семинар 11 Кинематика колебаний
Основные формулы
Кинематические характеристики колебательного движения:
Уравнение
гармонических колебаний (путь, смещение)
![]() ,
где
,
где
-
смещение колеблющейся точки от положения
равновесия;
![]() -
амплитуда колебаний ( максимальное
отклонение от положения равновесия);
-угловая
частота;
-
начальная фаза колебаний;
-
амплитуда колебаний ( максимальное
отклонение от положения равновесия);
-угловая
частота;
-
начальная фаза колебаний;
![]() -
фаза колебаний в момент времени
.
-
фаза колебаний в момент времени
.
Скорость точки,
совершающей гармонические колебания
![]()
Ускорение при
гармонических колебаниях
![]()
Угловая частота
колебаний
![]() ,
где
,
где
![]() и
и
![]() -
частота и период колебаний
-
частота и период колебаний
Динамические характеристики колебательного движения:
Сила-
![]()
Кинетическая
энергия
![]()
Потенциальная
энергия
![]()
Полная энергия
![]()
Вопросы и упражнения
Зависимость от времени координаты некоторой системы с одной степенью свободы имеет вид
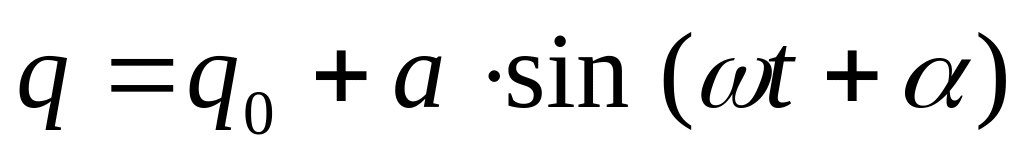 .
Какое движение совершает эта система?
Перечислите его основные параметры.
.
Какое движение совершает эта система?
Перечислите его основные параметры.Зависимость от времени координаты некоторой системы с одной степенью свободы имеет вид: 1)
 ;
2)
;
2)
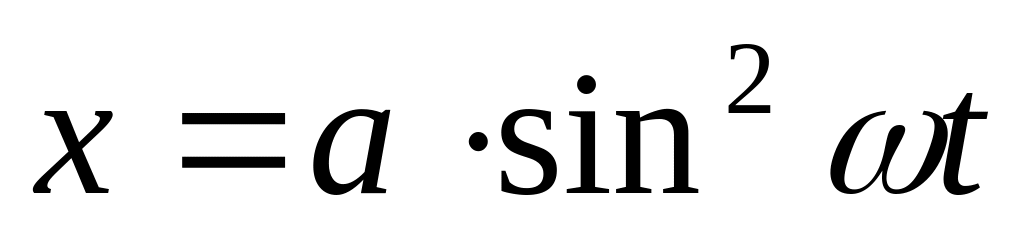 ; 3)
; 3)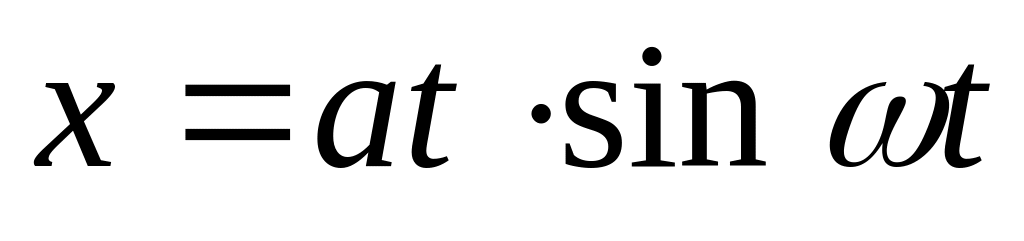 ;
4)
;
4)
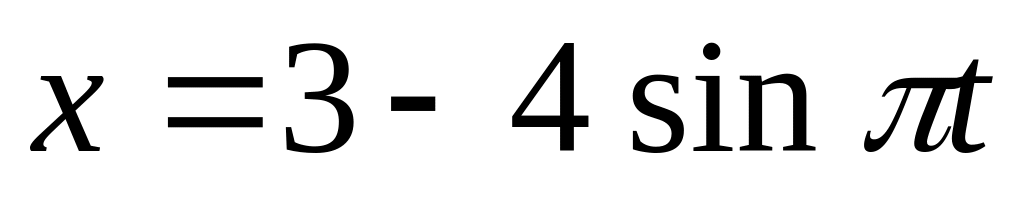 ,
Какие из зависимостей описывают
гармонические колебания? Определите
для этих случаев значения
,
соответствующих положению равновесия,
амплитуду, частоту и начальную фазу
колебаний.
,
Какие из зависимостей описывают
гармонические колебания? Определите
для этих случаев значения
,
соответствующих положению равновесия,
амплитуду, частоту и начальную фазу
колебаний.Уравнение колебаний задано в виде
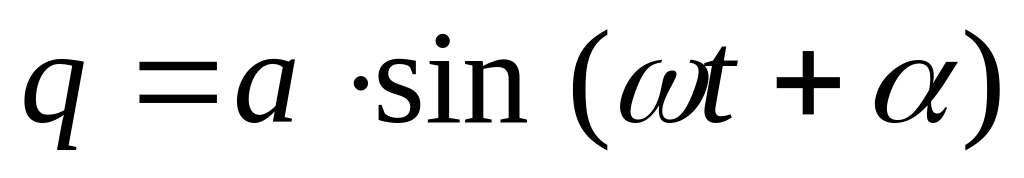 .
Чему равны: а) сила, действующая на
частицу при прохождении положения
равновесия; б) ее скорость в тот момент,
когда она находится в «крайнем»
положении.
.
Чему равны: а) сила, действующая на
частицу при прохождении положения
равновесия; б) ее скорость в тот момент,
когда она находится в «крайнем»
положении.Энергия одномерного гармонического осциллятора имеет вид
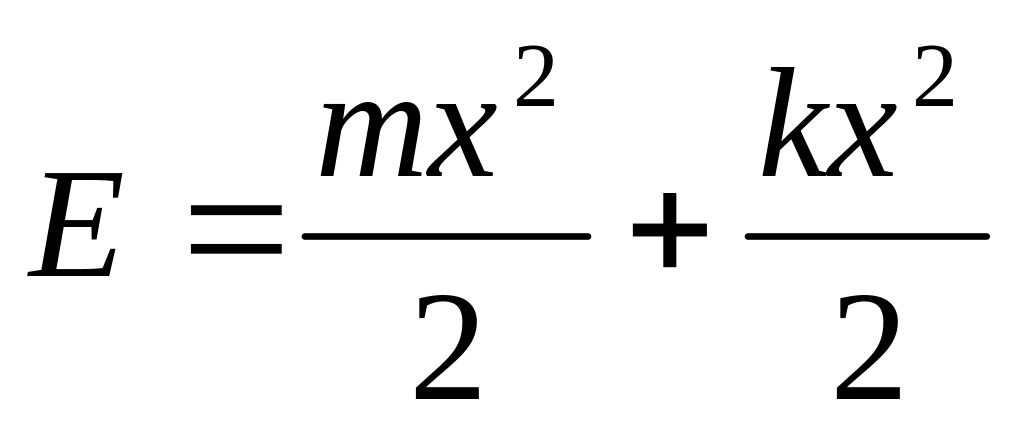 ,
где
-
масса,
-
коэффициент упругости. Найти амплитуду
колебаний и амплитуду скорости.
,
где
-
масса,
-
коэффициент упругости. Найти амплитуду
колебаний и амплитуду скорости.Частица массы совершает гармонические колебания вдоль оси около точки
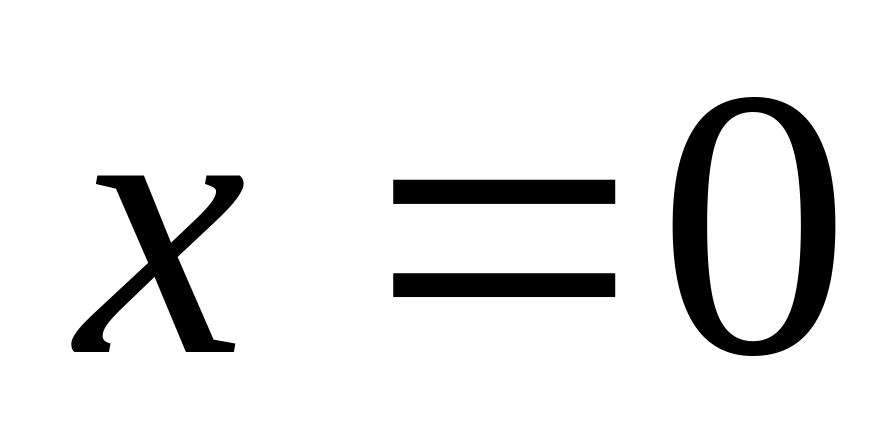 с частотой
.
В начальный момент времени
с частотой
.
В начальный момент времени
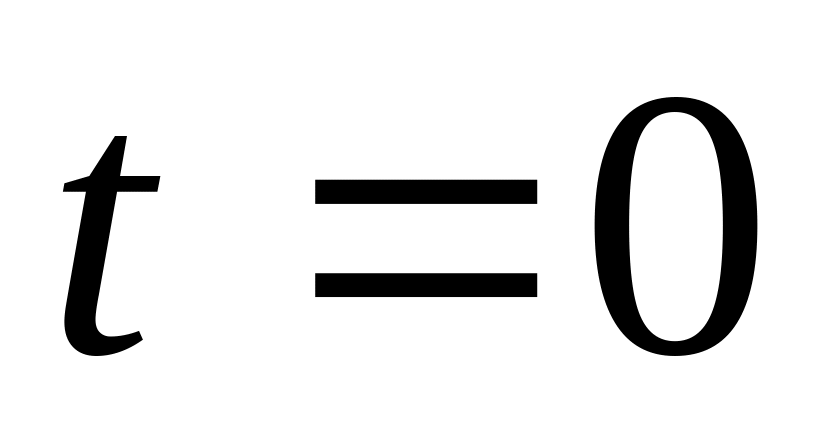 ее координата и скорость соответственно
равны: а)
ее координата и скорость соответственно
равны: а)
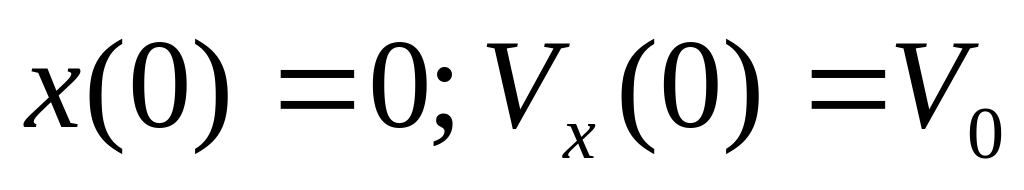 ;
б)
;
б)
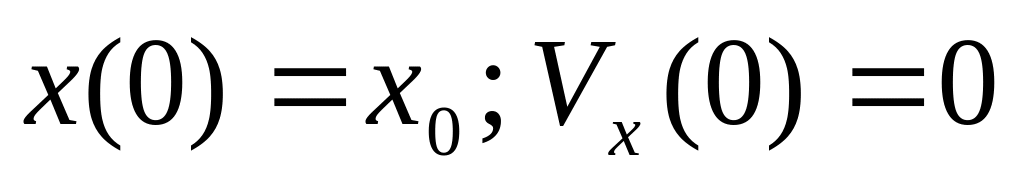 ;
в)
;
в)
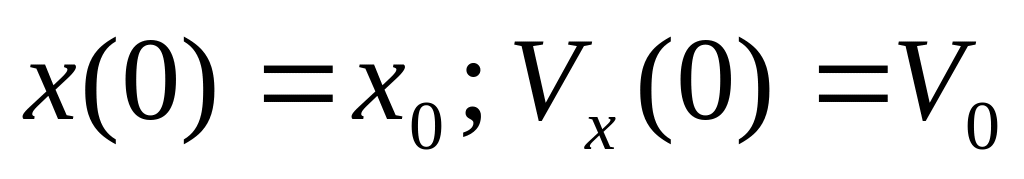 .
Определите для этих трех случаев полную
механическую энергию частицы, амплитуду
колебаний и амплитуду скорости. Написать
зависимости
.
Определите для этих трех случаев полную
механическую энергию частицы, амплитуду
колебаний и амплитуду скорости. Написать
зависимости
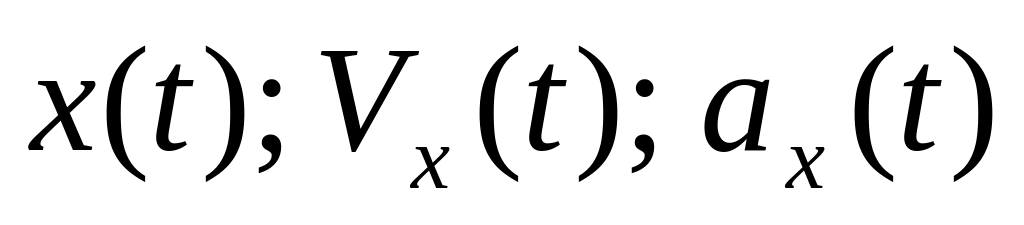 .
.Если
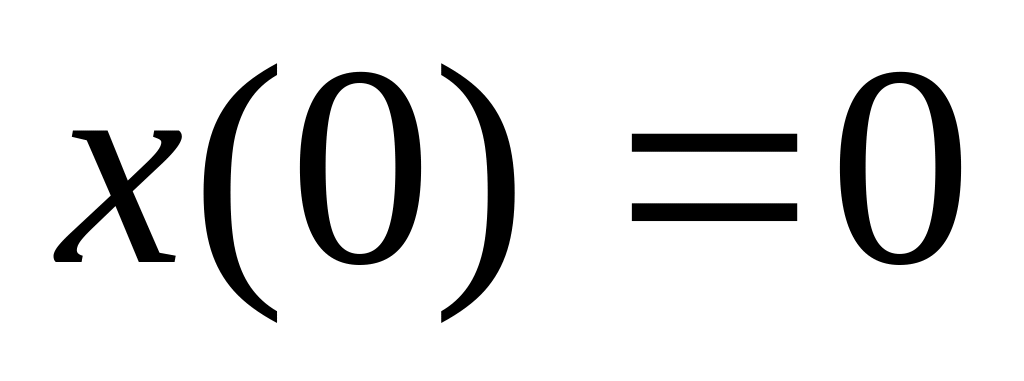 ,
а
,
а
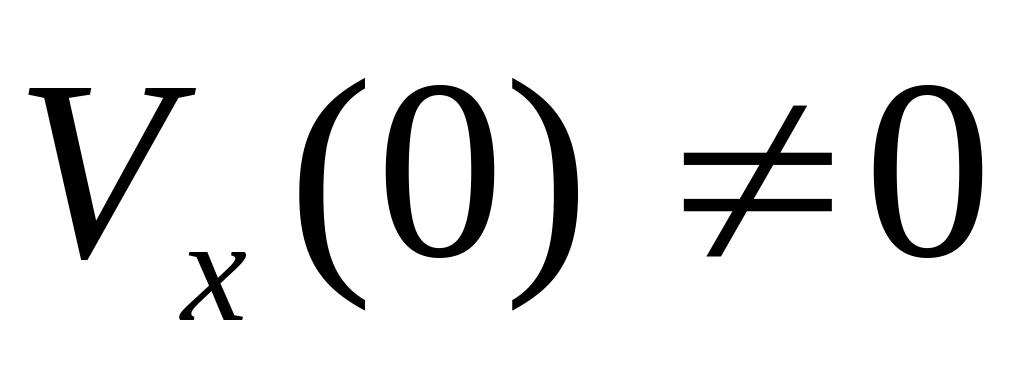 То
какая функция удобнее для записи
зависимости координаты от времени :
синус или косинус?
То
какая функция удобнее для записи
зависимости координаты от времени :
синус или косинус?для случаев а и б из задачи 5 написать зависимость от времени кинетической и потенциальной энергии частицы и изобразить полученные зависимости графически.
ЗАДАЧИ
Уравнение колебаний точки имеет вид
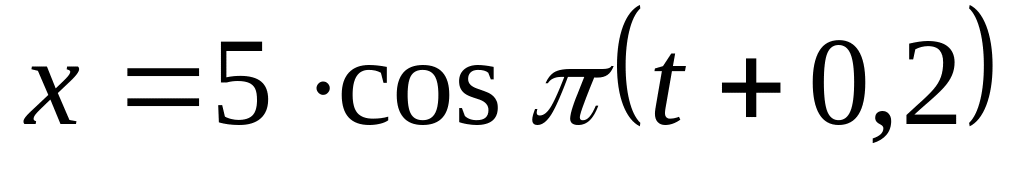 .
Определить период колебаний и начальную
фазу колебаний.
.
Определить период колебаний и начальную
фазу колебаний.Написать уравнение гармонического колебания, если начальная фаза равна
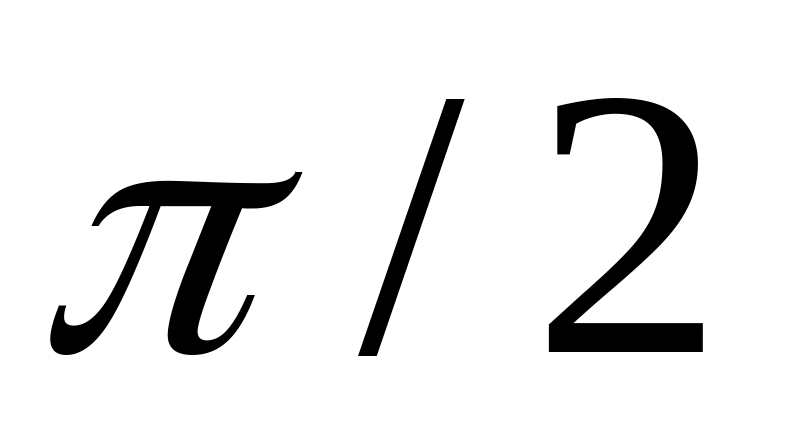 ,
амплитуда колебаний равна 5 см, а период
колебаний равен 8 с.
,
амплитуда колебаний равна 5 см, а период
колебаний равен 8 с.Некоторая точка движется вдоль оси х по закону
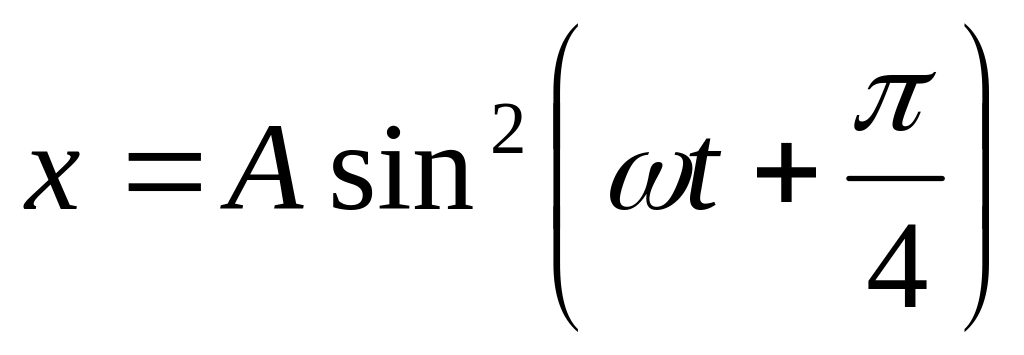 .
Найти амплитуду, период колебаний,
максимальное значение проекции скорости.
.
Найти амплитуду, период колебаний,
максимальное значение проекции скорости.Точка совершает колебания вдоль оси х по закону
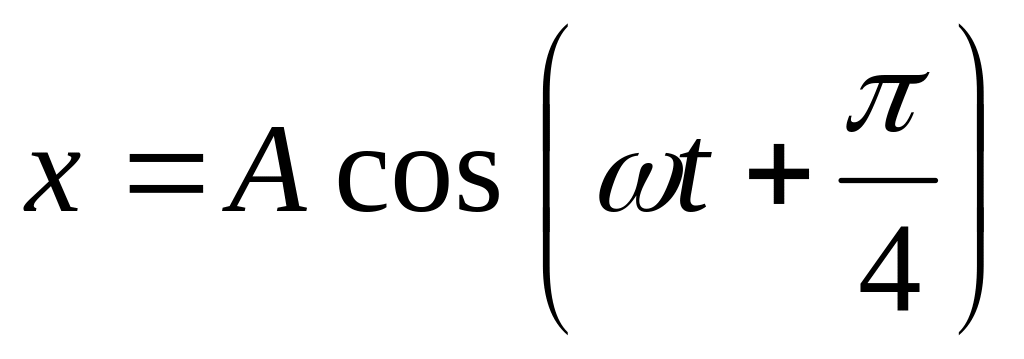 .
Построить примерные графики смещения,
проекции скорости и проекции ускорения
как функции времени.
.
Построить примерные графики смещения,
проекции скорости и проекции ускорения
как функции времени.Некоторая точка движется вдоль оси х по закону . Найти амплитуду, период колебаний, максимальное значение проекции скорости.
Начальная фаза гармонического колебания равна нулю. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?
Уравнение колебаний точки массой 1,6 г имеет вид
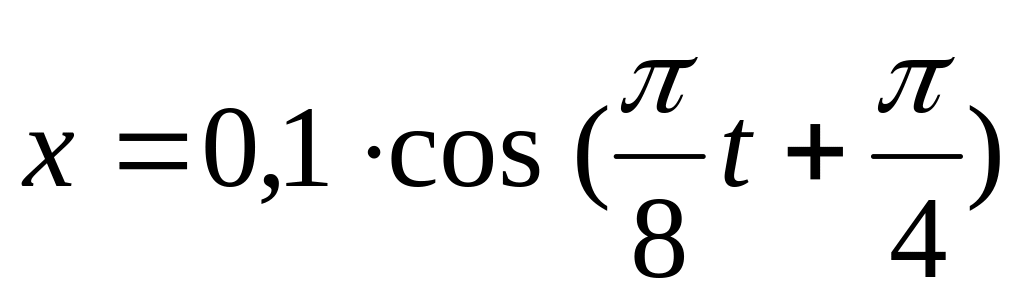 .
Построить график зависимости силы,
действующей на точку, в пределах одного
периода.
.
Построить график зависимости силы,
действующей на точку, в пределах одного
периода.Н
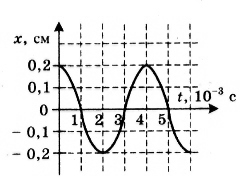 а
рисунке представлена зависимость
координаты центра шара, подвешенного
на пружине, от времени. Определить
амплитуду, период и частоту колебаний.
Записать уравнение колебаний
а
рисунке представлена зависимость
координаты центра шара, подвешенного
на пружине, от времени. Определить
амплитуду, период и частоту колебаний.
Записать уравнение колебанийНаписать уравнение гармонического колебания, если начальная фаза равна: 1)
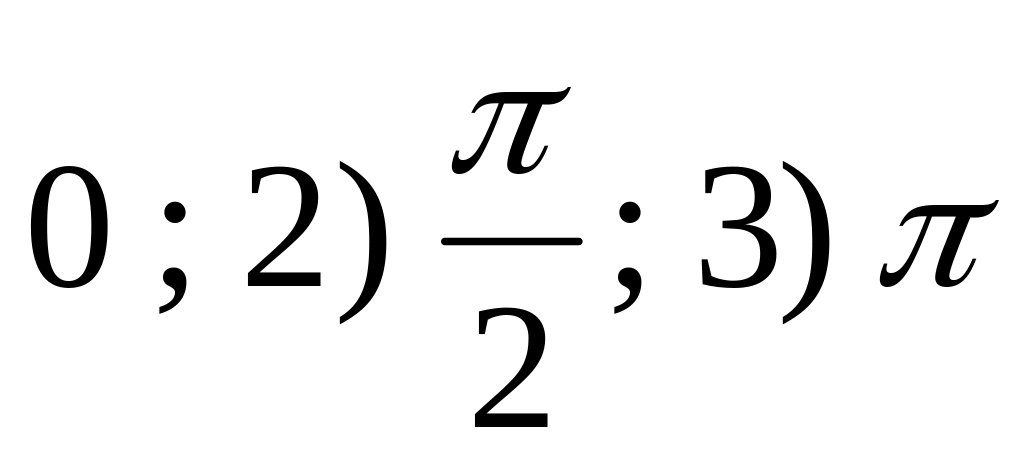 .
Амплитуда колебаний
.
Амплитуда колебаний
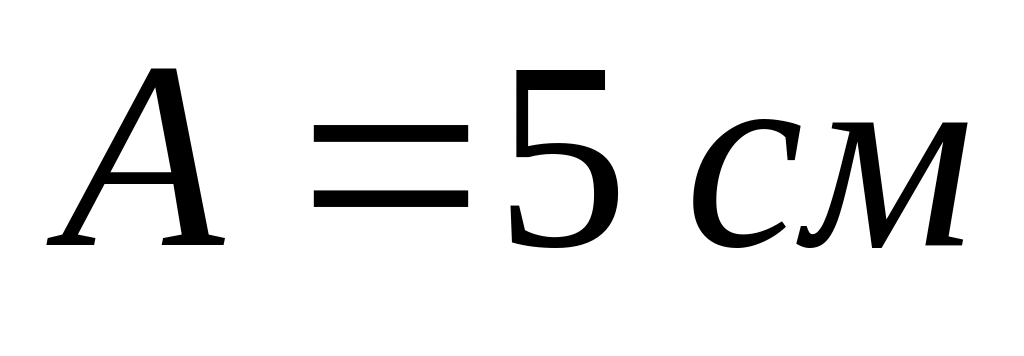 и период колебаний
и период колебаний
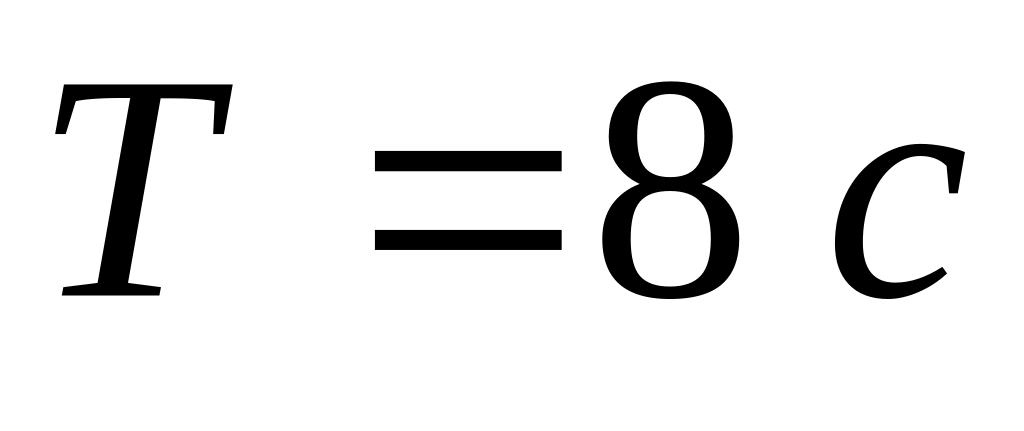 .
.Начертить на одном графике два гармонических колебания с одинаковыми амплитудами
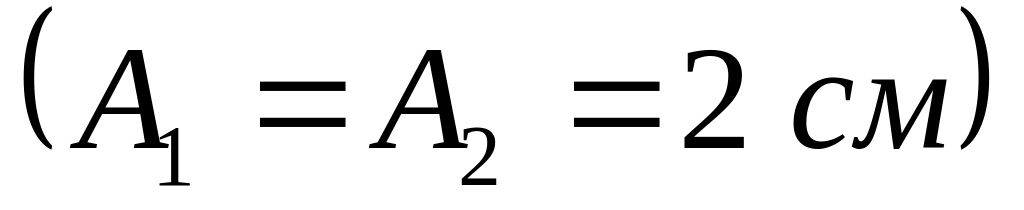 и одинаковыми периодами
и одинаковыми периодами
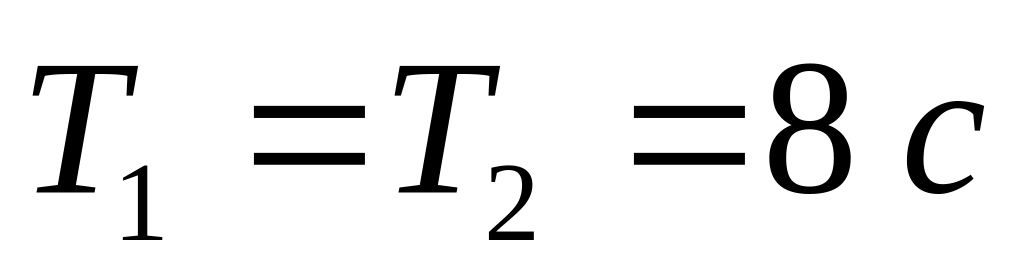 ,
но имеющими разность фаз:
,
но имеющими разность фаз:
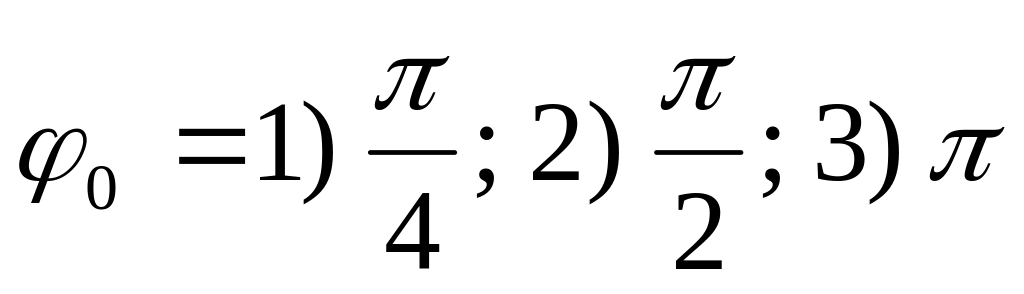 .
.Через сколько времени от начала движения точка, совершающая гармонические колебания, будет иметь смещение от положения равновесия, равное половине амплитуды? Период колебаний равен 24 с, начальная фаза равна нулю.
Через сколько времени от начала движения точка, совершающая гармонические колебания по закону
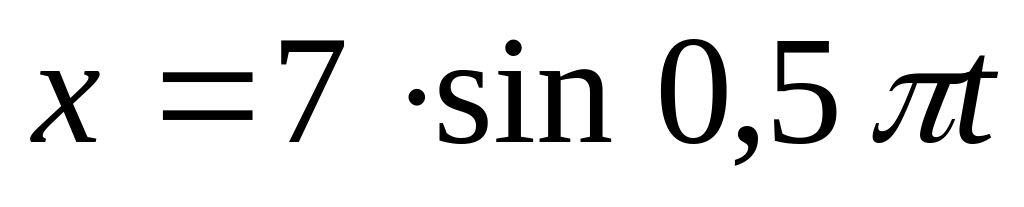 , проходит путь от положения равновесия
до максимального смещения?
, проходит путь от положения равновесия
до максимального смещения?Уравнение движения точки дано в виде
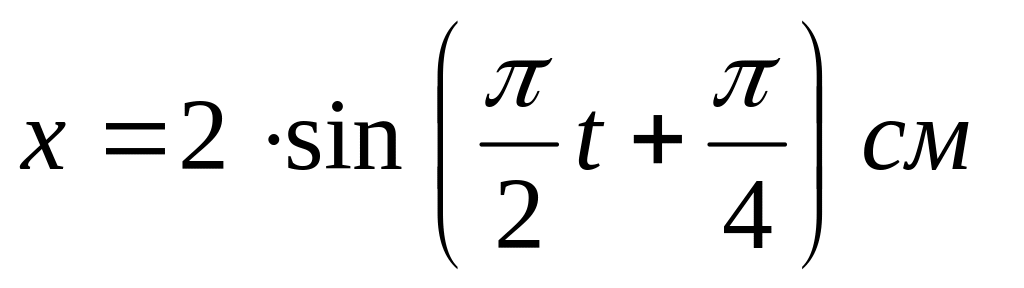 .
Найти: 1) период колебаний; 2) максимальную
скорость точки; 3) ее максимальное
ускорение.
.
Найти: 1) период колебаний; 2) максимальную
скорость точки; 3) ее максимальное
ускорение.Точка совершает гармонические колебания. Период колебаний равен 2 с, амплитуда 50 мм, начальная фаза равна нулю. Найти скорость точки в момент времени, когда смещение точки от положения равновесия равно 25 мм.
Уравнение колебаний материальной точки массой
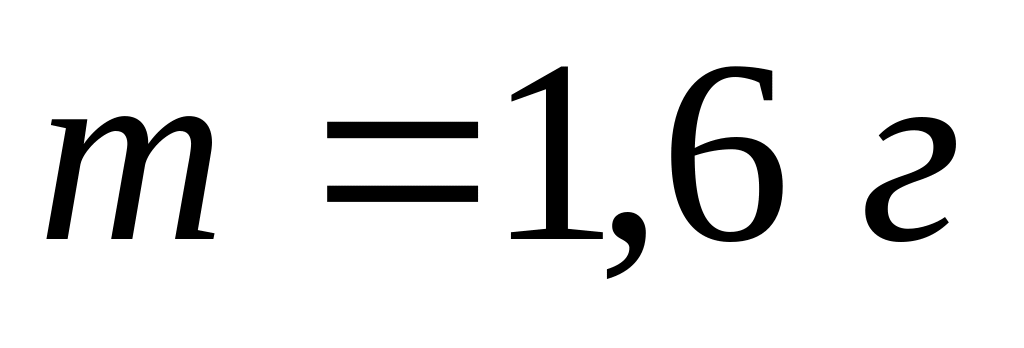 имеет вид
имеет вид
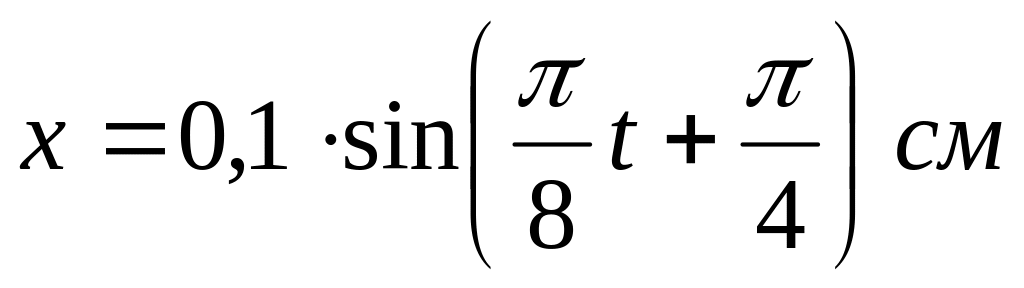 .
Построить график зависимости от времени
в пределах одного периода силы,
действующей на точку. Найти значение
максимальной силы.
.
Построить график зависимости от времени
в пределах одного периода силы,
действующей на точку. Найти значение
максимальной силы.Максимальная скорость точки, совершающей гармонические колебания, равна
 ,
максимальное ускорение
,
максимальное ускорение
 .
Найти угловую частоту колебаний, период
и амплитуду колебаний. Написать уравнение
колебаний, приняв начальную фазу равной
нулю.
.
Найти угловую частоту колебаний, период
и амплитуду колебаний. Написать уравнение
колебаний, приняв начальную фазу равной
нулю.Частица совершает гармонические колебания вдоль оси х около положения равновесия х=0. Частота колебаний
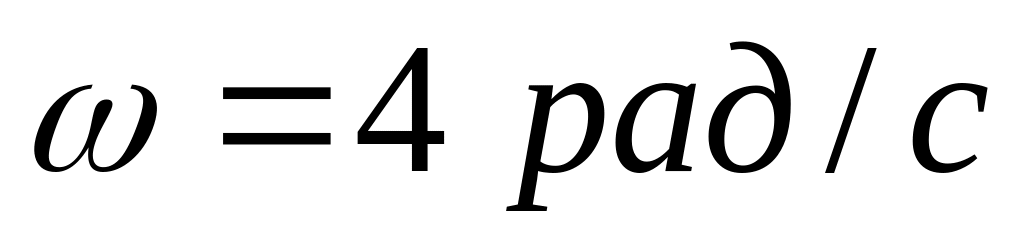 .
В некоторый момент времени координата
частицы
.
В некоторый момент времени координата
частицы
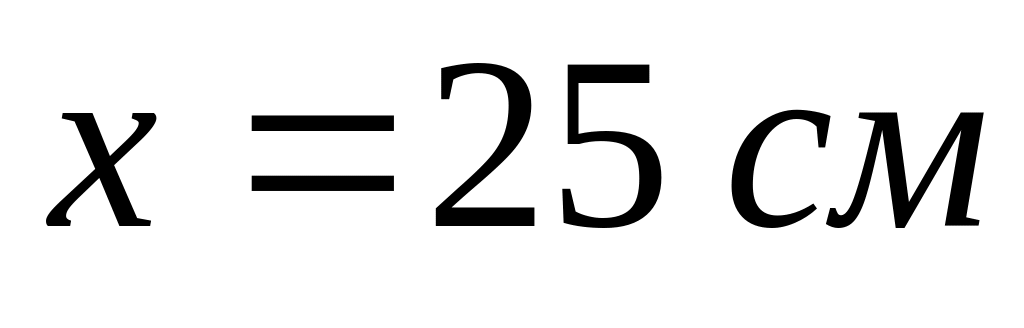 ,
а ее скорость
,
а ее скорость
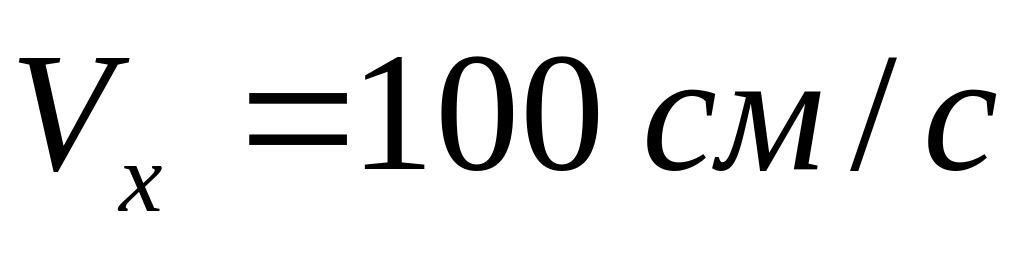 .
Найти координату частицы и ее скорость
через 2,4 с после этого момента.
.
Найти координату частицы и ее скорость
через 2,4 с после этого момента.Точка совершает гармонические колебания. Наибольшее смещение точки равно 10 см, наибольшая скорость 20 см/с. Найти угловую частоту колебаний и максимальное ускорение точки.
Точка совершает колебания по закону
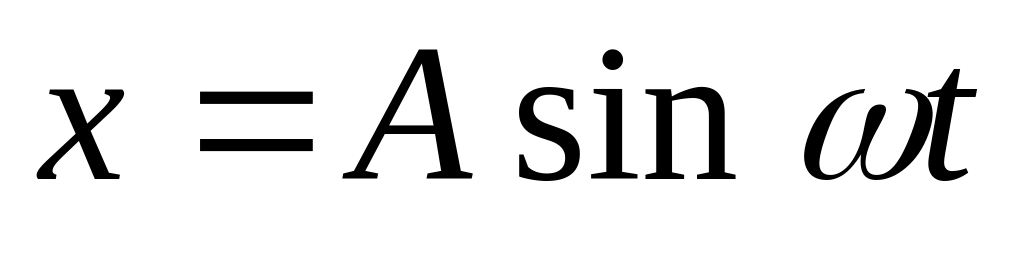 .
В некоторый момент времени смещение
точки оказалось равным 5 см. Когда фаза
колебаний увеличилась вдвое, смещение
стало равным 8 см. Найти амплитуду
колебаний.
.
В некоторый момент времени смещение
точки оказалось равным 5 см. Когда фаза
колебаний увеличилась вдвое, смещение
стало равным 8 см. Найти амплитуду
колебаний.Тело совершает гармонические колебания с периодом
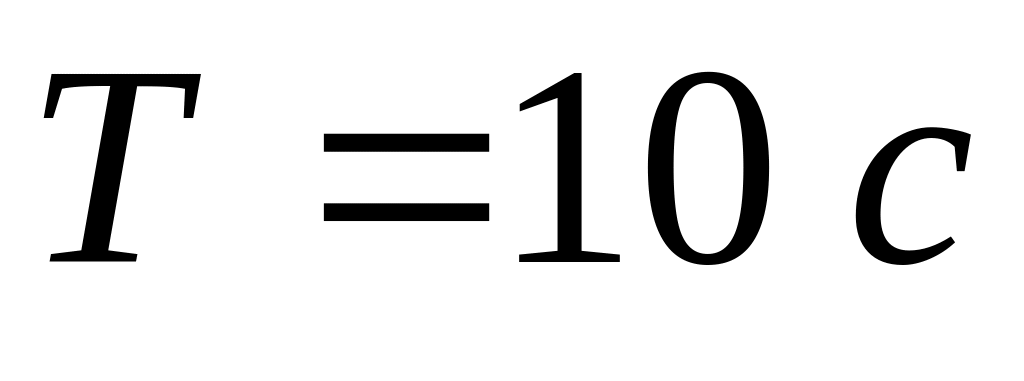 .
За какое время тело проходит весь путь
от среднего положения до крайнего?
.
За какое время тело проходит весь путь
от среднего положения до крайнего?
При гармонических колебаниях вдоль оси ОХ координата тела меняется по закону
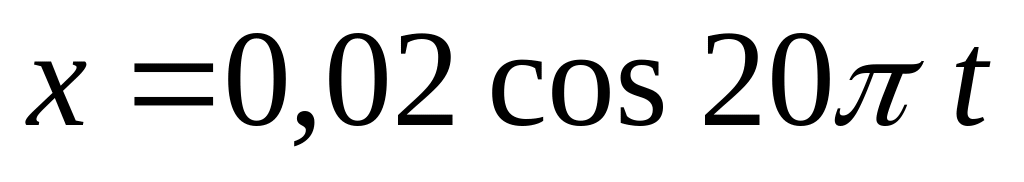 .
Чему равна частота колебаний ускорения
тела?
.
Чему равна частота колебаний ускорения
тела?Тело совершает гармонические колебания по закону
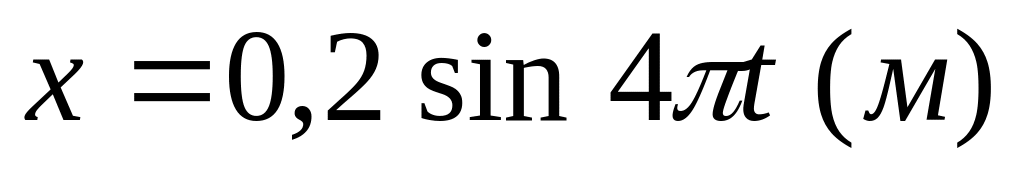 .
Период и частота колебаний равны
.
Период и частота колебаний равныОпределите полную энергию материальной точки массой m, колеблющейся по закону
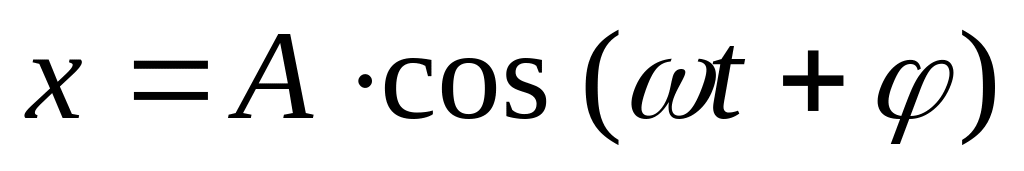 .
.Полная энергия тела, совершающего гармонические колебания равна
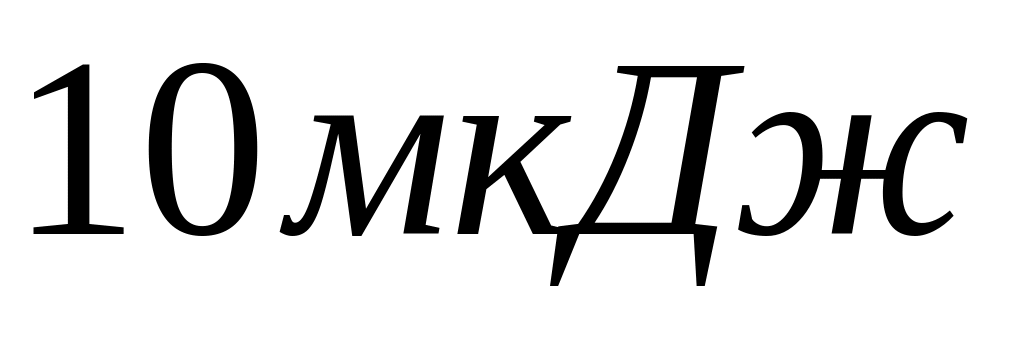 ,
а максимальная сила, действующая на
точку- равна 0,5 мН. Напишите уравнение
движения точки, если период колебаний
равен 4 с, а начальная фаза колебаний
,
а максимальная сила, действующая на
точку- равна 0,5 мН. Напишите уравнение
движения точки, если период колебаний
равен 4 с, а начальная фаза колебаний
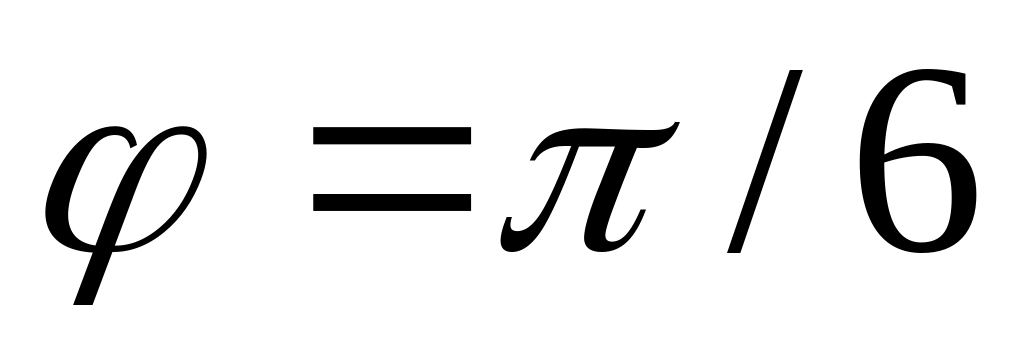 .
.Материальная точка массой 50 г совершает колебания, уравнение которых имеет вид
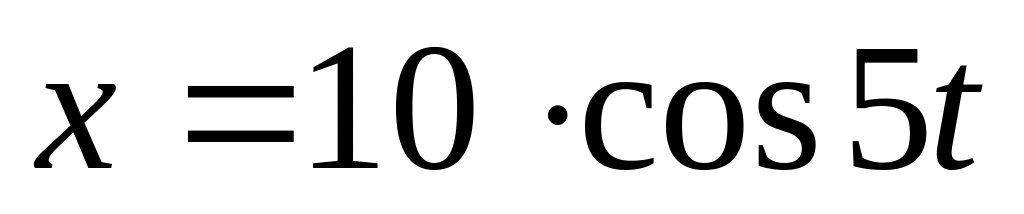 .
Найти силу, действующую на точку в
момент, когда фаза
.
Найти силу, действующую на точку в
момент, когда фаза
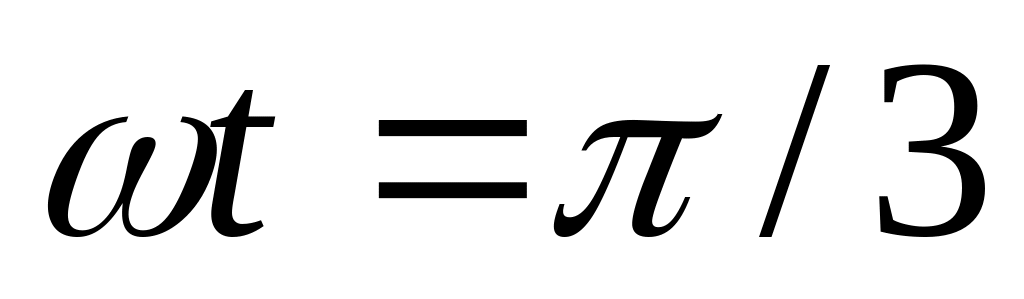 .
.Колебания материальной точки массой 0,1 кг происходят согласно уравнению
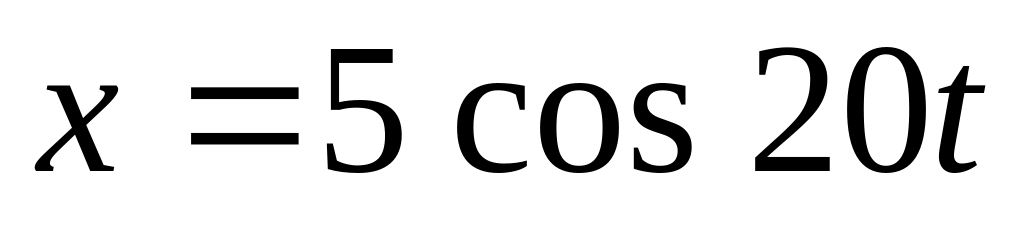 .
Определите максимальное значение
возвращающей силы и максимальное
значение кинетической энергии.
.
Определите максимальное значение
возвращающей силы и максимальное
значение кинетической энергии.
