
- •Вопросы и упражнения
- •Семинар 2 Кинематика вращательного движения
- •Вопросы и упражнения
- •Семинар 3 Движение тел под действием силы тяжести
- •Вопросы и упражнения
- •Задачи Свободное падение. Движение тела, брошенного вертикально вверх
- •Движение тела, брошенного горизонтально
- •Движение тела, брошенного под углом к горизонту
- •Семинар 4 Динамика материальной точки и тела, движущихся поступательно
- •Вопросы и упражнения
- •Семинар 5 Силы в механике
- •Вопросы и упражнения
- •Семинар 7 работа. Мощность. Энергия. Закон сохранения энергии
- •Вопросы и упражнения
- •Семинар 8 Моменты инерции твердых тел
- •Вопросы и упражнения
- •Семинар 9 динамика вращательного движения твердого тела относительно неподвижной оси
- •Вопросы и упражнения
- •Семинар 10 законы сохранения. Закон сохранения момента импульса
- •Вопросы и упражнения
- •Семинар 11 Кинематика колебаний
- •Вопросы и упражнения
- •Семинар 12 Математический , пружинный и физический маятник
- •Задания и упражнения
- •Физический маятник
- •Семинар 14 Сложение колебаний
- •Вопросы и упражнения
- •Семинар 14 элементы механики жидкости
- •Вопросы и упражнения
- •З адачи
- •Семинар 15 Основы теории относительности
Самарский государственный университет
Задания
к практическим занятиям по механике
для студентов химического факультета
В.А.Жукова
Самара 2013
Семинар 1
Кинематика поступательного движения. Средняя скорость.
О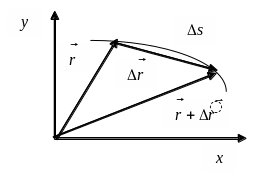 сновные
формулы
сновные
формулы
Положение
материальной точки в пространстве в
момент времени
![]() определяется радиус-вектором
определяется радиус-вектором
![]() (рис.1)
(рис.1)
Средняя
скорость
![]()
Средняя
путевая скорость
![]() ,
где
,
где
![]() -путь,
пройденный точкой за интервал времени
-путь,
пройденный точкой за интервал времени
![]() .
.
Мгновенная
скорость
![]()
В
декартовой системе координат
![]() ,
,
Модуль
вектора перемещения
![]()
Тогда
скорость
![]() ,
,
Следовательно
компоненты скорости даются формулами
![]()
Модуль
вектора скорости
![]()
Мгновенное
ускорение
![]() ,
,
компоненты
ускорения могут быть выражены
![]()
модуль
вектора ускорения
![]()
Вопросы и упражнения
Что изучает механика как один из разделов физики?
Что такое тело отсчета?
Что такое система отсчета?
Что такое радиус-вектор?
Дайте определения кинематических величин: перемещения, пройденного пути, средней скорости, мгновенной скорости, среднего ускорения, мгновенного ускорения. В каких единицах измеряются эти величины?
Как ориентированы векторы скорости (мгновенной и средней) и ускорения относительно траектории и друг друга?
Какое движение абсолютно твердого тела называется поступательным?
Как можно вычислить пройденный путь, если задан график зависимости скорости от времени?
Приведите примеры, когда Землю можно представить как материальную точку и когда этого сделать нельзя.
Как найти результирующее перемещение точки, если известны составляющие перемещения, в которых она участвует?
Какие Вам известны способы задания законов движения?
ЗАДАЧИ
Автомобиль половину пути движется со скоростью
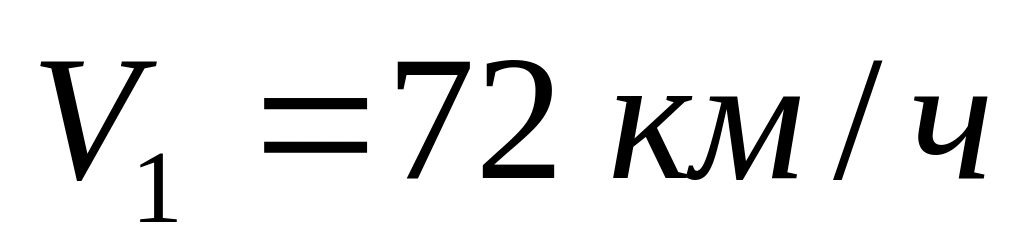 ,
а вторую половину пути – со скоростью
,
а вторую половину пути – со скоростью
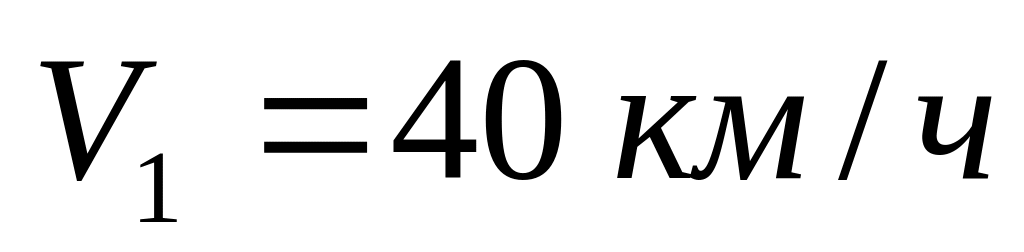 .
Найти среднюю путевую скорость
автомобиля.
.
Найти среднюю путевую скорость
автомобиля.
Автомобиль половину времени движется со скоростью , а вторую половину времени – со скоростью . Найти среднюю путевую скорость автомобиля.
Положение материальной точки на оси х в зависимости от времени задано уравнением
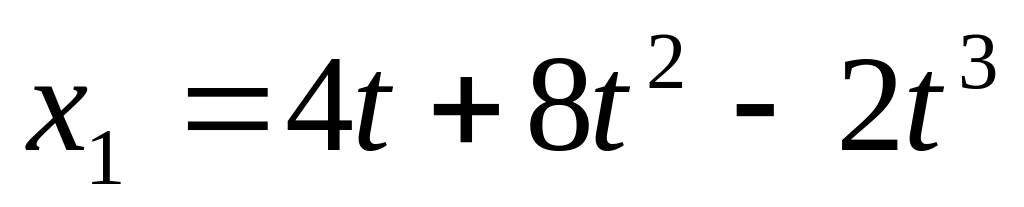 .
Найти среднюю скорость точки на временном
интервале от
.
Найти среднюю скорость точки на временном
интервале от
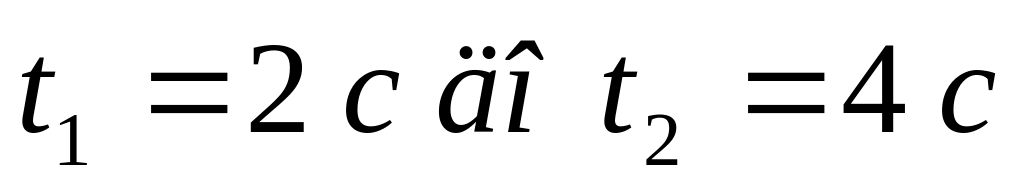 .
Сравнить полученное значение с
мгновенными скоростями
.
Сравнить полученное значение с
мгновенными скоростями
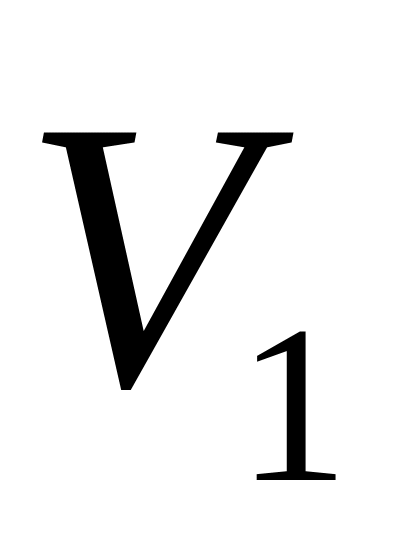 и
и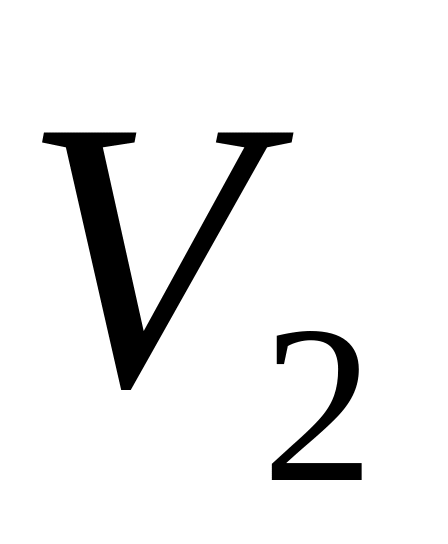 в моменты времени
в моменты времени
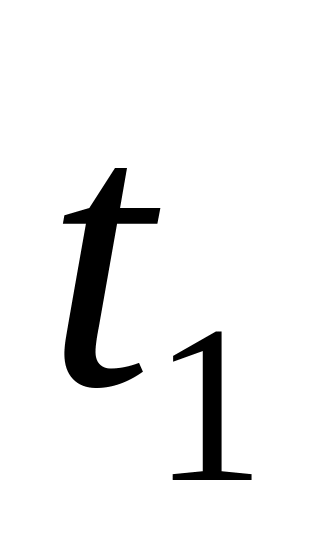 и
и
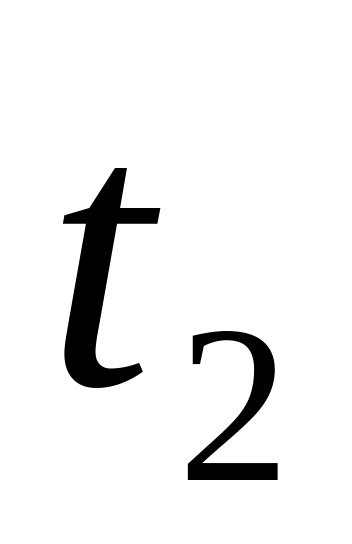 соответственно.
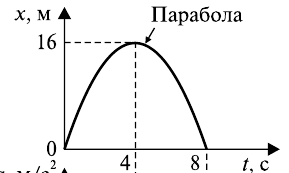
соответственно.Кинематическое уравнение движения материальной точки по прямой имеет вид
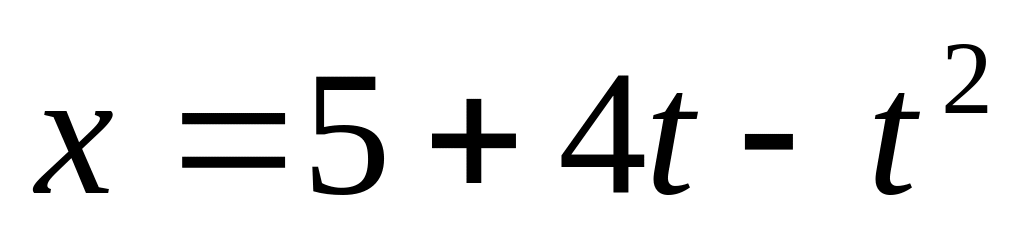 .
Найти: 1) максимальное значение координаты;
2)момент времени, когда точка возвращается
в то же место, где она была в начальный
момент времени. Построить график
зависимости от времени координаты и
пути, пройденного точкой с момента
.
Найти: 1) максимальное значение координаты;
2)момент времени, когда точка возвращается
в то же место, где она была в начальный
момент времени. Построить график
зависимости от времени координаты и
пути, пройденного точкой с момента
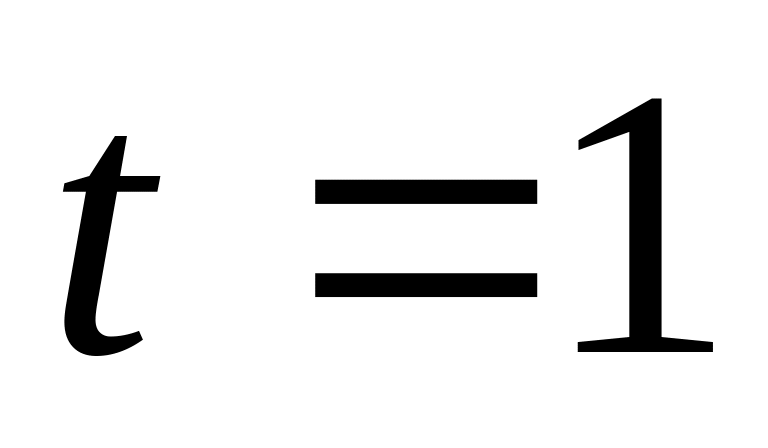 до
до
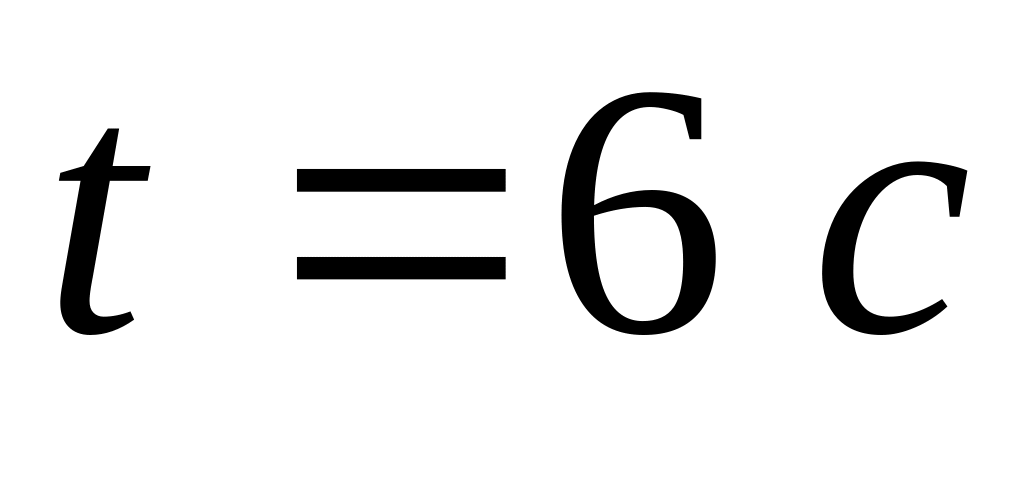 .
.М
 атериальная
точка движется в плоскости согласно
уравнениям
атериальная
точка движется в плоскости согласно
уравнениям
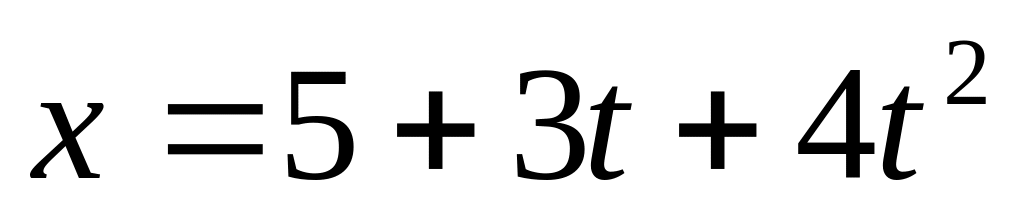 и
и
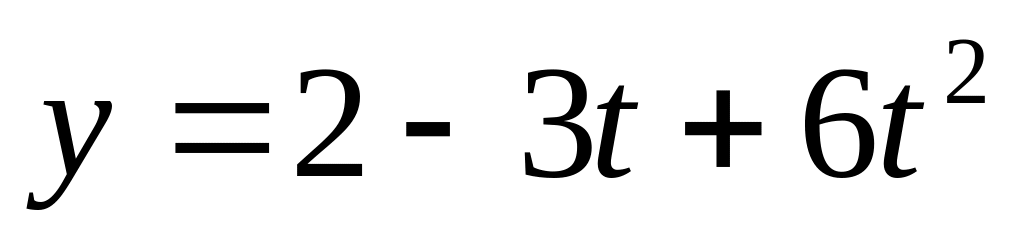 .
Найти модули скорости и ускорения точки
в момент времени
.
Найти модули скорости и ускорения точки
в момент времени
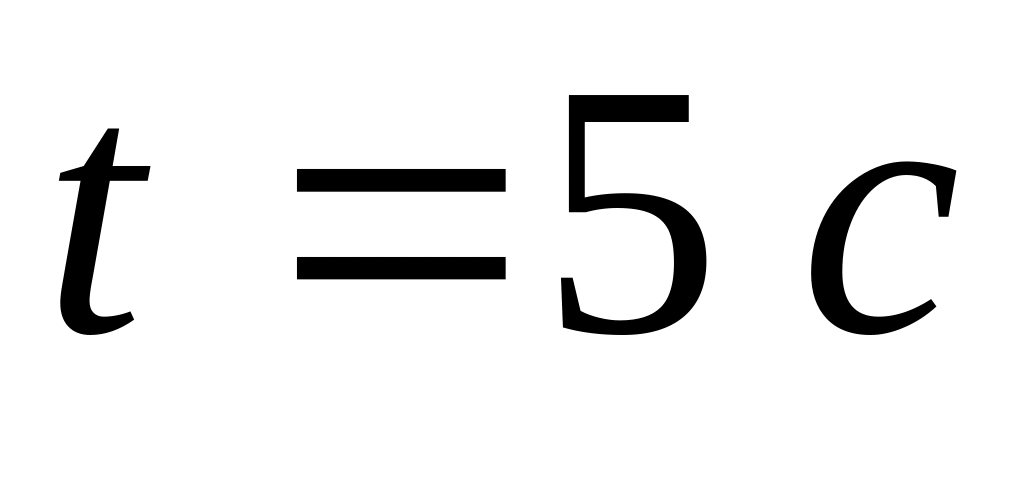
Точка движется вдоль оси х согласно графику, изображенному на рисунке. Построить графики изменения ускорения и скорости движения. Определить начальную и среднюю скорость движения.
Материальная точка движется прямолинейно с начальной скоростью
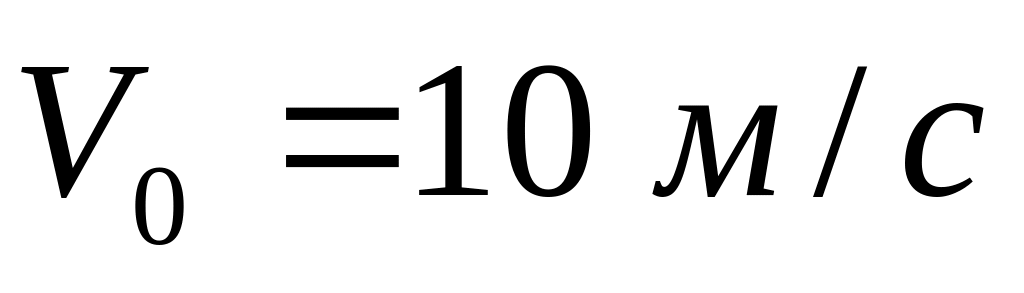 и с постоянным ускорением
и с постоянным ускорением
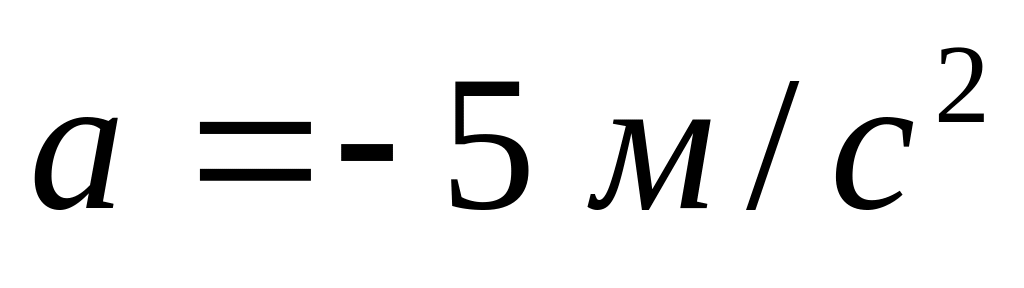 .
Определить, чему равен путь, пройденный
точкой, и модуль ее перемещения спустя
4 с после начала движения.
.
Определить, чему равен путь, пройденный
точкой, и модуль ее перемещения спустя
4 с после начала движения.Автомобиль едет по прямой из пункта А в пункт В, преодолевая это расстояние за
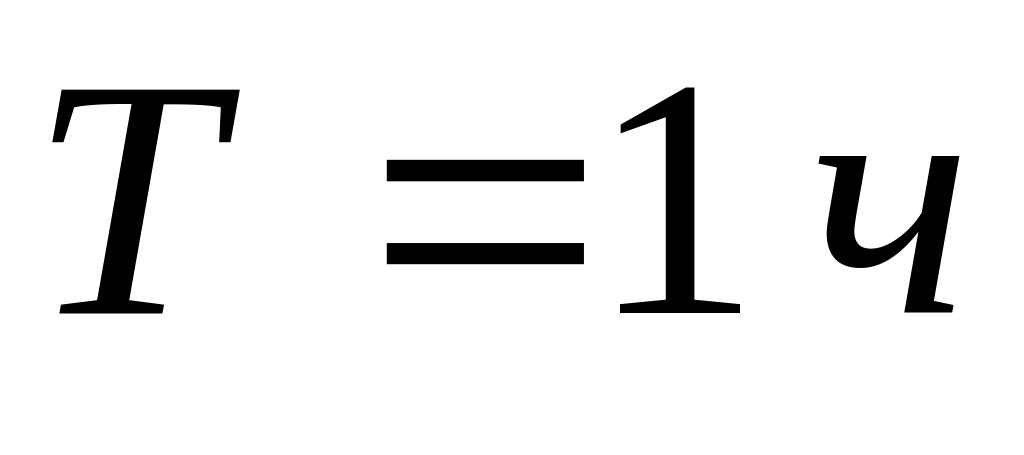 .
Известно, что скорость автомобиля
меняется по закону
.
Известно, что скорость автомобиля
меняется по закону
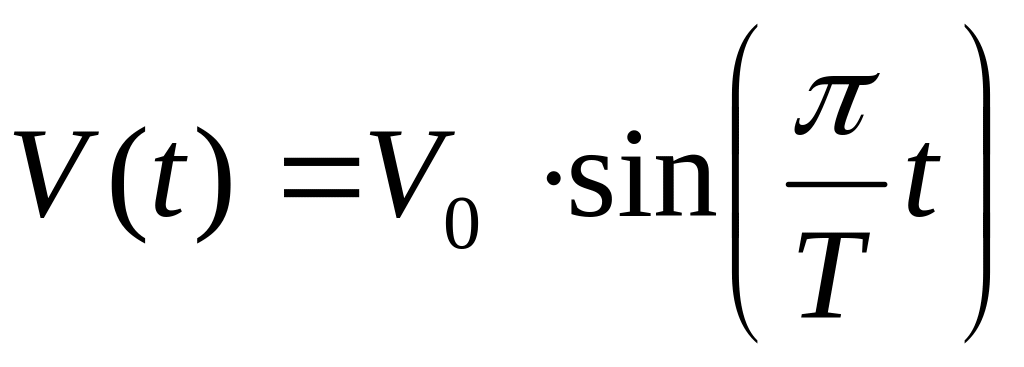 ,
где время t отсчитывается с момента
выезда из пункта А, а максимальная
скорость автомобиля
,
где время t отсчитывается с момента
выезда из пункта А, а максимальная
скорость автомобиля
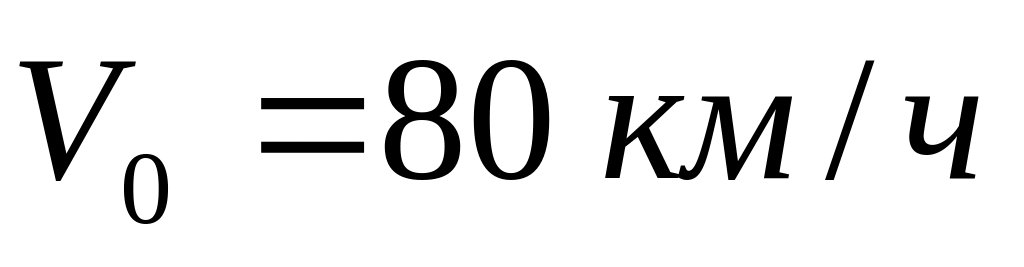 .
Определить среднюю путевую скорость
автомобиля и расстояние между пунктами
А и В.
.
Определить среднюю путевую скорость
автомобиля и расстояние между пунктами
А и В.Скорость реки
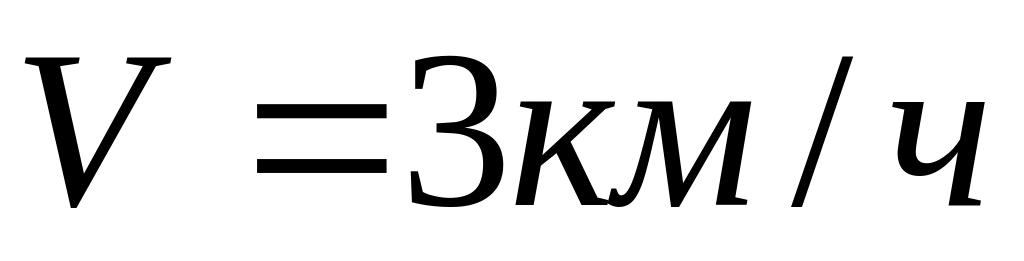 ,
а скорость движения лодки относительно
воды
,
а скорость движения лодки относительно
воды
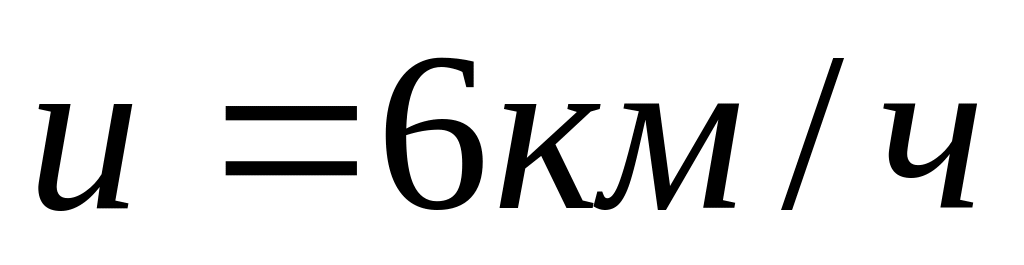 .
Определить, под каким углом относительно
берега должна двигаться лодка, чтобы
проплыть поперек реки.
.
Определить, под каким углом относительно
берега должна двигаться лодка, чтобы
проплыть поперек реки.Капля дождя при скорости ветра
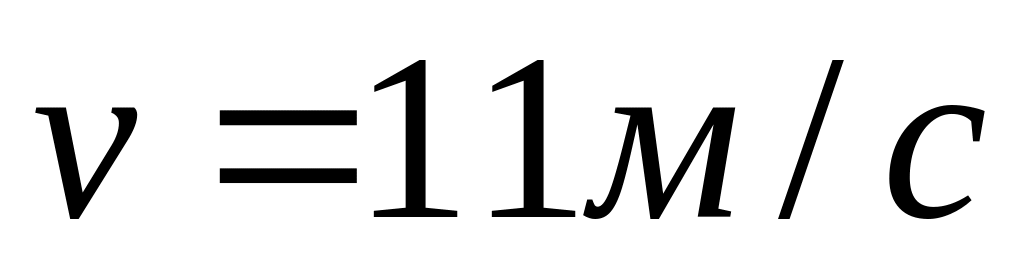 падает под углом
падает под углом
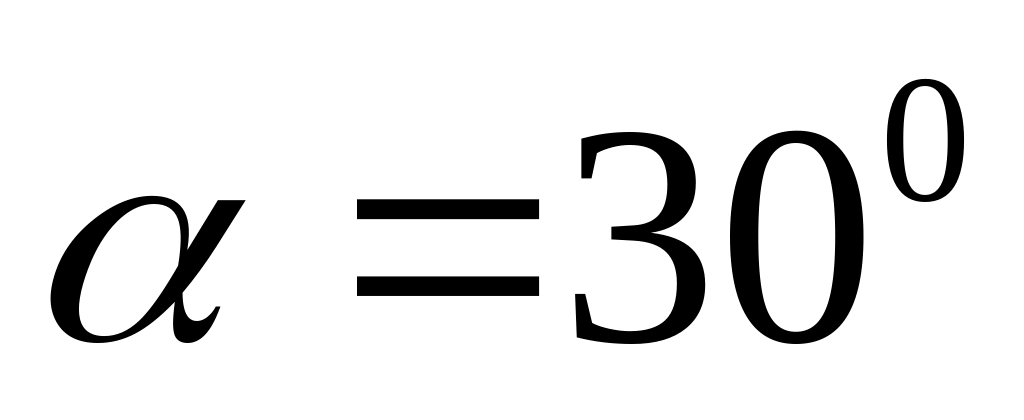 к вертикали. Определите, при какой
скорости ветра капля воды будет падать
под углом
к вертикали. Определите, при какой
скорости ветра капля воды будет падать
под углом
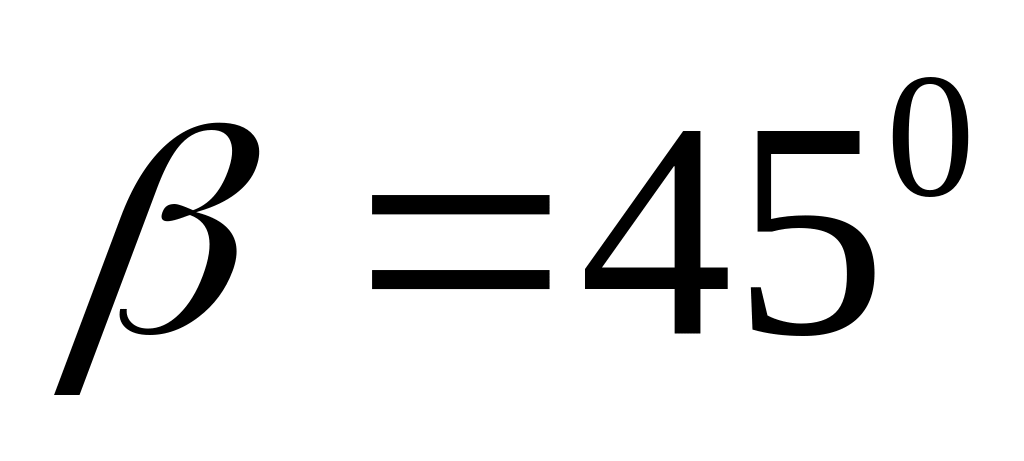 .
.Два автомобиля, выехав одновременно из одного пункта, движутся прямолинейно в одном направлении. Зависимость пройденного пути дается уравнениями
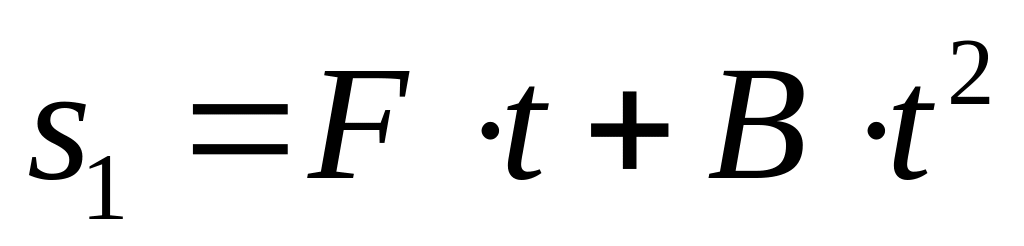 и
и
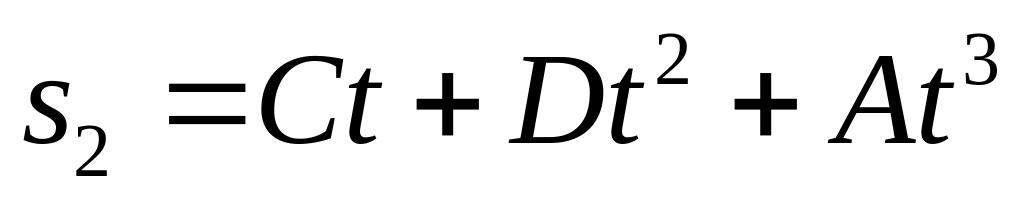 .
Определите относительную скорость
автомобилей.
.
Определите относительную скорость
автомобилей.Автомобиль проехал первую половину времени своего движения со скоростью
 ,
вторую половину времени своего движения
– со скоростью
,
вторую половину времени своего движения
– со скоростью
 Определите среднюю скорость движения
автомобиля.
Определите среднюю скорость движения
автомобиля.
Автомобиль проехал первую половину пути своего движения со скоростью , вторую половину пути своего движения – со скоростью Определите среднюю скорость движения автомобиля.
В течение времени
 скорость задается уравнением вида
скорость задается уравнением вида
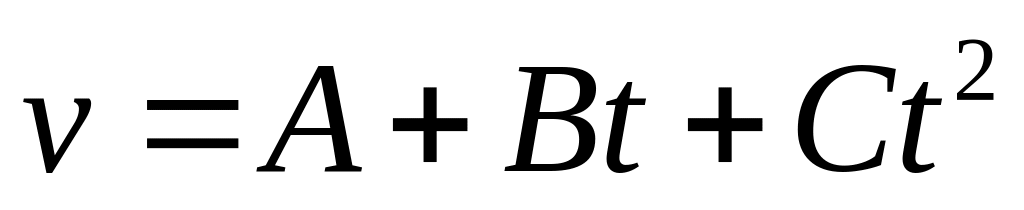 .
Определить среднюю скорость за указанный
промежуток времени.
.
Определить среднюю скорость за указанный
промежуток времени.Материальная точка движется по плоскости согласно уравнению
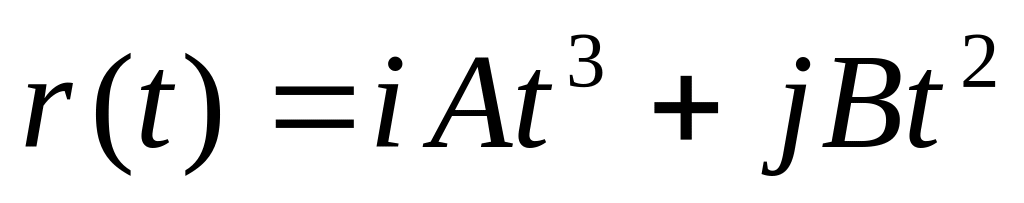 .
Написать зависимости :
.
Написать зависимости :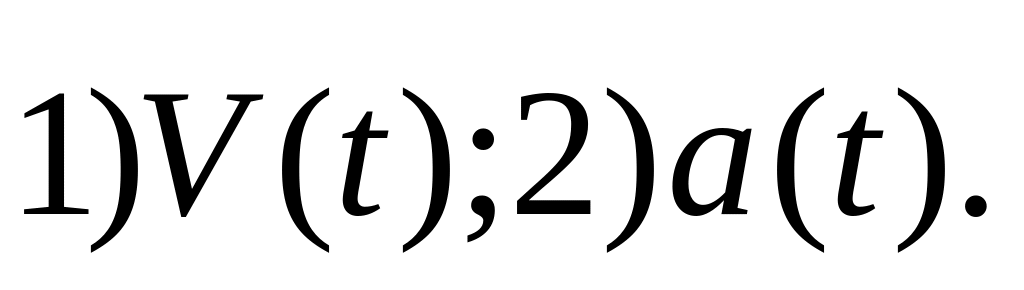
Движение точки по прямой задано уравнением
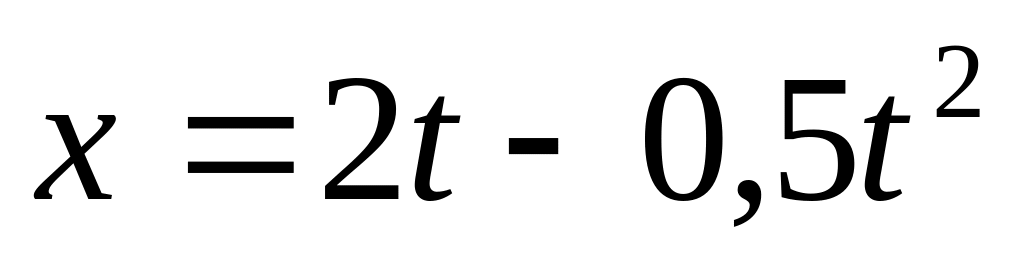 .
Определить среднюю скорость движения
точки в интервале времени от t1=1
c
до t2=3
c.
.
Определить среднюю скорость движения
точки в интервале времени от t1=1
c
до t2=3
c.Частица движется в плоскости х,у из точки с координатами х=у=0 со скоростью
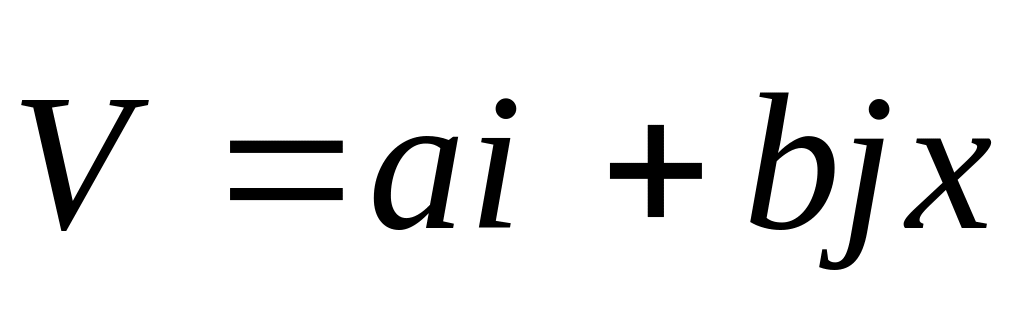 ,
где а и b
– некоторые постоянные. Найти уравнение
её траектории.
,
где а и b
– некоторые постоянные. Найти уравнение
её траектории.
Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид . Построить график зависимости координаты х и пути от времени. Определить среднюю скорость за интервал времени от 1 с до 6 с.
Движение материальной точки в плоскости ху описывается законом
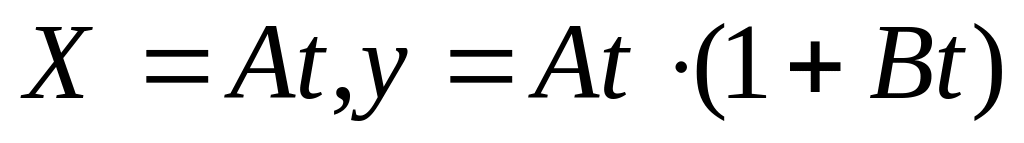 ,
где А и В – положительные постоянные.
Определите: 1) уравнение траектории; 2)
радиус-вектор точки в зависимости от
времени; 3) скорость точки в зависимости
от времени; 4) ускорение точки в зависимости
от времени.
,
где А и В – положительные постоянные.
Определите: 1) уравнение траектории; 2)
радиус-вектор точки в зависимости от
времени; 3) скорость точки в зависимости
от времени; 4) ускорение точки в зависимости
от времени.Зависимость пройденного телом пути
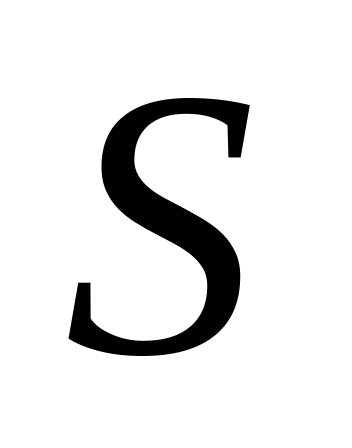 от
времени
от
времени
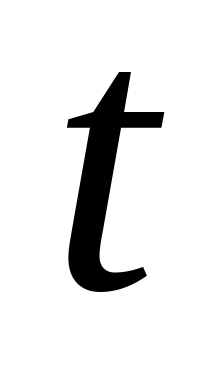 дается уравнением
дается уравнением
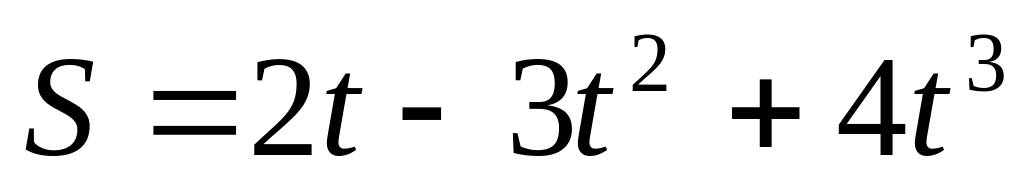 .
Найти: 1) зависимость скорости и ускорения
от времени; 2) расстояние, пройденное
телом, скорость и ускорение через 2 с
после начала движения
.
Найти: 1) зависимость скорости и ускорения
от времени; 2) расстояние, пройденное
телом, скорость и ускорение через 2 с
после начала движенияКинематические уравнения движения двух материальных точек имеют вид: x1=-2t2 , x2=2t+t3. Определить момент времени, для которого ускорения этих точек будут равны.
Зависимость пройденного точкой пути от времени задана уравнением
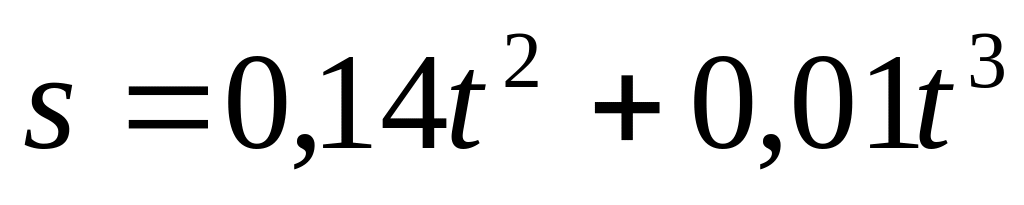 ( здесь и далее, если не оговорено особо,
время измеряется в секундах, расстояние
в метрах. Определить: 1) через какое
время ускорение точки будет равно
( здесь и далее, если не оговорено особо,
время измеряется в секундах, расстояние
в метрах. Определить: 1) через какое
время ускорение точки будет равно
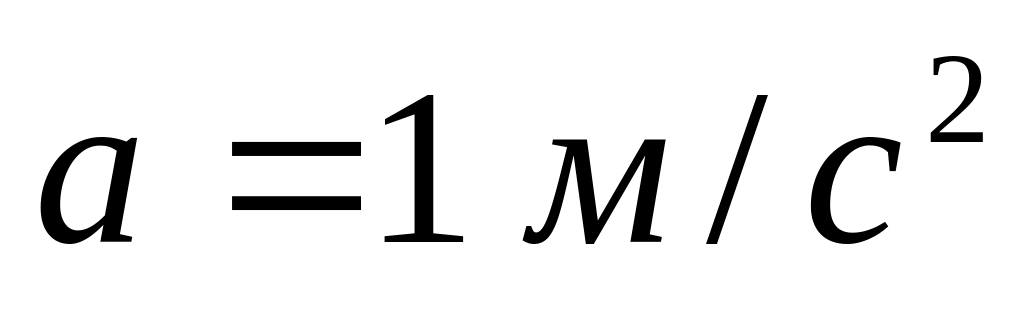 ;
2) мгновенную скорость в этот момент
времени; 3) среднюю путевую
скорость за промежуток времени от
;
2) мгновенную скорость в этот момент
времени; 3) среднюю путевую
скорость за промежуток времени от
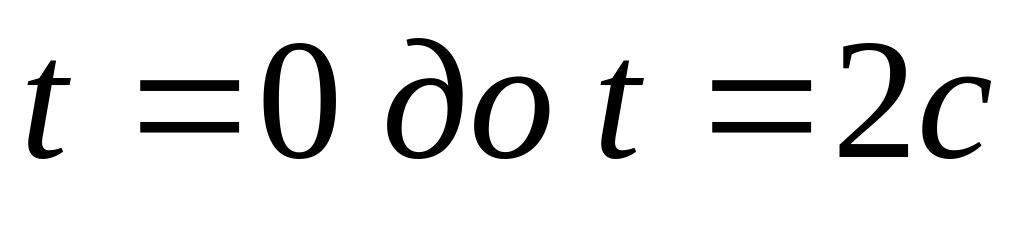 .
.Положение точки на прямой в зависимости от времени дается уравнением
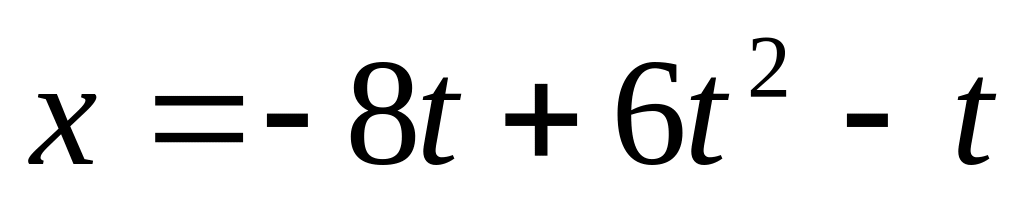 .
Сравнить ее со средними скоростями
.
Сравнить ее со средними скоростями
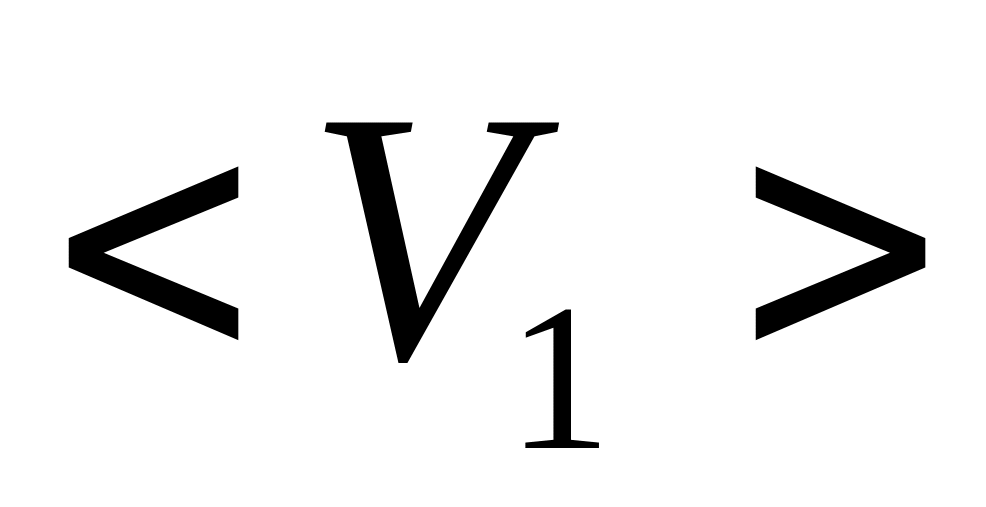 на интервале от
на интервале от
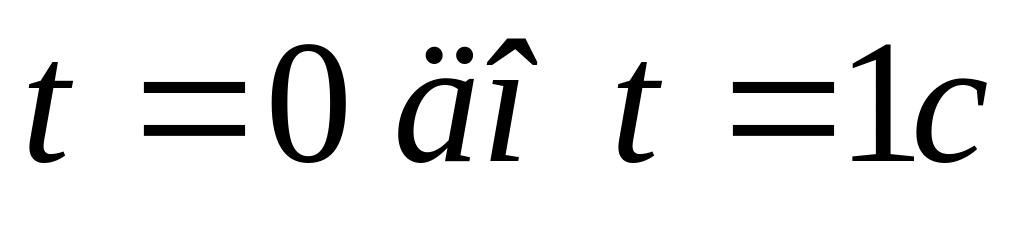 и
и
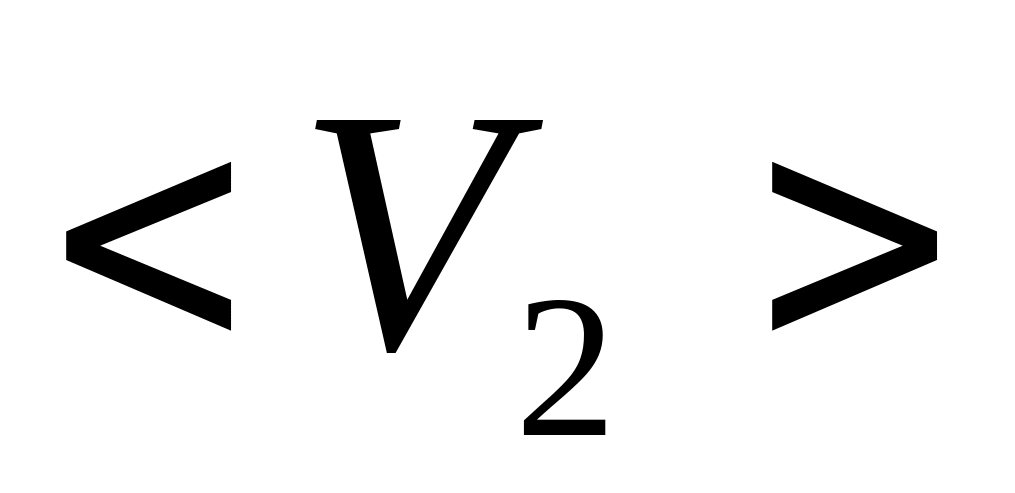 на интервале
на интервале
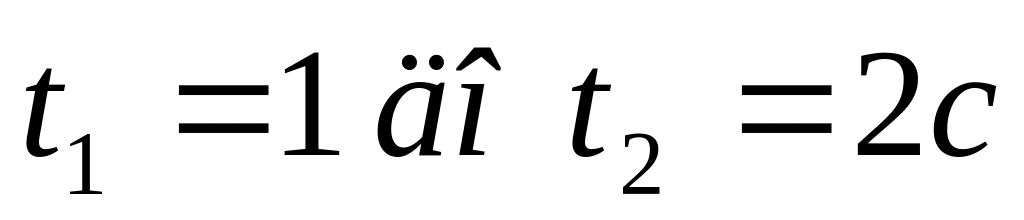 .
.Две материальные точки движутся согласно уравнениям
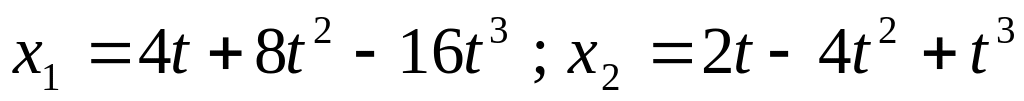 .
В какой момент времени ускорения этих
тел будут одинаковы? Найти скорости
точек в этот момент времени.
.
В какой момент времени ускорения этих
тел будут одинаковы? Найти скорости
точек в этот момент времени.Движение двух материальных точек заданы уравнениями
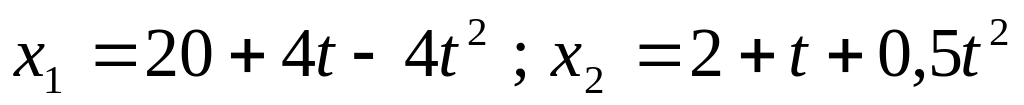 .
В какой момент времени скорости этих
точек будут одинаковы? Определить
скорости и ускорения точек в этот
момент.
.
В какой момент времени скорости этих
точек будут одинаковы? Определить
скорости и ускорения точек в этот
момент.Зависимость пройденного телом пути от времени дается уравнением
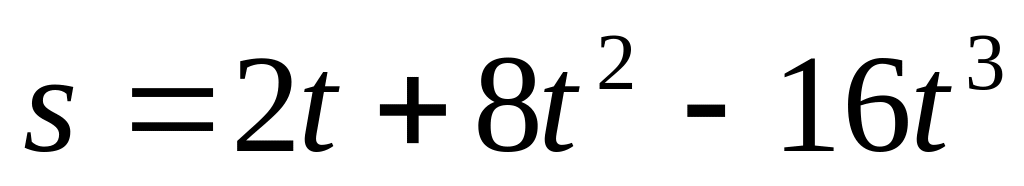 .
Найти расстояние, пройденное телом,
скорость и ускорение тела через 2 с
после начала движения.
.
Найти расстояние, пройденное телом,
скорость и ускорение тела через 2 с
после начала движения.
