Задача 8

Задана выборка из некоторой генеральной совокупности, имеющей нормальное распределение:

xi	-0,26	-0,12	0,06	0,11	0,25	0,28	0,34	0,44	0,56	1,12
ni	1	41	21	31	1	11	1	1	1	1

Найти выборочное среднее и несмещенную оценку генеральной дисперсии.

Решение

Несмещенной оценкой генеральной средней является выборочная средняя ( ):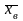

. (8.1)

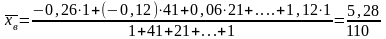= 0,048.

Несмещенной оценкой генеральной дисперсии является исправленная выборочная дисперсия (s²):

. (8.2)

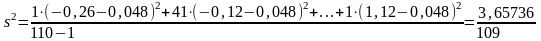= 0,034.

Ответ: 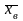= 0,048; s² = 0,034.

Задача 9

По результатам 65 измерений случайной величины, имеющей нормальное распределение с дисперсией 0,94 см², получено значение выборочного среднего 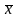= 1,5 см. Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а генеральной совокупности.

Решение

Для оценки математического ожидания а случайной величины х, распределенной по нормальному закону, при известном среднем квадратическом отклонении σ служит доверительный интервал:

, (9.1)

где 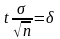– точность оценки;

n – объем выборки;

х^* – выборочное среднее;

t – аргумент функции Лапласа, при котором .

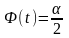Все величины, кроме t, известны. Найдем t из соотношения:

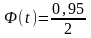= 0,75.

По специальной таблице определяем значение t = 1,96.

Далее находим доверительный интервал по формуле 9.1.

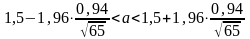
Ответ: .

Задача 10

Имеются данные о личных доходах Х 8 семей и их расходах на питание Y. Требуется:

а) найти выборочный коэффициент корреляции;

б) проверить гипотезу о значимости коэффициента корреляции;

в) составить уравнение регрессии Y на Х;

г) составить уравнение регрессии Х на Y;

д) построить прямые регрессии.

xi	30	32	42	52	62	64	65	69
yi	21	25	36	45	56	60	61	62

Решение

Для определения вида зависимости построим корреляционное поле (рисунок 10.1).

Рисунок 10.1 – Корреляционное поле

По расположению точек на корреляционном поле полагаем, что зависимость между х и у линейная:

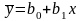
Для нахождения уравнения регрессии построим таблицу.

i	xi	yi	xi2	yi2	xiyi		ei	ei2
1	20	21	900	441	630	24	-3	9
2	32	25	1024	625	800	26	-1	1
3	42	36	1764	1296	1512	36	0	0
4	52	45	2704	2025	2340	46	-1	1
5	62	56	3844	3136	3472	56	0	0
6	64	60	4096	3600	3840	58	2	4
7	65	61	4225	3721	3965	59	2	4
8	69	62	4761	3844	4278	63	-1	1
сумма	416	366	23318	18688	20837	368	-	-
среднее	52	46	2915	2336	2605	46	-	-

По методу наименьших квадратов имеем:

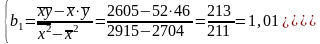. (10.1)

Таким образом, уравнение регрессии Y на X имеет вид:

. (10.2)

А уравнение регрессии Х на Y имеет вид:

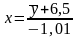. (10.3)

Построим данные регрессии на графиках (рисунок 10.2 и 10.3).

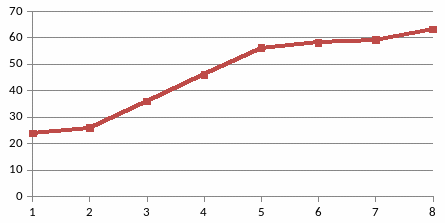
Рисунок 10.2 – Прямая регрессии Y на X

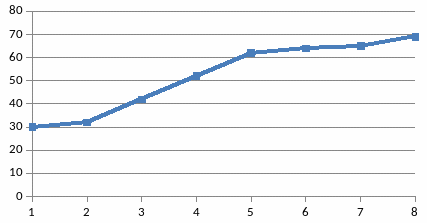
Рисунок 10.2 – Прямая регрессии X на Y

Далее для расчета коэффициента корреляции рассчитаем и е_i, используя формулу:

. (10.4)

Для анализа силы линейной зависимости вычислим коэффициент корреляции (методом Пирсона):

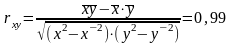. (10.5)

Данное значение коэффициента корреляции позволяет сделать вывод о сильной (прямой) линейной зависимости между рассматриваемыми переменными х и у. Это также подтверждается расположением точек на корреляционном поле.

Значимость коэффициентов корреляции оцениваем при помощи критерия Стьюдента по формуле:

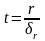, (10.6)

где 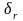- среднеквадратическая ошибка коэффициента корреляции, которая определяется по формуле:

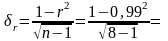0,27. (10.7)

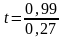= 3,6.

Т.к. расчетная величина 3,6 > 0,1, то можно сделать заключение о том, что величина коэффициента корреляции является значимой.