Задача 1
Сколькими способами можно расположить в ряд 6 белых, 5 черных и 3 красных шара?
Решение
Для решения задачи воспользуемся формулой комбинаторики, которая гласит: перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле:
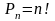(1.1)
В данной задаче 6 белых, 5 черных и 3 красных шара можно расположить в ряд:
=
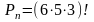90! =14.
Ответ: 14 способов.
Задача 2
Найти вероятность того, что среди 6 карт, наугад выбранных из колоды в 36 карт, имеются ровно две карты черной масти.
Решение
Так как первую карту черной масти можно извлечь из колоды 36 способами, а вторую – 35 (поскольку в колоде осталось 35 карт), то число возможных исходов опыта равно n:
=
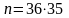1 260.
Далее определим число благоприятных исходов. Первую карту черной масти можно выбрать из 18 имеющихся (т,к, в колоде 18 карт черной масти и 18 - красной), вторую карту черной масти – соответственно уже из 17 карт. Значит, число благоприятных исходов равно m:
=
306.
Искомая вероятность (Р) того, что среди 6 карт, наугад выбранных из колоды в 36 карт, имеются ровно две карты черной масти, равна:
=
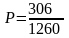0,243.
Ответ: Р = 0,243.
Задача 3
Вероятность попадания в цель при одном выстреле равна 0,82. Найти вероятность наивероятнейшего числа попаданий при 10 выстрелах.
Решение
Для решения воспользуемся формулой Бернулли для определения наивероятнейшего числа наступлений события (m0).
Число m0 называется наивероятнейшим числом наступлений события А в n испытаниях и равно целой части числа (n+1)·p.
Тогда, вероятность наивероятнейшего числа попаданий при 10 выстрелах, при вероятности попадания в цель при одном выстреле р = 0,82, составит:
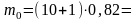9
раз.
Ответ: 9 раз.
Задача 4
Произведено 1 000 независимых испытаний с вероятностью наступления события А в отдельном испытании 0,01. Найти границы в которых с вероятностью 0,99 заключена относительная частота события А.
Решение
Поскольку условия опыта неизменны, то применяется схема независимых испытаний Бернулли.
Используется формула:
,
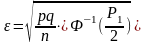(4.1)
В этой формуле:
–
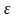величина
отклонения относительной частоты от
вероятности;
p = 0,01 – вероятность появления события А в одном опыте.
q = 1 – 0,01 = 0,99 – вероятность непоявления события А в одном опыте.
P1 = 0,99 – граница заданной вероятности появления А в n опытах.
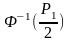аргумент
функции Лапласа для значения
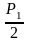(определяется по специальной таблицы).
Получаем:
=
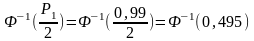0,1879.
=
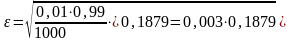0,005.
Ответ: от -0,005 до 0,005