2. Построение эпюр изгибающих моментов, продольных и поперечных сил в статически неопределимых рамах при силовом воздействии
Задача 2.1. Построить эпюры изгибающих моментов, продольных и поперечных сил в однопролетной одноэтажной раме (рис. 8).
Рис. 8. Расчетная схема рамы
Решение. Данная рама (рис. 8) является плоской статически неопределимой конструкцией. Расчет выполнен по программе Полюс. Результаты расчета рамы представлены на рис. 9 -13.
Рис. 9. Эпюра изгибающих моментов
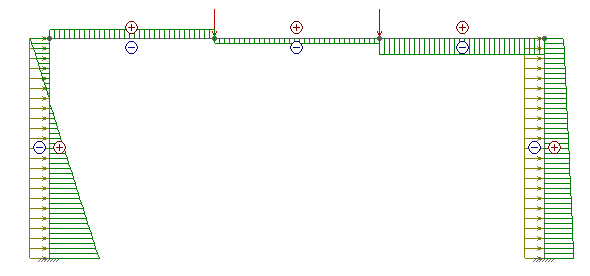
Рис. 10. Эпюра поперечных сил
Рис. 11. Эпюра продольных сил
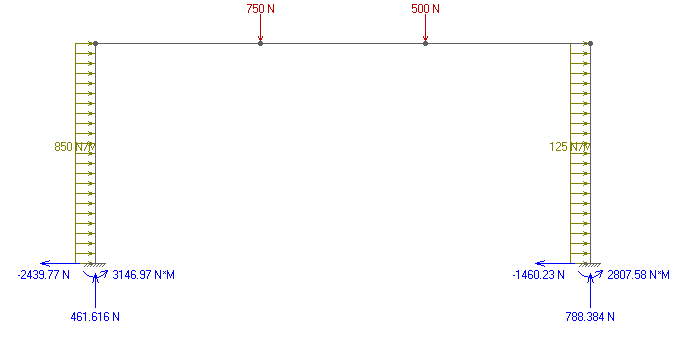
Рис. 12. Схема нагрузки и опорные реакции рамы
Рис.13. Схема перемещений узлов рамы
ОТЧЕТ ПО КОНСТРУКЦИИ (номера узлов и стержней по рис. 13):
Моменты
Стержень 1: M(3) = 187.879 M(1) = -3146.97
Стержень 3: M(4) = -2033.33 M(2) = -2807.58
Стержень 4: M(3) = -187.879 M(5) = -1196.97
Стержень 5: M(4) = 2033.33 M(6) = 331.818
Стержень 6: M(5) = 1196.97 M(6) = -331.818
Поперечные силы
Стержень 1: Q(3) = -960.227 Q(1) = 2439.77
Стержень 3: Q(4) = 960.227 Q(2) = 1460.23
Стержень 4: Q(3) = 461.616 Q(5) = 461.616
Стержень 5: Q(4) = -788.384 Q(6) = -788.384
Стержень 6: Q(5) = -288.384 Q(6) = -288.384
Продольные силы
Стержень 1: N(3) = -461.616 N(1) = -461.616
Стержень 3: N(4) = -788.384 N(2) = -788.384
Стержень 4: N(3) = -960.227 N(5) = -960.227
Стержень 5: N(4) = -960.227 N(6) = -960.227
Стержень 6: N(5) = -960.227 N(6) = -960.227
Перемещения
Узел 3: dx = 8218.18 dy = 0 da = 2136.36
Узел 4: dx = 8218.18 dy = 0 da = 881.818
Узел 5: dx = 8218.18 dy = -5177.27 da = 622.727
Узел 6: dx = 8218.18 dy = -2956.82 da = -1670.45
Узел 1: dx = 0 dy = 0 da = 0
Узел 2: dx = 0 dy = 0 da = 0
3. Построение эпюр изгибающих моментов, продольных и поперечных сил в статически неопределимых рамах при осадке опор
Задача 3.1. Построить эпюры изгибающих моментов, продольных и поперечных сил в рассмотренной выше (рис. 8) однопролетной одноэтажной раме, если фундамент левой опоры принудительно смещен вправо на 0,08 м и вверх на 0,05 м, а фундамент правой опоры принудительно смещен вниз на 0,1 м (рис. 14). Силовое воздействие не учитывать.
Рис.14. Схема рамы для расчета на осадку опор
Решение. По условию задачи необходимо выполнить расчет на кинематическое воздействие, вызванное принудительным смещением опор. Как и в случае силового воздействия, расчет статически неопределимых конструкций на осадку опор выполнен по программе Полюс, в которой реализован метод перемещений. Результаты расчета рамы представлены на рис. 15 - 19.
Рис. 15. Эпюра изгибающих моментов
Рис. 16. Эпюра поперечных сил
Рис. 17. Эпюра продольных сил
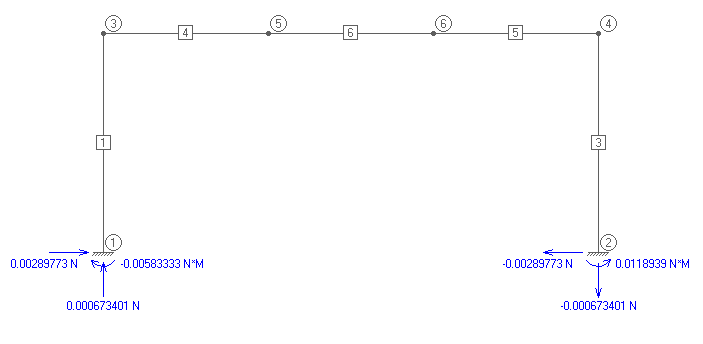
Рис. 18. Реакции опор при смещении фундаментов
Рис. 19. Перемещения узлов
ОТЧЕТ ПО КОНСТРУКЦИИ (номера стержней и узлов по рис. 19):
Моменты
Стержень 1: M(3) = 0.00575758 M(1) = 0.00583333
Стержень 3: M(4) = 0.00030303 M(2) = -0.0118939
Стержень 4: M(3) = -0.00575758 M(5) = 0.00373737
Стержень 5: M(4) = -0.00030303 M(6) = -0.00171717
Стержень 6: M(5) = -0.00373737 M(6) = 0.00171717
Поперечные силы
Стержень 1: Q(3) = -0.00289773 Q(1) = -0.00289773
Стержень 3: Q(4) = 0.00289773 Q(2) = 0.00289773
Стержень 4: Q(3) = 0.000673401 Q(5) = 0.000673401
Стержень 5: Q(4) = 0.000673401 Q(6) = 0.000673401
Стержень 6: Q(5) = 0.000673401 Q(6) = 0.000673401
Продольные силы
Стержень 1: N(3) = -0.000673401 N(1) = -0.000673401
Стержень 3: N(4) = 0.000673401 N(2) = 0.000673401
Стержень 4: N(3) = -0.00289773 N(5) = -0.00289773
Стержень 5: N(4) = -0.00289773 N(6) = -0.00289773
Стержень 6: N(5) = -0.00289773 N(6) = -0.00289773
Перемещения
Узел 3: dx = 0.0642424 dy = 0.05 da = -0.000151515
Узел 4: dx = 0.0642424 dy = -0.1 da = 0.0243939
Узел 5: dx = 0.0642424 dy = 0.0275758 da = 0.0140909
Узел 6: dx = 0.0642424 dy = -0.0284848 da = 0.0222727
Узел 1: dx = 0.08 dy = 0.05 da = 0
Узел 2: dx = 0 dy = -0.1 da = 0