ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «РОССИЙСКИЙ ЗАОЧНЫЙ ИНСТИТУТ ТЕКСТИЛЬНОЙ И ЛЕГКОЙ ПРОМЫШЛЕННОСТИ» Филиал ГОУ ВПО «РосЗИТЛП» в г. Омске Кафедра Общетехнических наук УТВЕРЖДАЮ Заведующий кафедрой _________________________ "______" ___________2008 г. ТЕПЛОМАССООБМЕННЫЕ ПРОЦЕССЫ И ОБОРУДОВАНИЕ Методические указания по решению типовых задач для студентов специальностей 220301,150406 Омск 2008

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОССИЙСКИЙ ЗАОЧНЫЙ ИНСТИТУТ ТЕКСТИЛЬНОЙ И ЛЕГКОЙ ПРОМЫШЛЕННОСТИ

Кафедра теплотехники

Теплотехника, тепломассообменные процессы и оборудование

Методические указания по решению типовых задач для студентов специальностей 170700, 210200

МОСКВА 2004

Составители: Б.С. Былинкин, С.А. Белов, И.А. Сафонова

Теплотехника, тепломассообменные процессы и оборудование: Метод, указания по решению типовых задач / Российск. заочн. ин-т текстил. и легк. пр-сти; Сост. Б.С.Былинкин и др. М., 2004, 31 с.

Предназначено для студентов специальностей:

170700 - «Машины и аппараты текстильной и легкой промышленности»

210200 -«Автоматизация технологических процессов и производств»

Содержание

2. Методические указания по решению типовых задач 5

2.1. Задачи по основам термодинамики 5

2.2 Задачи по тепловым аппаратам 18

П Р И Л О Ж Е Н И Е 23

1.Общие методические указания

Студенты заочники, руководствуясь программой курса и методическими указаниями, самостоятельно изучают теоретические основы курса и выполняют две письменные контрольные работы. Каждая из контрольных работ состоит из четырех задач.

К решению задач следует приступить после изучения соответствующего раздела курса. Перед выполнением контрольных работ рекомендуется ознакомиться с ходом решения аналогичных задач по учебной литературе,

Только сознательное (не «механическое») решение задач приносит пользу и помогает закреплению теоретических знаний Умение решать задачи, дать правильные ответы на вопросы для самопроверки является критерием усвоения учебного материала.

Исходные данные для каждой задачи выбираются из соответствующих таблиц по последней и предпоследней цифрам шифра, указанного в зачетной книжке. Работы, выполненные не по своему варианту, не рассматриваются.

При выполнении контрольных работ необходимо соблюдать следующие условия: а) выписывать полное условие задачи и исходные данные, б) асе расчеты прободать, используя только Международную систему единиц (СИ); в) решения всех задач должны содержать графические изображения процессов в термодинамических диаграммах и сопровождаться кратким анализом полученных результатов, г) в конце работы привести список использованной литературы и поставить свою подпись; д) для письменных замечаний рецензента оставить чистые поля в тетради и 1-2 страницы в конце работы.

2. Методические указания по решению типовых задач

2.1. Задачи по основам термодинамики

Задача 1

В резервуаре вместимостью V м³ газ находится под манометрическим (избыточным) давлением p_1м и температуре t₁. После медленного расходования из резервуара части газа манометрическое давление снизилось до p₂, а температура осталась прежней (t₁ = t₂).

Определить массу газа М₁ при его начальном состоянии и израсходованную массу газа ΔМ. Определить также при начальных параметрах плотность газа ρ₁, внутреннюю энергию U₁ и энтальпню J₁.

Атмосферное давление принять равным 1 бар= 10⁵ Па.

При решении задачи используются следующие термодинамические зависимости.

Уравнение состояния идеальных газов pV= MRT,

где р - абсолютное давление газа, Па;

V- объем газа, м³;

М - масса газа, кг;

Т - абсолютная температура газа, К;

R = 8314/μ- удельная газовая постоянная, Дж/кг∙град;

μ - молекулярная масса газа, кг/кмоль.

Внутренняя энергия газа U = М∙с_v,Т, Дж,

где с_v - удельная массовая теплоемкость газа при постоянном объеме, Дж/кг∙град.

Энтальпия газа J = Мс_р ·Т, Дж,

где с_p = с_v + R - удельная массовая теплоемкость газа при постоянном давлении.

Задача 2

Определить параметры газа в начальном и конечном состояниях, изменение внутренней энергии, теплоту, участвующую в заданном термодинамическом процессе, и работу, совершаемую газом, если заданы: масса газа М, начальные давление p₁, температура t₁ и температура t₂ газа в начале и конце процесса.

Для решения задачи необходимо использовать основные термодинамические закономерности:

Уравнение состояния идеальных газов

pV=MRT, (1)

где р - давление газа, Па;

V-объем газа, м³;

Т - абсолютная температура газа, К;

R = 8314/ μ - газовая постоянная, Дж/кг∙град

μ - молекулярная масса.

Количество подведенной к М кг газа (отведенной) теплоты определяется по уравнению

Q=c_{уд. проц.}(Т₂-Т₁), Дж (2)

где c_{уд. проц} - удельная теплоемкость газа в заданном процессе, Дж/кг∙град.

- Изменение внутренней энергии газа: U₂-U₁ = Mc_v(T₂ – T₁), Дж. (3)

- Механическая работа, совершаемая газом: L = p(V₂ – V₁), Дж. (4)

- Уравнение первого закона термодинамики; Q = (U₂ - U₁) + L. (5)

- Уравнения термодинамических процессов:

изохорный процесс (V = const)

p₁/T₁ = p₂/T₂, (6)

изобарный процесс (Р = const)

V₁/T₁ = V₂/T₂, (7)

адиабатный процесс (Q = 0)

p₁V₁^k = p₂V₂^k, (8)

где k = с_p/с_v - показатель адиабаты.

Зависимость между изобарной и изохорной теплоемкостям и даст формула Майера

c_p = c_v = + R. (9)

Пример 1. Определить параметры М кг газа в начальном и конечном состояниях, изменение внутренней энергии газа, отведенную теплоту и механическую работу при изменении температуры газа от t₁ до t₂ в изобарном процессе p₁ = const.

Решение:

1) При известных значениях t₁, t₂ и p₁ =р₂ определяем объем газа в начальном и конечном состояниях, используя уравнение состояния (1):

V₁ = MRT₁/p₁, м³, V₂ = MRT₂/p₂, м³,

здесь Т, К = t⁰С+273⁰ - абсолютная температура газа.

2) Определяем изменение внутренней энергии газа, используя формулу (3):

U₁ – U₂ = Mc_v(Т₂ – Т₁), Дж.

3) Теплота, отведенная от газа, вычисляется по формуле (2):

Q = Mc_p(Т₂ – Т₁), Дж.

4) Для определения механической работы воспользуемся формулой (4):

L = p(V₂ – V₁), Дж.

Пример 2. Определить параметры М кг газа в начальном и конечном состояниях, изменение внутренней энергии газа и работу расширения при изменении температуры газа от t₁ до t₂ в адиабатном процессе (т.е. без подвода или отвода теплоты, Q = 0).

Решение:

1). При известных значениях t₁, t₂ и p₁ определяем объем и давление газа в начальном и конечном состояниях, используя уравнения адиабаты (8) и состояния (1):

p₂ = p₁(T₂/T₁)^k/k-1, Па; V₁ = MRT₁/p₁, м³; V₂ = MRT₂/p₂, м³.

2) Определяем изменение внутренней энергии газа, используя формулу (3):

U₂ – U₁ = Mc_v(T₂ – T₁), Дж.

3) В соответствии с 1-м законом термодинамики (5) работа расширения газа в адиабатном процессе равна изменению внутренней энергии:

0 = - (U₂ - U₁) + L_ад, отсюда L_ад = U₁ - U₂…

Отметим, что идеальный (без трения) адиабатный процесс является изоэнтропным (S = const).

Задача 3

Газ (М кг) расширяется в цилиндре поршневого двигателя от начального давления p₁ и температуры t₁ ⁰С до конечного давления р₂;

Определить работу расширения газа для адиабатного политропного процессов, а также подводимую (отводимую) теплоту, изменение внутренней энергии и изменение энтропии.

При решении задачи используются следующие термодинамические зависимости:

Работа расширения газа при адиабатном процессе

L_ад = МR(T₁ – T₂)/(k – 1), где T₂ = T₁(P₂/P₁)^k-1/k;

k = c_p/c_v - показатель адиабаты,

c_p = c_v + R, Дж/кг∙град.

Работа расширения газа при политропном процессе

L_пол = МR(T₁ – T₂)/(n – 1), где T₂ = T₁(P₂/P₁)^n-1/n;

n = (с_пол - c_p)/( с_пол – c_v) – показатель политропы.

- Количество теплоты, подводимой или отводимой в процессе политропного расширения газа

Q_пол = Mcпол(Т₂ – Т₁), Дж

где с_пол =с_v[(n - k)/(n - 1)].

- Изменение внутренней энергии газа

ΔU = U₂ – U₁ = Mc_v(Т₂ – Т₁), Дж.

- Изменение энтропии газа

S_aд = const., ΔS_aд = S₁ - S₂ = 0

ΔS_пол = С_пол∙ln(T₂/T₁) Дж/град С_пол = с_v (n – k)/(n – 1)

Задача 4

Воздух с начальной температурой t₁ сжимается в поршневом компрессоре, где его давление повышается от p₁ до p₂. Сжатие осуществляется по изотерме, адиабате и политропе. Определить для каждого из этих процессов конечную температуру воздуха, отводимую теплоту в мощность компрессора, если его производительность G, кг/с.

Решение задачи.

Температура воздуха в конце процесса сжатия для адиабатного процесса Т₂ = Т₁(р₂/р₁^{)(k – 1)/k},

для политропного процесса Т₂ = Т₁(р₂/р₁^{)(n – 1)/n},

Отводимая теплота в Вт:

для изотермического процесса Q_из = -GRT∙ln p₂/p₁,

для адиабатного процесса Q_ад = 0

для политропного процесса Q_пол=G c_пол(Т₂ – Т₁)=G∙c_v[(n–k)/(n–1)](Т₂ – Т₁).

Мощность компрессора в Вт:

при изотермическом сжатии N_k = G∙l_{изотерм} = -G∙R∙Tlnp₂/p₁,

при политропном сжатии N_k = G∙l_полн = - G[n/(n – 1)]RT₁[(p₂/p₁)^(n-1)/n – 1],

при адиабатном сжатии

N_k = G∙l_ад = - G[k/(k – 1)]RT₁[(p₂/p₁)^(k-1)/k – 1].

Задача 5

Водяной дар с начальным давлением p₁ и степенью сухости х₁ поступает в пароперегреватель, где его температура повышается на Δt; после пароперегревателя пар изоэнтропно (по адиабате) расширяется в турбине до5давления p₂. Определить по i-s-диаграмме количество теплоты, подведенной к пару в пароперегревателе q_перегр, работу цикла Ренкина и степень сухости пара на выходе из турбины х₄. Определить также термический КПД цикла.

Одним из термодинамических рабочих тел, которое широко используется в технологических машинах и аппаратах отрасли, является водяной пар. Образование пара и нагрев его до заданной температуры осуществляется в паровом котле и пароперегревателе, которые по существу являются теплообменными аппаратами. Для анализа процесса парообразования и определения параметров пара обычно используется i-s диаграмма водяного пара (рис. 1)

Рис. 1. Изображение процесса парообразования в i-s диаграмме.

1 - линия при постоянном рабочем давлении пара, соответствующая процессу парообразования.

2 - кривая насыщения.

В котле вода сначала нагревается от температуры t₀ до температуры кипения t₁ = t_кип (отрезок 0-1), затем на отрезке 1-2 при постоянных значениях температуры t₁ = t_кип и рабочего давления p₁ происходит превращение воды в пар и далее перегрев пара до t = t₃ {отрезок 2-3).

Состав влажного насыщенного пара в области пол кривой насыщения 2 характеризуется степенью сухости влажного пара:

x = M_пар/М_вод + М_пар

Левая от критической точки ветвь кривой насыщения соответствует параметрам воды при температуре кипения и, следовательно, здесь х = 0, а правая ветвь - параметрам сухого насыщенного пара при х = 1.

Процессы нагрева воды, испарения воды в перегрева пара при p = const протекают в результате подвода соответствующих количеств теплоты: q_воды, q_{парообр} и q_{перегр.} Общее количество теплоты, требуемой для осуществления всего процесса 0-3, составляет:

q_∑ = q_воды + q_{парообр} + q_{перегр.} = Δi _воды +Δi_{парообр} + Δi _{перегр.} = i₃ – i₀, Дж∙кг

и может быть определено по i-s диаграмме.

Цикл Ренкина осуществляется в паросиловой установке (рис 2), где в качестве рабочего тела используется перегретый пар, который после расширения в турбине (Т) направляется в конденсатор (К) и полностью конденсируется в воду Вода с помощью насоса (Н) подается в котлоагрегат. Б паровом котле (ПК) при постоянном давлении осуществляется нагрев воды до температуры кипения и ее испарение. Полученный пар поступает в пароперегреватель (ПП), который обычно составляет одно целое с паровым котлом, перегревается там до заданной рабочей температуры и затем снова используется в турбине.

Рис. 2. Схема паросиловой установки.

Изображение идеального цикла Ренкина в i-s-диаграмме водяного пара показано на рис.3.

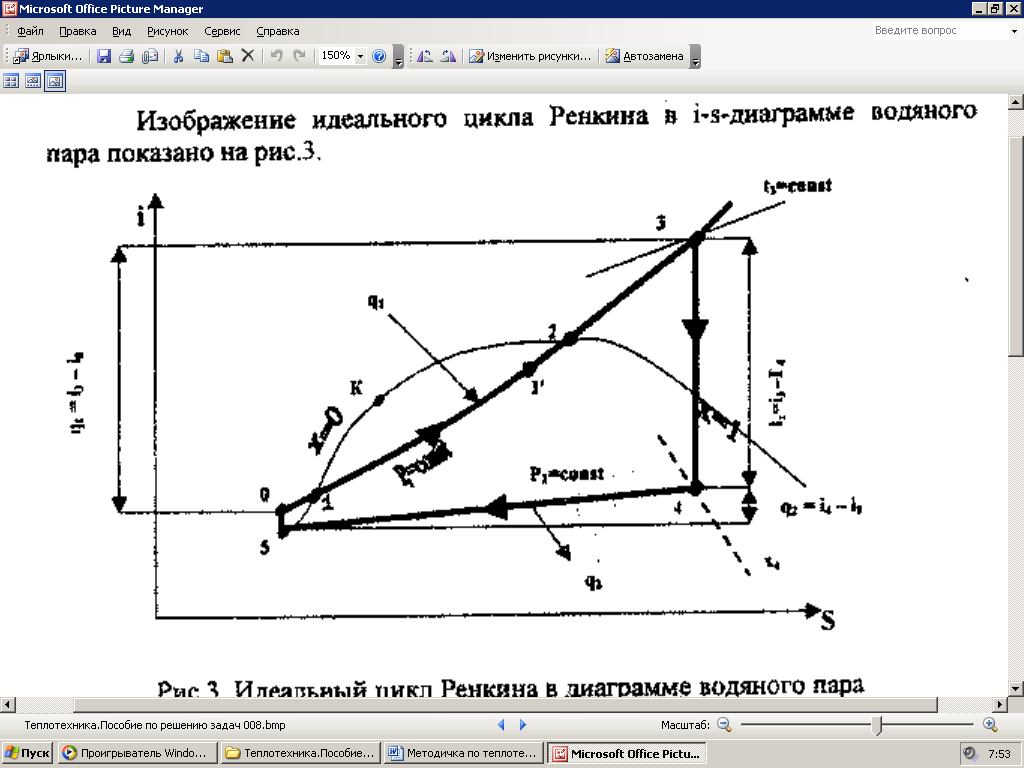
Рис. 3. Идеальный цикл Ренкина в диаграмме водяного пара.

В турбине перегретый пар адиабатно расширяется по линии 3-4. В соответствии с 1-м законом термодинамики для потока газа техническая работа, совершаемая паром в турбине, равна разности энтальпий пара до и после турбины: l_т = i₃ – i₄, Дж/кг

За турбиной в точке 4 пар обычно бывает влажным. По линии 4-5 пар конденсируется в конденсаторе при постоянном давлении р₂, следовательно, и постоянной температуре t₂, равной температуре насыщения при этом давлении. Выделяющееся при конденсации тепло q₂ отводится с охлаждаю шей водой. Из первого закона термодинамики для процессов при p=const следует:

q₁ = i₃-i₀ ~ i₃-i₅;

q₂ = i₄-i₅.

Термический КПД идеального цикла Ренкина, равный отношению полезной работы к затраченному теплу, определяется формулой:

η_t = l_ц/q₁~ l_турб/q₁~i₃ – i₄/ i₃ – i_5.

Величина энтальпии is соответствует температуре кипения воды при давлении р; и находится по таблицам.

Таким образом, методика решения данной задачи будет следующей :

- Температура пара иа входе в пароперегреватель (рис. 1)

t₁' = t_кип = t₁

- Температура пара перед турбиной t₃ = t₁ + Δt

- По i-s диаграмме определяем теплоту, подведенную к пару в пароперегревателе, q_{пороперегр} = i₃ – i₁^/, Дж/кг.

- определяем работу цикла Ренкина (см. рис. 3):

1_ц = 1_т = i₃ – i₄, Дж/кг и затраченную теплоту q₁ = i₃ – i₅, Дж/кг.

- Вычисляем термический КПД цикла η_t = i₃ – i₄/ i₃ – i_5.

- По i-s диаграмме определяется степень сухости пара х₄