2.1.2 Вынужденные колебания в контуре

Колебательного контура без потерь построить нельзя. В ре­альном контуре на преодоление активного сопротивления будет затрачиваться какая-то часть энергии. Поэтому при каждом пе­резаряде конденсатор будет получать все меньше и меньше энер­гии н амплитуда свободных колебаний будет уменьшаться.

Такие колебания, амплитуда которых с течением вре­мени уменьшается, называются затухающими колебаниями (рис. 2.2,6). Чем больше активное сопротивление катушки ин­дуктивности и потери энергии в конденсаторе, тем быстрее зату­хают колебания (рис. 2.2,в). Продолжительность колебаний в контуре определяется его добротностью.

Добротностью (или качеством) контура Q называется отно­шение реактивного (индуктивного x_L или емкостного х_с) сопро­тивления контура на частоте собственных колебаний f₀ к актив­ному сопротивлению R на той же частоте:

Величина, обратная добротности, называется затуханием контура:

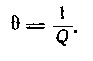
В контуре с высокой добротностью амплитуда колебаний убы­вает очень медленно. Современные колебательные контуры хоро­шего качества в диапазоне высоких частот имеют добротность Q= 100…200, а в диапазоне сверхвысоких частот — до многих тысяч.

В одиночном контуре даже с очень высокой добротностью ко­лебания затухают. Однако в ряде случаев требуется, чтобы коле­бания были незатухающими. Для этого от постороннего источ­ника необходимо периодически добавлять энергию в контур, ком­пенсируя имеющиеся в нем потери.

Колебания, возникающие в контуре под непрерывным воздей­ствием внешнего источника, называются вынужденными колеба­ниями. Для получения вынужденных колебаний источник пере­менной ЭДС может подключаться к элементам контура последо­вательно или параллельно (рис. 2.4). При этом частота вынуж­денных колебаний определяется частотой постороннего источ­ника и может отличаться от собственной частоты контура.

2.1.3 Резонанс в колебательном контуре

При совпадении частот вынужденных колебаний, с собствен­ной частотой контура наступает явление резонанса. При резо­нансе ток в контуре достигает наибольшей величины. Частота ко­лебаний ЭДС внешнего источника, при котором наступает явле­ние резонанса, называется резонансной частотой и обозначается f_рез.

Явление резонанса можно получить изменением частоты ЭДС внешнего источника при неизменной частоте собственных колеба­ний контура или настройкой контура, т. е. изменением частоты собственных колебаний контура при неизменной частоте внешнего источника. В последнем случае для получения резонанса изме­няют либо индуктивность, либо емкость контура, или то и другое вместе до совпадения собственной частоты контура с частотой внешнего источника.

На рис. 2.3 показано, как изменяется величина тока I в кон­туре с изменением его частоты. По мере приближения к резонансу ток в контуре увеличивается. В момент резонанса он достигает наибольшего значения, по мере удаления от резонанса — умень­шается.

Графическая зависимость тока в контуре от частоты вблизи резонанса называется резонансной кривой. Из рис. 2.3, на кото­ром изображены резонансные кривые двух контуров различной добротности, можно сделать заключение о том, что чем больше добротность контура, тем более острый вид имеет его резонанс­ная кривая, тем больше разница между амплитудой тока резо­нансной частоты и другими частотами, воздействующими на ко­лебательный контур.

Способность контура выделять из всех подводимых колебаний только те колебания, частота которых близка к резонансной, на­зывается избирательностью контура. Полоса частот, в пределах которой величина тока в контуре составляет не менее 0,707 от тока при резонансе, называется полосой пропускания контура и обозначается 2F. Собственная частота контура f₀, полоса про­пускания 2F й добротность контура Q связаны соотношением

Чем выше добротность контура, тем меньше его полоса про­пускания: Q₂>Q₁; 2F₂<2F_i.

В зависимости от способа подключения источника внешней ЭДС в контуре различают два вида резонанса: резонанс напря­жении н резонанс тока.

Резонанс напряжений

Резонанс напряжений возникает при последовательном соеди­нении источника внешней ЭДС с индуктивностью и емкостью кон­тура (рис. 2.4,а), когда частота источника равна частоте собственных колебаний контура f_ист=f₀. В этом случае реактивные со­противления катушки индуктивности и емкости равны по величине x_L = x_C.

Входное (общее) сопротивление контура мало и равно его активному сопротивлению Zpeз=R, так как противоположные по знаку сопротивления x_L и х_С компенсируют друг друга; сопротив­ление контура имеет активный характер:

Величина тока при резонансе вследствие малого сопротивле­ния контура достигает максимального значения:

Этот ток, протекая по последовательно соединенным элемен­там контура, создает на катушке индуктивности и конденсаторе равные по величине падения напряжения U_L = U_С. Напряжения н Uc могут значительно превышать ЭДС источника.

Это значит, что при резонансе напряжений можно получить выигрыш в напряжении, который определяется качеством кон­тура Q:

Чем выше качество контура Q, тем больше напряжение на эле­ментах контура будет превышать ЭДС источника тока.

Резонанс токов

Резонанс токов возникает при параллельном соединении ис­точника внешней ЭДС с индуктивностью и емкостью контура (рис. 2.4,б), когда частота источника равна частоте собственных колебаний контура:

В этом случае реактивные сопротивления катушки индуктивно­сти и емкости контура также равны: Х_L — Х_С.

Ток в отдельных ветвях контура (в противоположных па знаку сопротивлениях) имеет противоположные направления, образуя единый круговой (контурный) ток. Поскольку реактив­ные сопротивления компенсируют друг друга, то контурный ток /к достигает большой величины.

Этот контурный ток, протекая по катушке индуктивности L и емкости С, создает на них значительные падения напряжения, ко­торые как бы уравновешивают ЭДС источника: E=U_L=U_C. Поэтому ток в общей ветви при резонансе токов мал, I_общ мало.

Малая величина тока в общей ветви (до разветвления) свиде­тельствует о том, что резонансное сопротивление параллельное контура, т. е. его входное сопротивление, велико:

Сопротивление контура имеет активный характер и зависит от качества контура Q. Чем выше качество контура, тем больше его резонансное сопротивление.

Отношение величины контурного тока I_к к току в общей вет­ви I_общ равно качеству контура:

Таким образом, при резонансе токов создается выигрыш в токе, который определяется качеством контура Q. Чем выше ка­чество контура, тем больше выигрыш в токе.