
- •Глава I Пространственно-временная обработка радиолокационной информации
- •1.2. Пространственно-временная обработка
- •1.3. Пространственно-временная обработка радиолокационной информации
- •Глава II Первичная обработка радиолокационной информации
- •2.1. Обнаружение радиолокационных сигналов
- •2.1.3. Оптимальное обнаружение полностью известного сигнала
- •2.1.6. Принципы фильтровой и корреляционно—фильтровой обработки сигналов
- •2.1.7. Принципы оптимальной обработки некогерентных сигналов
- •2.1.8. Принципы обработки широкополосных сигналов
- •2.1.9. Ранговые обнаружители
- •2.1.10. Стабилизация уровня ложных тревог
- •2.2. Измерение параметров радиолокационных сигналов
- •2.2. 6. Методы измерения угловых координат
- •2.2.7. Многоканальные (моноимпулъсные) методы измерения угловых координат
- •2.2.8. Методы измерения скорости
- •2.2.9. Методы определения местоположения объектов
- •2.3.4. Разрешаемый объем
- •2.4. Распознавание воздушных объектов
- •2.5. Обработка сигналов в условиях воздействия пассивных помех и отражений от «местных предметов».
- •2.5.3. Когерентность сигналов
- •2.5.5. Радиолокаторы с внешней когерентностью
- •2.5.7. Селекция сигналов движущихся целей
- •2.5.8. Особенности систем сдц
- •2.5.8.1. Понятие слепого направления.
- •2.5.8.2, «Слепые» фазы.
- •2.5.9. Подавитель на промежуточной частоте
- •2.5.10. Череспериодное вычитание
- •2.5.11. «Слепые» скорости воздушных объектов
- •2.5.12. Применение систем сдц для компенсации сигналов
- •2.5.13. Цифровая система селекции движущихся целей
- •2,5.14. Основные характеристики систем сдц
- •2.5.15. Некоторые методы скоростной селекции
- •2.6. Обработка сигналов в условиях воздействия импульсных помех
- •2.6.1. Обработка сигналов в условиях воздействия несинхронных импульсных помех
- •2.6.2. Обработка сигнала на фоне шума и сигнальных импульсных помех
- •2.6.2.1. Понятие о динамическом диапазоне сигналов и помех и необходимости их нормирования
- •2.6.2.2. Нормирование уровня длинных импульсных помех с помощью схемы шоу
- •2.6.2.3. Нормирование уровня длинных импульсных помех с помощью схемы рос
- •2.6.2.4. Нормирование уровня коротких и длинных помех с помощью схемы шоу-рос
- •2.7. Системы подавления сигналов боковых лепестков диаграмм направленности антенн
- •2.7.1. Классификация систем подавления сигналов боковых лепестков
- •2.8. Активные маскирующие помехи и принципы защиты от них
- •2.8.2. Искусственные маскирующие активные помехи, особенности воздействия и способы создания
- •3.3, Алгоритм вторичной обработки
- •Глава IV третичная обработка информации
- •4.1. Принципы, способы и классификация третичной обработки радиолокационной информации
- •5.3. Кодирование запросных и ответных сигналов
- •5.3.1. Методы кодирования запросных и ответных сигналов
- •5.3.2. Структура запросных сигналов
- •5.3.3. Структура ответных сигналов
- •5.3.3.1. Ответный сигнал режима увд
- •6.4.3.2 Ответный сигнал режима rbs
- •5.4. Дешифрация ответной информации
- •5.4.1. Дешифрация сигналов в режиме увд
- •5.4.2. Дешифратор режима международного диапазона
- •5.5. Дискретно-адресная система вторичной радиолокации
- •5.6.. Моноимпульсный метод измерения
- •Содержание
- •Глава I Пространственно - временная обработка радиолокационной информации
- •Глава II Первичная обработка радиолокационной информации
- •Глава III Вторичная обработка радиолокационной информации
- •Глава IV Третичная обработка информации
- •Глава V Обработка сигналов средств вторичной радиолокации
2.1.7. Принципы оптимальной обработки некогерентных сигналов
Некогерентными называются сигналы, фазовую структуру которых нельзя считать закономерной. Такого вида сигналы часто встречаются в обзорных радиолокаторах. В силу случайности начальных фаз, когерентное накопление возможно лишь в пределах каждого из одиночных радиоимпульсов. Накопление же от импульса к импульсу может быть только последовательным - некогерентным.
Частное отношение правдоподобия представляет собой произведение двух степенных функций: степенной функции полного корреляционного интеграла Z и степенной функции полной энергии Э пачки
![]() ,
,
![]() ,
,
где
![]() - модульное значение частного
корреляционного интеграла, вычислен-
- модульное значение частного
корреляционного интеграла, вычислен-
ное
для случая, когда ожидаемым сигналом
является г-й радиоимпульс;
![]() -
амплитудные множители, тождественно
равные единице при не-
-
амплитудные множители, тождественно
равные единице при не-
флюктуирующей пачке.
Для некогерентных пачек отношение правдоподобия представляет собой произведение отношений правдоподобия для одиночных радиоимпульсов соответствующего вида, т.е. со случайной начальной фазой или случайными амплитудой и начальной фазой


Сравнение значений отношений правдоподобия / с порогом /0 может быть заменено сравнением со своими порогами значений In/. Для рассматриваемых случаев
![]() , (28)
, (28)
![]() .
(29)
.
(29)
Оптимальные обнаружители, построенные в соответствии с соотношениями (28) и (29), вычисляют модульные значения корреляционных интегралов и суммируют в общем случае нелинейные функции этих модульных значений.
Для
нефлюктуирующих некогерентных пачек
суммирование логарифмов
![]() заменяется суммированием линейных или
квадратичных функций величины
,
а именно, квадратичных, если амплитуды
радиоимпульсов малы по сравнению
с уровнем шума,
заменяется суммированием линейных или
квадратичных функций величины
,
а именно, квадратичных, если амплитуды
радиоимпульсов малы по сравнению
с уровнем шума,
![]()
и линейных, если они велики
![]() .
.
Обычно
комплексные амплитуды всех ожидаемых
импульсов пачки соответствуют
одному и тому же закону модуляции. Они
различаются только: 1) моментами прихода
импульсов
![]() ,
зависящими
от моментов зондирования и дальности,
и 2) неслучайными множителями Si
зависящими
от формы огибающей пачки и угловой
координаты. Поэтому все значения
,
зависящими
от моментов зондирования и дальности,
и 2) неслучайными множителями Si
зависящими
от формы огибающей пачки и угловой
координаты. Поэтому все значения
![]()
пропорциональны
амплитудам некоторых однотипно
получаемых видеоимпульсов
![]() .
Последние могут быть сняты с выхода
единственного канала приема
последовательно во времени. Достаточно,
чтобы этот канал содержал схему
.
Последние могут быть сняты с выхода
единственного канала приема
последовательно во времени. Достаточно,
чтобы этот канал содержал схему
когерентной обработки для ожидаемого сигнала (оптимальный фильтр) и линейный детектор. Чтобы получить квадраты амплитуд Z\{ линейный детектор заменяется квадратичным. Рассмотренный канал приема не учитывает форму огибающей пачки радиоимпульсов и не обеспечивает последетекторное суммирование. Указанные операции реализуются в следующей схеме оптимальной обработки (рис. 2.13).
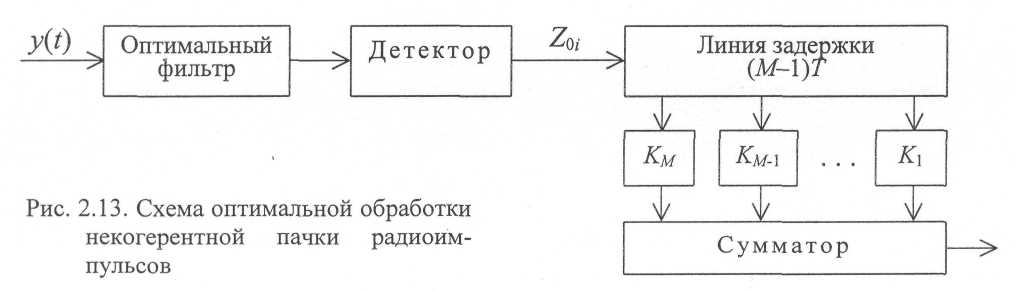
В
случае слабой нефлюктуирующей пачки,
когда оптимален квадратичный
детектор, последовательное суммирование
импульсов производится с весовыми
коэффициентами
![]() .
В
случае нефлюктуирующей пачки импульсов
большой амплитуды оптимален линейный
детектор и последовательное суммирование
производится с весовыми коэффициентами
Ki
=Si
. В
случае флюктуирующей
пачки оптимален квадратичный детектор
и последовательное суммирование
производится с весовыми коэффициентами:
.
В
случае нефлюктуирующей пачки импульсов
большой амплитуды оптимален линейный
детектор и последовательное суммирование
производится с весовыми коэффициентами
Ki
=Si
. В
случае флюктуирующей
пачки оптимален квадратичный детектор
и последовательное суммирование
производится с весовыми коэффициентами:
 ,
где
,
где
![]() - отношение сигнал-помеха для
- отношение сигнал-помеха для
импульса с весовым множителем единица, средняя энергия которого равна Эо.
При обработке пачки отраженного сигнала определенные трудности возникают при осуществлении задержки, измеряемой длительностью пачки. В этом случае может быть использована одна линия задержки на период посылки, но за счет положительной обратной связи с выхода на вход ее превращают в рециркулятор на видеочастоте (рис. 2.9).
Широкое распространение находят схемы цифрового накопления или, иначе, схемы счета числа импульсов, превышающих порог. С учетом пропуска
отдельных
импульсов из-за флюктуации или наложения
противофазных шумов решение
о наличии цели принимается, если налицо
k
и
более импульсов из т
возможных
(критерий к/т).
Для
каждого т
существует
оптимальное значение
![]() .
Потери цифрового суммирования, по
сравнению с квадратичным, не
превышают ЗдБ.
.
Потери цифрового суммирования, по
сравнению с квадратичным, не
превышают ЗдБ.
