2.2.7. Многоканальные (моноимпулъсные) методы измерения угловых координат

Получившие широкое распространение одноканальные методы пеленга­ции, отличаясь сравнительной простотой, не всегда обеспечивают достаточную точность измерения. Основной причиной являются искажения огибающей пач­ки отраженных импульсов за счет флюктуации вторичного излучения. Этот не­достаток одноканальных методов устраняется при переходе к многоканальным. При этом для измерения каждой угловой координаты используется несколько самостоятельных приемных каналов, чаще всего два.

Многоканальные методы и системы пеленгации делят на амплитудные и фазовые. В них используются зависимости амплитуд или фаз принимаемых ко­лебаний от направления прихода радиоволн, неодинаковые для различных ка­налов приема.

Рис. 2. 56. Блок-схема двухканального амплитудного пеленгатора

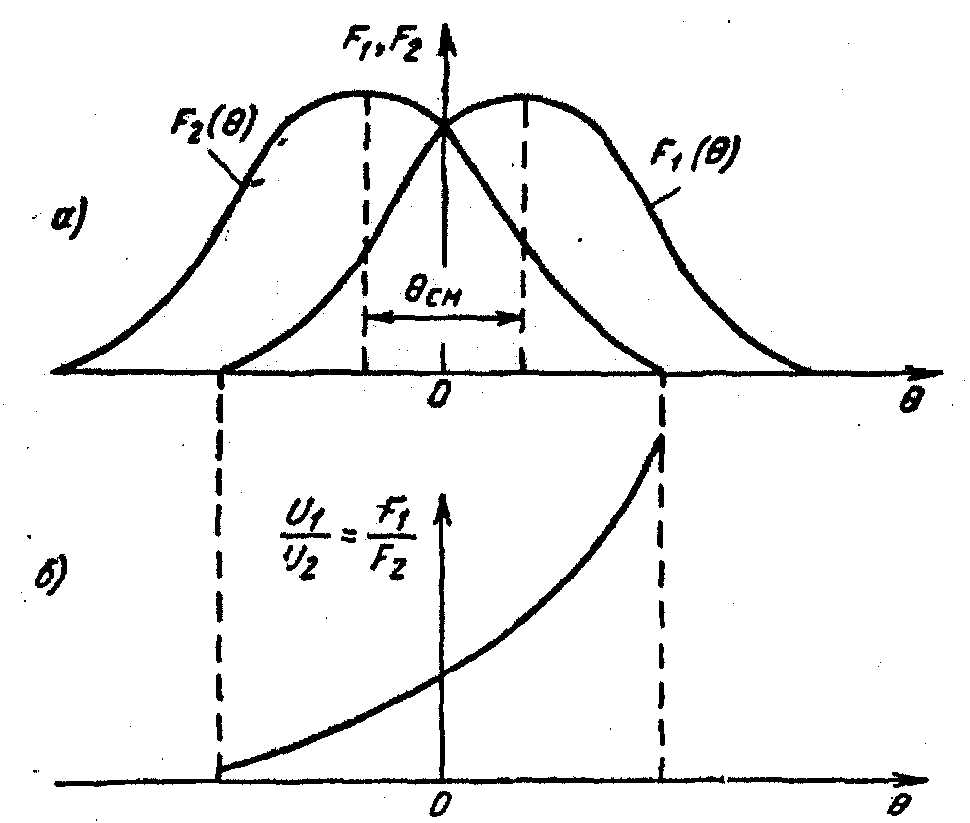
Рис. 2.57. Диаграммы направленности (а) и зависимость отношения амплитуд от углового положения цели (б)

Рис. 2.58. Пеленгатор с логарифмическими усилителями (а) и пеленгационная характеристика (б)

На рис. 2.56 представлена простейшая двухканальная амплитудная сис­тема пеленгации. На приемные каналы поступают колебания от сдвинутых из фокуса зеркала антенны облучателей. Различным каналам соответствуют сме­щенные на некоторый угол 0см диаграммы направленности. Продетектированные импульсы с выхода приемников первого и второго каналов поступают на схему сравнения амплитуд, которая определяет их отношение. График зависи­мости отношения амплитуд от положения цели относительно оси антенной системы для смещенных диаграмм направленности каналов F₁(θ) и F₂(θ) показан на рис. 2.57. В соответствии с этим графиком по величине отно­шения амплитуд может быть найдено смещение цели θ относительно равносигнального направления (U₁/U₂=l). Угловая координата цели θ_Ц = θ + θ₀ опреде­ляется при этом алгебраической суммой измеренной величины θ и угла пово­рота антенны θ₀, который вводится в счетно-решающее устройство.

В отличие от одноканального амплитудный двухканальный метод позво­ляет измерять угловую координату по одному принятому импульсу и вместе с другими многоканальными методами (применительно к случаю импульсного зондирования пространства) относится к классу моноимпульсных методов пе­ленгации. Наиболее важным их достоинством является нечувствительность к флюктуациям амплитуд отраженного сигнала, что для схемы рис.2.56 непосредственно вытекает из принципа их сравнения в один и тот же момент вре­мени.

Задача сравнения амплитуд облегчается, если в приемнике используются усилители с логарифмическими амплитудными характеристиками (рис. 2.58, а). Схема сравнения сводится в этом случае к вычитающему устройству, по­скольку

.

Зависимость полученной величины от угла рассогласования θ (пеленгационная характеристика) показана на рис. 2.58, б. Другой способ сравнения ам­плитуд связан с использованием автоматической регулировки усиления (АРУ) колебаний промежуточной частоты обоих каналов (рис. 2.59). Если в качестве регулирующего используется одно и то же напряжение, а усилители идентич­ны, то амплитуды их выходных напряжений U_вых1=kU₁ и U_вых2=kU₂ пропорцио­нальны амплитудам входных, причем коэффициент пропорциональности (ко­эффициент усиления k) в обоих случаях одинаков. Пусть регулирующее этот коэффициент напряжение выбирается из условия практического постоянства амплитуды выходного напряжения второго канала U_вых2=c. В этом случае к = c/U₂, а амплитуда выходного напряжения первого канала U_вых1 = c(U₁/U₂) ока­зывается пропорциональной отношению амплитуд напряжений на входе перво­го и второго каналов.

Рис. 2.59. Пояснение способа сравнения амплитуд с использованием автоматической регулировки усиления

С учетом боковых лепестков диаграмм направленности зависимость U₁/U₂ = f(θ) или lg(U₁/U₂) = φ(θ) не всегда является гладкой и монотонной, ка­кой она показана на рис. 2.57. Немонотонность этой зависимости может вести к неоднозначности измерений при U₁/U₂ » 1 или U₁/U₂ « 1. Последняя несуще­ственна, если измеряются лишь малые отклонения равносигнального направ­ления от направления на цель (U₁/U₂ ≈ 1) или если для измерения используются несколько (более двух) приемных каналов.

На рис. 2.60 показана моноимпульсная амплитудная система с рядом парциальных каналов, перекрывающих сектор обзора по одной из угловых коорди­нат, например по углу места. Сама антенная система может при этом поворачи­ваться, например, по другой координате, осуществляя обзор (сканирование). Сканирование может производиться также электрическим путем без перемеще­ния антенной системы. Продетектированные напряжения приемных парциаль­ных каналов поступают на схему сравнения амплитуд. В этой схеме направле­ние на цель грубо определяется по номеру парциального канала, выходной сиг­нал которого имеет наибольшую амплитуду. Для уточнения и устранения неод­нозначности отсчета могут использоваться значения амплитуд соседних каналов.

Рис. 2.60. Принцип пеленгации методом парциальных диаграмм

Решение об измеренной координате может выдаваться в результате ана­логовой или цифровой обработки. В последнем случае значения амплитуд на­пряжений на выходе канальных приемников квантуются и переводятся в циф­ровую форму.

Перейдем к рассмотрению фазовых методов многоканальной пеленгации. На рис. 2.61 показана двухканальная фазовая система пеленгации, в которой ис­пользуется разнос приемных антенн на величину d, называемую базой. Прини­маемые колебания приходят в антенны со сдвигом фаз

где λ —длина волны колебаний передатчика, θ — угол между направле­нием прихода радиоволн и нормалью к базе.

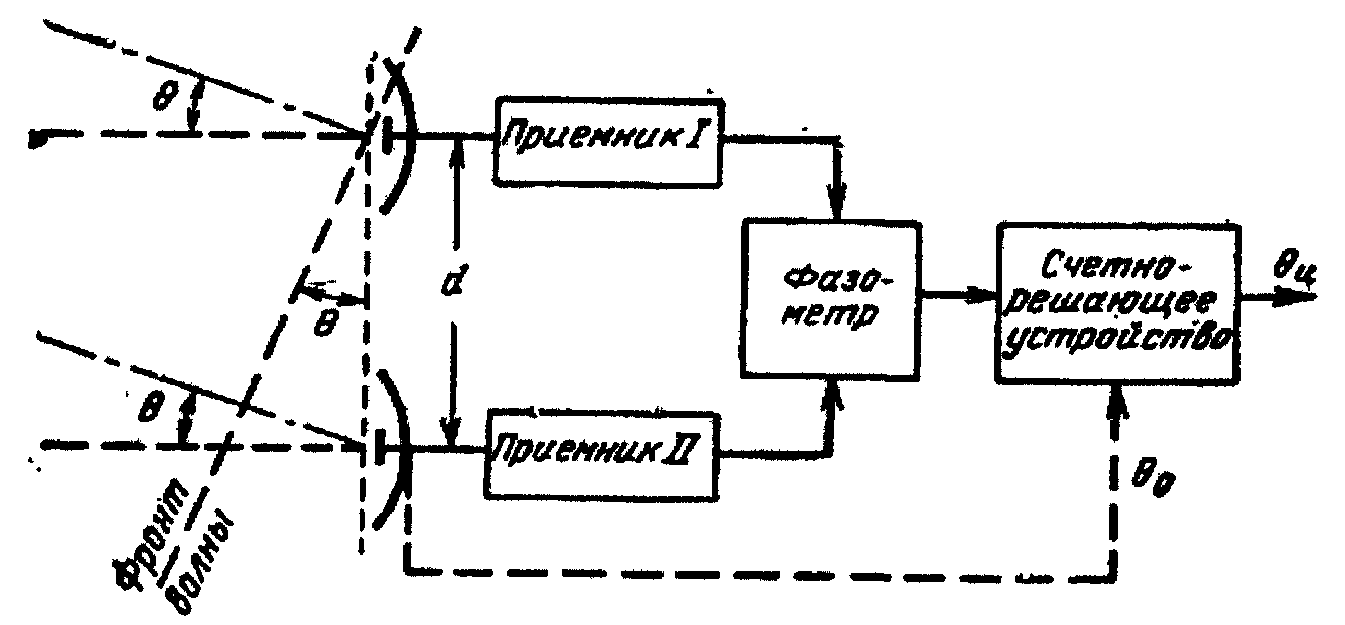
Рис. 2.61. Блок-схема двухканального фазового пеленгатора

Далее колебания усиливаются приемниками и поступают на фазометр, который измеряет разность фаз φ₁—φ₂, зависящую от угловой координаты це­ли. Фазометр может быть проградуирован в единицах углового отклонения це­ли от нормали к базе θ, так что θ_ц – θ₀ + θ.

Как и амплитудная, фазовая система мно­гоканальной пеленгации позволяет определять угловое положение цели по одному принятому импульсу и относится к классу моноимпульсных. Она практически нечувствительна к флюктуациям отраженного сигнала.

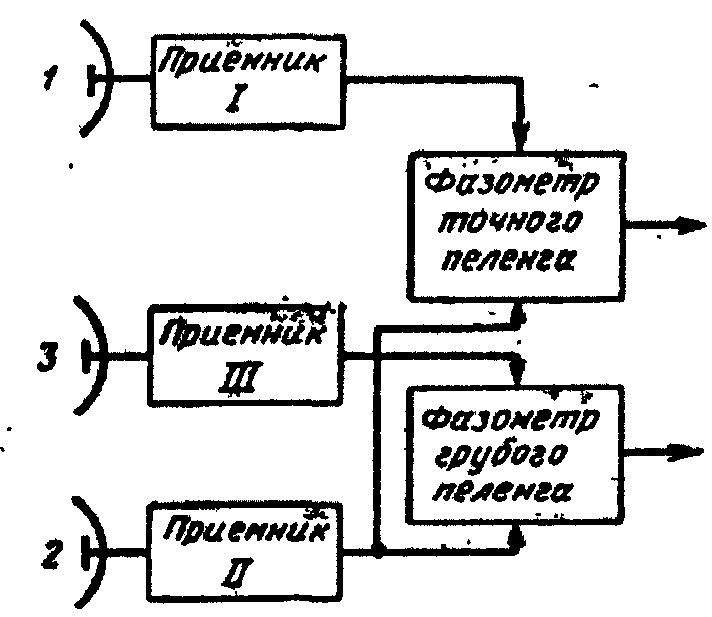
Рис. 2.62. Устранение неоднознач­ности пеленга путем применения третьего канала

Поскольку разность фаз φ₁—φ₂ определя­ется с точностью до слагаемого, кратного 2π, возможна неоднозначность отсчета. Неоднозначность устраняется за счет высокой направленности антенн, когда для углов θ в пределах главного лепестка диаграммы направленности разность фаз φ₁—φ₂ не превышает 2π. Для расширения сектора однозначного отсчета можно ввести третий антенно-приемный канал (рис. 5.66) с уменьшенной базой между ним и одним из двух других каналов. По разности фаз φ₁—φ₂ сигналов, принятых антеннами 1 и 2, угловая координата цели определяется с высокой точностью, но неоднозначно. Измерив разность фаз φ₁—φ₂ сигналов, принятых антенна­ми 2 и 3, можно устранить неоднозначность отсчета, подобно тому, как неодно­значность точного отсчета времени с помощью минутной стрелки устраняется отсчетом с помощью часовой. И в том, и в другом случае мы имеем дело с уст­ранением неоднозначности за счет многошкальных измерений.

Использование суммарно-разностных методов измерения в моноимпульсных системах

Широкое применение в моноимпульсных системах находит суммарно-разностная обработка колебаний, принимаемых различными каналами. При та­кой обработке образуются сумма и разность двух колебаний. Чтобы облегчить требования к идентичности и динамическому диапазону каналов приема, раз­дельную обработку принимаемых колебаний заканчивают схемой образования разности в самом начале приемного тракта, на высокой частоте.

Для получения суммарного и разностного колебаний обычно использу­ются высокочастотные мостовые схемы на волноводах, либо на коаксиальных линиях.

На рис.2.63 показана схема кольцевого суммарно-разностного волноводного моста. Принятые сигналы подводятся к отводам моста 1 и 2. С отвода «с» снимается суммарное колебание, а с отвода «р» — разностное. Фаза разностно­го колебания определяется фазой того из пары входных сигналов, амплитуда которого больше. Вместо кольцевого моста часто используется двойной волноводный тройник.

Суммарно-разностная обработка применяется в моноимпульсных систе­мах, основанных как на сравнении амплитуд, так и на сравнении фаз прини­маемых колебаний.

На рис. 2.64 показано подключение суммарно-разностного волноводного моста к антенной системе амплитудной моноимпульсной РЛС, измеряющей од­ну угловую координату. В этой РЛС имеются два угловых канала с неодинаковыми характеристиками направленности при общем фазовом центре. Рис. 2.65 поясняет образование суммарной и разностной диаграмм.

Колебания передатчика приходят к облучателям антенны синфазными, образуя суммарную диаграмму направленности антенны на излучение F_c(θ) = F₁(θ) + F₂(θ). Суммарная диаграмма на прием аналогична суммарной диаграмме на излучение. Зависимость раз­ностного напряжения от углового отклонения цели оп­ределяется разностной диаграммой направленности F_p(θ) = F₂(θ)-F₁(θ). При этом в соответствии со знаком углового отклонения цеди от оси системы фазы колебаний суммарного и разно­стного каналов оказываются либо одинаковыми, либо отличающимися на π, что характеризует сторону углового рассогласования. Амплитуда разностного ко­лебания при малых угловых рассогласованиях пропорциональна величине уг­лового отклонения цели.

Рис. 2.63. Схема кольцевого суммарно-разностного волно­водного моста

Таким образом, разностная диаграмма направленности обладает дискриминаторными свойствами по углу и позволяет определять величину и знак уг­лового рассогласования. Для определения величины и знака рассогласования служит фазовый детектор, в котором в качестве опорного напряжения исполь­зуется суммарный сигнал. На выходе фазового детектора получаются видеоим­пульсы, полярность которых зависит от знака рассогласования. После расширения и усиления эти импульсы используются для привода исполнительного устройства следящей системы, управляющей положением антенной системы.

Для измерения угловых координат амплитудным моноимпульсным мето­дом в двух плоскостях используются две аналогичные системы с общим сум­марным каналом.

В фазовых моноимпульсных измерителях имеются угловые каналы с оди­наковыми характеристиками направленности, но разнесенными фазовыми цен­трами (см. рис. 2.61). Для измерения разности фаз мгновенных значений двух колебаний u₁(t), u₂(t) также широко используется суммарно-разностная обра­ботка. В фазометрах суммарно-разностного типа образуются сумма и разность входных колебаний, амплитуды которых одинаковы:

.

Рис. 2.64. Подключение суммарно-разностного волноводного моста к антенне амплитудной моноимпульсной РЛС

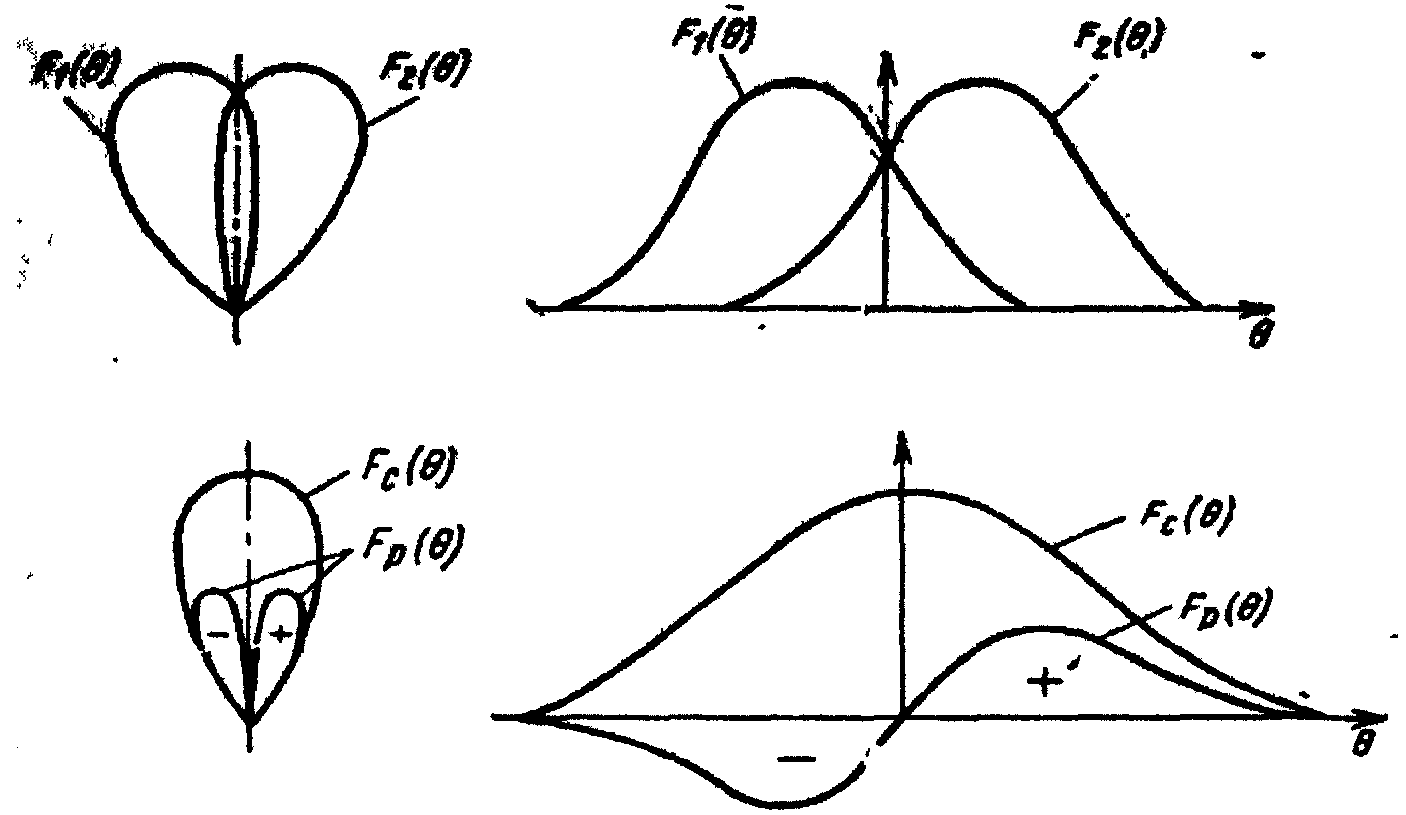
Рис. 2.65. Пояснение образования суммарной и разностной диаграмм на­правленности антенной системы амплитудной моноимпульсной РЛС

Для суммирования и вычитания можно использовать, например, плечи Н и Е двойного волноводного тройника, если входные сигналы подавать в его бо­ковые плечи. Для этой же цели пригоден волноводно-щелевой мост. Суммар­ный и разностный сигналы усиливаются разными каналами, но требования к их идентичности ниже, чем при прямом измерении разности фаз.

Отношение амплитуд разностного и суммарного сигналов, которые обо­значим здесь U_- и U₊, зависит только от разности фаз исходных сигналов

,

что иллюстрируется на градуировочной кривой (рис. 2.66.). Как видно из ри­сунка, по отношению амплитуд U_- / U₊ можно определить разность фаз φ₁—φ₂. Однако интервал однозначного измерения разности фаз составляет в этом слу­чае только π радиан.

Рис. 2.66. Градуировочная кривая фазометра со схемой деления на видеочастоте

Рис. 2.67. Градуировочная кривая фазометра со схемой деления на радиочастоте

Интервал однозначного измерения расширяется, если использовать от­ношение мгновенных значений разностного и суммарного напряжений, пропус­тив предварительно одно из них через девяностоградусный фазовращатель. По­скольку сравниваемые колебания после этой операции приводятся к одной фа­зе, получим

,

где индекс _┴ указывает на операцию сдвига фазы на 90°. Из градуировочной кривой (рис. 2.67) следует, что интервал однозначного измерения расширен до 2π.

Отношение амплитуд или же мгновенных значений колебаний может быть визуально измерено с помощью осциллографа, на вертикальные и гори­зонтальные пластины которого подают продетектированные или недетектированные соответствующие напряжения.

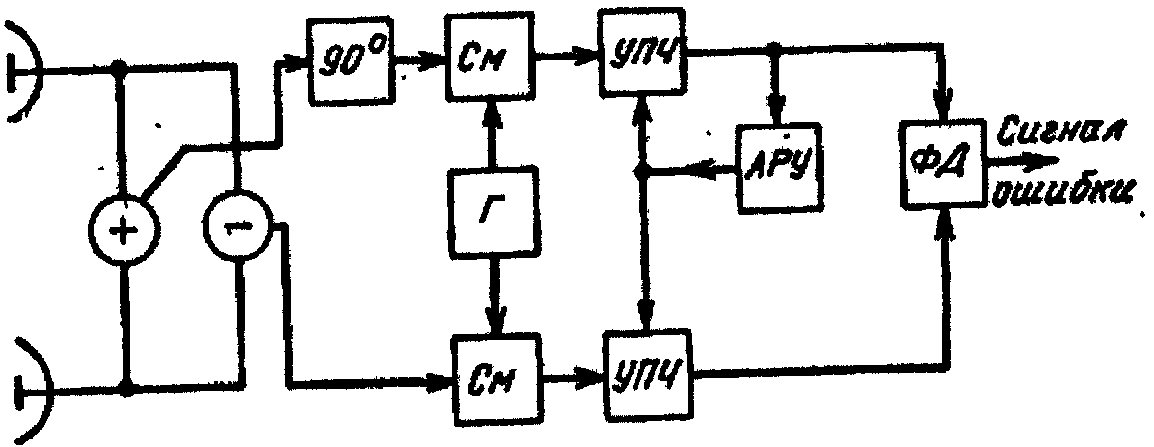
Рис. 2.68. Блок-схема фазового пеленгатора, использующего для

получения сигнала ошибки углового рассогласования схемы АРУ

и фазового детектора

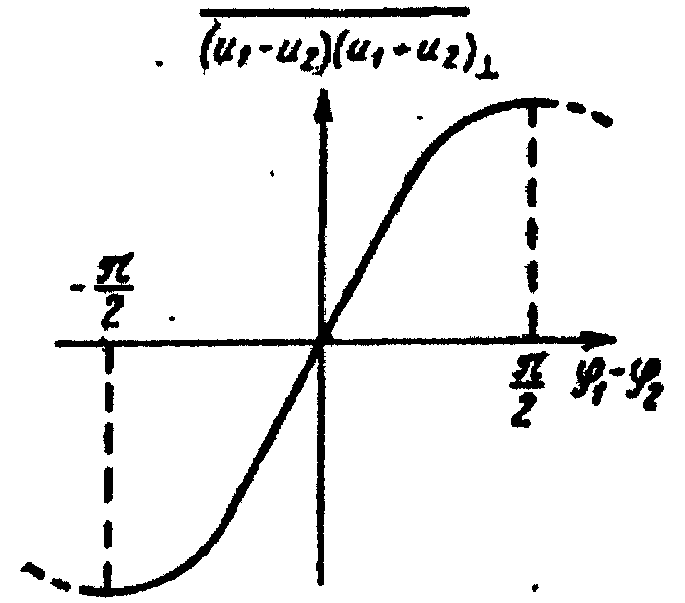
Рис. 2.69. Градуировочная кривая фазомет­ра со схемой умножения на радиочастоте (без делящей АРУ)

Изображение на экране имеет вид черты, наклон которой определяется величиной отношения напряжений, а значит, и величиной измеряемой разно­сти фаз.

Автоматизированное деление амплитуд разностного и суммарного сиг­налов можно осуществить за счет использования соответствующих усилителей с быстрой автоматической регулировкой усиления.

Эффект, аналогичный делению мгновенных значений, можно получить, если после усилителей с автоматической регулировкой усиления поставить общий фазовый детектор, используя в качестве опорного напряжение суммар­ного, а в качестве основного — напряжение разностного канала (рис. 2.68). Знак напряжения на выходе фазового детектора учитывает при этом знак раз­ности фаз. В самом деле, наряду с операцией деления может быть использована операции умножения и усреднения полученного напряжения во времени:

Непосредственно основанный на этом фазометр нуждается, однако, в нормировке амплитуд U входных напряжений за счет использования АРУ или ограничения; диапазон однозначного измерения разности фаз составляет при этом π (рис. 2.69). Если же (рис. 2.68) ввести единую автоматическую регули­ровку усиления и суммарного и разностного каналов по выходному напряже­нию суммарного, то выходной эффект умножителя будет поделен на . Диапазон однозначного измерения разности фаз увеличится до 2π.

Потенциальные и реальные точности двухканального моноимпульсного углового измерения

Потенциальная точность двухканального углового измерения, как и одноканального, определяется шумами и особенностями вторичного излучения цели. Наибольший интерес при этом представляет сравнительный анализ двухканальных и одноканальных систем по степени влияния этих факторов на точ­ность измерения.

Оценим ошибку углового измерения двухканальной системы, вызывае­мую шумами. Анализ проведем для антенной системы (рис.2.70) в виде двух сомкнутых излучателей с общей апертурой 2d, полагая, что отклонение на­правления на цель θ от осевого направления антенной системы мало, а величина θ определяется путем измерения разности фаз φ₁-φ₂ принимаемых колеба­ний.

В рассматриваемом случае выражение преобразуется к виду

За счет влияния налагающихся на сигнал шумов фаза результирующего колебания в каждом канале отличается от фазы колебания сигнала. Считая дис­персии отклонения фазы в обоих каналах одинаковыми , диспер­сию разности фаз представим в виде

.

Тогда дисперсия и среднеквадратичная ошибка измерения угловой коор­динаты цели будут

и

Чтобы оценить среднеквадратичное искажение фазы шумовым колебани­ем σ_φ, рассмотрим векторную диаграмму, соответствующую окрестности пика импульса и иллюстрирующую наложение шумового колебания на сигнал одно­го из каналов (рис. 2.71).

Пусть на колебание сигнала, описываемое выражением q cos ωt, наклады­вается колебание помехи ξcos ωt + ηsin ωt, причем . В этом случае величина q имеет смысл отношения сигнал/шум; при измерении фазы после оп­тимальной обработки значение этой величины будет . Из векторной диаграммы следует, что вызванное шумом отклонение фазы δφ при q » 1 опре­деляется величиной , его дисперсия равна , а среднеквадратичное значение .

Таким образом, окончательно имеем

.

Анализируя полученные результаты, убеждаемся, что двухканальные и одноканалъные системы пеленгации с оди­наковыми относительными размерами раскрыва антенн имеют практически одинаковые ошибки, вызываемые дей­ствием шумов.

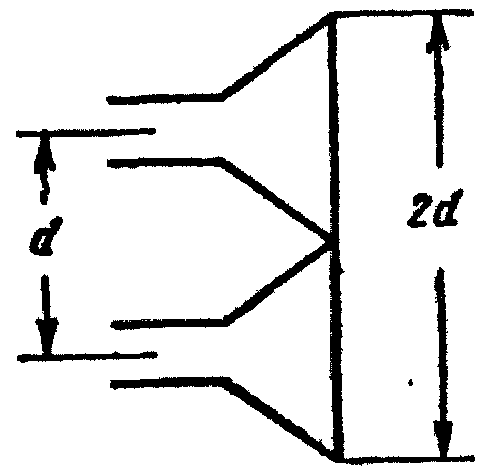
Рис. 2.70. К сравнению одноканальных и двухканальных систем

пеленгации

Рис. 2.71. К расчету шу­мовой ошибки измерения угловой координаты

Наряду с шумами на величину ошибки измерения угловой координаты влияют особенности вторичного излучения цели. Если амплитудные флюктуации сигнала в двухканальных сис­темах не сказываются, то к ошибкам могут вести флюктуации угла прихода («угловой шум») из-за несферичности фазового фронта отраженной волны.

К сказанному следует добавить, что сам по себе полураскрыв антенной системы d еще не является единственной мерой степени сложности ее реализа­ции. В частности, в случае неподвижных антенных систем его можно особенно просто увеличить, переходя к базовой системе с парой сравнительно малых антенн на краях базы.

В случае если b » d, получим

.

При этом разрешающая способность по угловой координате не увеличи­вается, что снижает эффективность использования подобных систем в обычной активной радиолокации с пассивным ответом. Однако в случае радиолокации с активным ответом, когда вместо угловой избирательности может использовать­ся избирательность по форме ответного сигнала, подобные системы могут широко использоваться в целях повышения точности измерения угловой коорди­наты.

Для расширения рабочего сектора наряду с двухантенными измеритель­ными однобазовыми системами могут использоваться четырехантенные систе­мы с двумя взаимно перпендикулярными базами. Подобные системы измерения угловых координат могут использоваться в радиолокационных системах с ак­тивным ответом как при импульсном, так и при непрерывном ответном излуче­нии.