
- •2.1.2. Вывод основных дифференциальных уравнений фильтрации
- •2.1.3. Уравнение баланса энергии в случае многофазной многокомпонентной фильтрации с учетом сил гравитации и капиллярных сил.
- •2.2. Двухмерная двухфазная фильтрация газожидкостной смеси.
- •2.2.1. Основные уравнения и численный метод решения.
- •2.2.2. Решение задачи о разработке газового месторождения с учетом про- движения воды.
- •2.2.3.3. Первоначально рассматривался случай фильтрации газа в однородном по коллекторским свойствам пласте.
- •2.2.3.4. В следующей серии расчетов рассматривалось нестационарная фильтрация газа и воды в неоднородном пласте. Было принято несколько моделей:
- •2.2.4. Об активном воздействии на водонапорный режим
2. ЧИСЛЕННЫЕ МОДЕЛИ ДЛЯ РЕШЕНИЯ ЗАДАЧ РАЗРАБОТКИ ГАЗОВЫХ МЕСТОРОЖДЕНИЙ ПРИ ВОДОНАПОРНОМ РЕЖИМЕ
2.1 МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧ ФИЛЬТРАЦИИ
МНОГОКОМПОНЕНТНОЙ МНОГОФАЗНОЙ СМЕСИ УГЛЕВОДОРОДОВ.
2.1.1. ОБЩИЕ ЗАМЕЧАНИЯ.
Прежде чем сформулировать основные дифференциальные уравнения фильтрации, сделаем ряд общих замечаний, которые будут учитываться в настоящей работе.
При нестационарной фильтрации, как газированной нефти, так и газоконденсатной смеси, как правило, сжимаемость углеводородной жидкости вследствие растворенного в ней газа и сжимаемость чистого газа значительно превосходят сжимаемость породы и жидкости, находящейся в однофазном состоянии. Поэтому сжимаемостью породы обычно пренебрегают. Однако при рассмотрении задач о движении воды с растворенным в ней газом, когда сжимаемости пористой среди и воды вследствие влияния окклюдированного газа становятся соизмеримыми, пренебрегать упругими свойствами породы уже нельзя. В настоящей работе мы будем учитывать как сжимаемость породы, так и сжимаемость жидкой фазы. При этом сжимаемость жидкой фазы происходит как вследствие влияния растворенного в ней газа, так и упругих свойств жидкости, подчиняющихся закону Гука.
Будем также считать, что фильтрация происходит к совершенной скважине и подчиняется закону Дарси. Как правило, нефтяные и газовые скважины являются несовершенными как по степени, так и по характеру вскрытия. При рассмотрении пространственной фильтрации несовершенство по степени вскрытия может быть достаточно полно учтено. Известно, что при нестационарной фильтрации вблизи забоя очень быстро возникает стационарная зона, в которой дебит практически остается постоянным. Поэтому можно рассматривать задачу о нестационарной фильтрации к совершенной скважине с радиусом, на котором несовершенство по характеру вскрытия не сказывается, а в зоне стабилизации - стационарный приток к несовершенной скважине. Следует отметить, что нарушение закона Дарси происходит, в основном, в этой же зоне. Кроме того, нарушение закона Дарси можно учесть введением некоторого нелинейного коэффициента [2].
При использовании обобщенного закона Дарси для описания фильтрации многокомпонентной многофазной смеси вводится понятие фазовой проницаемости. Как показано в ряде исследований [34] , фазовая проницаемость, вообще говоря, оказывается не однозначной функцией насыщенности, а зависит от давления и в случае фазовых переходов от межфазового натяжения при изменении составов фаз. Однако при медленных изменениях давления и состава фаз в процессе нестационарной фильтрации, возможно рассматривать фазовые проницаемости как функции лишь насыщенностей. Вообще говоря, учет влияния межфазного натяжения может быть осуществлен достаточно просто [2, 36, 39]. При использовании однопараметрических зависимостей фазовой проницаемости в случае газированной нефти получаются несколько завышенные значения параметров [34] .
В настоящей работе применяются зависимости фазовых проницаемостей только от насыщенности фаз.
2.1.2. Вывод основных дифференциальных уравнений фильтрации
МНОГОКОМПОНЕНТНОЙ СМЕСИ.
Рассмотрим в начале нестационарное изотермическое многофазное многокомпонентное течение нескольких взаимопроникающих флюидов в системе поровых каналов. Движение такой системы сопровождается непрерывным обменом массами компонентов между фазами.
Уравнения неразрывности (баланса масс) для каждого компонента смеси имеют вид [5, 17]
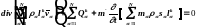 (2.1.1)
(2.1.1)

где
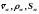 -
скорости фильтрации, плотности,
насыщенности пор фазой
-
скорости фильтрации, плотности,
насыщенности пор фазой  ,
,
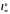 -
массовые концентрации компонента "
-
массовые концентрации компонента "
 "
в фазе
,
"
в фазе
,
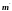 -
пористость пласта в точке,
-
пористость пласта в точке,
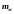 -
пористость, зависящая от фазового
давления,
-
пористость, зависящая от фазового
давления,
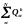 -
плотность источников (стоков) по "
"
компоненту,
-
плотность источников (стоков) по "
"
компоненту,
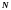 -
число рассматриваемых фаз,
-
число рассматриваемых фаз,
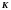 -
число компонентов,
-
число компонентов,
 -
время.
-
время.
Уравнения неразрывности для компонентов дополняются уравнениями движения, связывающими скорости фильтрации фаз с градиентами давления. Согласно обобщенному закону Дарси связь между скоростями фильтрации и градиентами давления имеет вид (с учетом сил гравитации):
 (2.1.2)
(2.1.2)
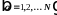
где
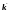 -
коэффициент проницаемости в точке
пласта;
-
коэффициент проницаемости в точке
пласта;
 -
относительная фазовая проницаемость;
-
относительная фазовая проницаемость;
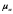 -
коэффициент динамической вязкости
фазы;
-
коэффициент динамической вязкости
фазы;
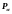 -
давление в фазе;
-
давление в фазе;
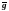 -
вектор силы тяжести (гравитации), который
будем рассматривать как вектор некоторой
массовой силы [32]. Далее предположим,
что поле массовых сил имеет потенциал
-
вектор силы тяжести (гравитации), который
будем рассматривать как вектор некоторой
массовой силы [32]. Далее предположим,
что поле массовых сил имеет потенциал
 .
Тогда
.
Тогда
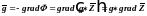 (2.1.2a)
(2.1.2a)
где
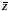 -
глубина залегания точки пласта
-
глубина залегания точки пласта ,
отсчитываемая от некоторой условной
поверхности (ось глубин направлена
вниз).
,
отсчитываемая от некоторой условной
поверхности (ось глубин направлена
вниз).
Обобщенный закон Дарси соответствует предположению, что основное сопротивление течению пропорционально относительным скоростям фильтрации фаз в пористой среде. Условие пропорциональности сил межфазового взаимодействия фазовым скоростям соответствует принципу Онзагера для модели взаимопроникающих континиумов [18].
Комбинируя уравнения неразрывности для каждого компонента смеси с обобщенным законом Дарси для каждой из фаз, получаем систему дифференциальных уравнений, описывающую многофазное изотермическое течение многокомпонентной смеси с учетом фазовых переходов компонентов из одной фазы в другую, сжимаемости породы и флюидов и действия гравитационных и капиллярных сил:
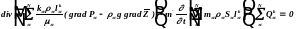 (2.1.3)
(2.1.3)
здесь
-
пористость в точке пласта,
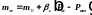 ,
,
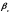 -
коэффициент, учитывающий упругоёмкость
пласта,
-
коэффициент, учитывающий упругоёмкость
пласта,
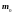 -
коэффициент пористости при атмосферном
давлении
-
коэффициент пористости при атмосферном
давлении
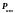 .
.
Система (2.1.3) должна быть дополнена следующими замыкающими соотношениями:
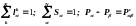 (2.1.4)
(2.1.4)
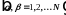
В (2.1.4)
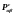 - капиллярное давление между фазами
и
- капиллярное давление между фазами
и 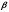 .
При этом
.
При этом
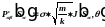 ,
где
,
где
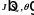 -
безразмерная функция Леверетта,
-
безразмерная функция Леверетта,
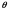 -
контактный угол смачивания [92, 230].
Переменность компонентного состава
фаз при фазовых переходах приводит к
изменению межфазового натяжения
-
контактный угол смачивания [92, 230].
Переменность компонентного состава
фаз при фазовых переходах приводит к
изменению межфазового натяжения
 .
Последнее выражение (2.1.4), вообще говоря,
соответствует условиям статического
равновесия при насыщении порового
пространства. Однако будем считать, что
межфазовый обмен компонентов происходит
при относительном движении фаз так же,
как и в случае их покоя.
.
Последнее выражение (2.1.4), вообще говоря,
соответствует условиям статического
равновесия при насыщении порового
пространства. Однако будем считать, что
межфазовый обмен компонентов происходит
при относительном движении фаз так же,
как и в случае их покоя.
При наличии трех фаз существует по парный контакт трех фаз, а, значит, возникает необходимость в трех зависимостях между капиллярным давлением и насыщенностью. Экспериментально установлено, что капиллярное давление между газовой и водяной фазами можно считать равным сумме капиллярных давлений на границе между нефтяной и газовой фазами и на границе между нефтяной и водяной фазами. Кроме того, капиллярное давление между газовой и нефтяной фазами определяется коэффициентом газонасыщенности, а капиллярное давление между водной и нефтяной фазами - коэффициентом водонасыщенности.
Обычно фазовые проницаемости в случае двухфазной фильтрации получают экспериментально и в дальнейшем аппроксимируют в виде, например, полиномиальных зависимостей от коэффициента насыщенности одной из двух фаз. Совместное движение трех фаз приводит к необходимости использовать фазовые проницаемости для газа, нефти и воды в предположении присутствия всех трех фаз. В этом случае экспериментальное установление таких зависимостей затруднительно. В связи с этим воспользуемся подходом к оценке фазовых проницаемостей трехфазного потока, изложенным в работах Стоуна [43] или Роуза [41]. Этот подход дает, по крайней мере, правильную качественную картину изменения поведения относительных фазовых проницаемостей. При этом считается, что относительная фазовая проницаемость для газа зависит только от коэффициента газонасыщенности, относительная фазовая проницаемость для воды - только от коэффициента водонасышенности, а относительная фазовая проницаемость для нефти, как от коэффициента газонасыщенности, так и от коэффициента водонасыщенности.
При локальном термодинамическом равновесии компонентные составы, а также плотности и вязкости фаз взаимосвязаны условием равенства химических потенциалов отдельных компонентов в сосуществующих фазах. Химический потенциал " "- го компонента в фазе будет зависеть от всего состава фазы и фазового давления. Из-за этого, вообще говоря, потенциалы должны зависеть, помимо состава фаз, также и от насыщенности в терминах капиллярного давления [18]. В пористой среде взаимодействия с твердыми поверхностями также могут влиять на величины химических потенциалов компонентов в фазах. Однако в первом приближении будем пренебрегать влиянием пористой среды на химические потенциалы.
Для закрытой равновесной термодинамической системы, а при локальном термодинамическом равновесии в точке имеет место именно такая система, справедливо правило фаз Гиббса [18, 4]:
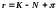 (2.1.5)
(2.1.5)
где
 -
число степеней свободы /независимых
переменных/ системы;
-
число степеней свободы /независимых
переменных/ системы;
-
число компонентов;
-
число фаз;
 -
число внешних параметров /обычно
давление и температура/.
-
число внешних параметров /обычно
давление и температура/.
В случае двух компонентов и двух фаз = 2 и, следовательно, фазовые концентрации, плотности и вязкости фаз зависят только от давления и температуры системы. В случае трех компонентов и двух фаз = 3 и фазовые концентрации, плотности и вязкости уже зависят, помимо давления и температуры, от одной концентрации /или от их комбинации/, например,

Число степеней свободы открытой системы /такая рассматривается в задачах фильтрации/, равняется числу независимых переменных в уравнениях гидродинамики, а поскольку система уравнений должна быть замкнута, то и числу уравнений [4]:
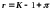 ( 2.1.6)
( 2.1.6)
На практике обычно имеется два случая. Первый - течение нефти, из которой при снижении давления происходит выделение в свободное состояние растворенного в ней газа. Второй - течение углеводородной газовой смеси, для которой характерна ретроградная конденсация, т.е. выпадение жидкой фазы при снижении давления.
Практическое применение математических моделей упирается, с одной стороны, в трудности экспериментальных измерений для фазовых концентраций, плотностей и вязкостей фаз, с другой стороны, в большое число дифференциальных уравнений при использовании расчетных методов определения фазовых концентраций, плотности и вязкости фаз / так называемые "композиционные модели"/. Поэтому приходится применять простые модели, состоящие из двух или трех гипотетических компонентов. При этом возникает проблема сведения сложной многокомпонентной углеводородной смеси к бинарной или тройной гипотетической смеси.
