§ 15. Визначення коефіцієнта теплопровідності ізоляційних матеріалів.

МЕТА: Ознайомити студентів з методами та засобами визначення коефіцієнта теплопровідності і термічного опору сипучих ізоляційних матеріалів та навчитися практично визначати коефіцієнт теплопровідності методом «труби».

1. Прилади та обладнання.

1. Випробувальна труба.

2. Амперметр.

3. Вольтметр.

4. Автотрансформатор.

5. Хромель-алюмелеві термопари (5 штук).

6. Самопишучий 6-точечний потенціометр КСП-4.

7. Мілівольтметр В7-21.

2. Основні теоретичні відомості.

Теплообмін – це процес переносу енергії (в формі теплоти) в просторі з неоднорідними температурним полем. Розрізняють три способи передавання теплоти: теплопровідність, конвекція і випромінювання. При невисоких температурах роль випромінювання невелика і для ізоляційних матеріалів найбільш суттєві втрати енергії (теплоти) будуть ті, які проходять при безпосередньому дотику структурних мікрочастинок.

Теплопередача в широкому розумінні – це перенос теплоти, а більш конкретно – це процес передачі теплоти від одного середовища до іншого через розділяючу стінку.

Теплоносії – це рідкі або газоподібні речовини, які застосовуються для передачі теплоти від тіл з більшою температурою до тіл з меншою температурою. Вони завжди циркулюють у замкнутих системах і використовуються з метою нагрівання і охолодження в теплових і атомних енергетичних установках, системах теплозабезпечення, обладнанні технологічного призначення тощо. Як теплоносії найчастіше використовують гази, водяну пару, воду, а дещо менше – органічні і кремнієвоорганічні сполуки, розплавлені метали, солі, мінеральні масла.

Теплопровідність – це молекулярний перенос теплоти в суцільному середовищі, зумовлений наяністю градієнта температури. При теплопровідності перенос теплоти здійснюється за рахунок співударів та дифузії частинок тіла, а також квантів пружніх коливань їх кристалічної гратки – фононів – при макроскопічній нерухомості всієї маси речовини, тобто вона має атомно-молекулярний характер не пов’язаний з макроскопічним переміщенням в тілі. В чистому вигляді теплопровідність можна спостерігати лише в твердих тілах і в тонких нерухомих шарах рідини та газу. В металах і напівпровідниках теплообмін здійснюється за рахунок співудару і дифузії вільних електронів, а також пружніх коливань кристалічної гратки, тобто в теплопровідність вносять вклад дві складові: електронна і фононова. В металах остання складова низька, в напівпровідниках вона більша, а в діелектриках – є основною. В твердих теплоізоляційних матеріалах, які є діелектриками, механізм теплопровідності зумовлений переносом теплоти фононами - квантами пружніх коливань кристалічної гратки.

Відомо, що при нагріванні тіла кінетична енергія його структурних частинок (вільних електронів, молекул) зростає. Частинки більш нагрітого об’єму тіла співдотикаються при хаотичному русі з сусідніми частинками тіла, віддаючи йому частину своєї кінетичної енергії. Такий процес поширюється по всьому тілу, в результаті чого температура більш нагрітого кінця тіла буде зменшуватися, а в інших ділянках зростатиме до певної величини. При нагріванні тіла температура його в різних точках буде змінюватися з часом і теплота буде поширюватися від зон з вищою температурою до місць з нижчою температурою. У загальному випадку процес передачі теплоти теплопровідністю в твердому тілі супроводжується зміною температури як в просторі, так і в часі:

, (126)

де - координати точки; - час.

Ця функція визначає температурне поле в розглядуваному тілі.

Якщо температура у будь-якій точці тіла змінюється з часом, то температурне поле називається нестаціонарним, а коли температура з часом не змінюється, то поле в даному випадку називають стаціонарним. Поверхня, у всіх точках якої температура однакова, називається ізотермічною. Вектор направлений по нормалі до ізотермічної поверхні в сторону збільшення температури і чисельно дорівнює похідній від температури по цьому напрямку, називають градієнтом температури. За позитивний напрямок градієнта приймається напрямок зростання температури:

. (127)

Частинна похідна використана тут тому, що в загальному випадку температура може змінюватися не лише у просторі, а і у часі (при нестаціонарному режимі).

Тепловий потік – це кількість теплоти, яка передається через довільну поверхню за одиницю часу.

,Вт (128)

де - кількість теплоти в Дж.

Тепловий потік утворюється в результаті різниці температури поверхонь, які співдотикаються.

Питомий тепловий потік або густина теплового потоку – це кількість теплоти, яка передається за одиницю часу через одиницю площадки, яка перпендикулярна напрямку потоку в даній точці або тепловий потік, віднесений до одиниці поверхні тіла:

(129)

Величина є вектором, напрям якого протилежний до напрямку градієнта температури, тому що теплова енергія самостійно поширюється лише в сторону зменшення температури (мал.57).

Мал.57. До пояснення температурного градієнта і теплового потоку.

Стаціонарний режим теплопровідності описується законом Фур’є, який на основі дослідних даних встановлює взаємозв’язок між густиною теплового потоку і градієнтом температури:

, (130)

де - коефіцієнт теплопровідності матеріалу у .

Знак “мінус” свідчить про те, що в напрямку теплового потоку температура зменшується, а величина градієнта температури є від’ємною. Рівняння (130) носить назву основного рівняння теплопровідності.

Коефіцієнт теплопровідності не залежить від градієнта температури, а є фізичним параметром тіла, який характеризує його здатність проводити теплоту. Числове значення визначає кількість теплоти, яка проходить через одиницю ізотермічної поверхні за одиницю часу при умові, що градієнт температури дорівнює одиниці. Коефіцієнт теплопровідності залежить від властивостей матеріалу (густини молекулярної будови, структури, вологості), температури і в незначній мірі від тиску. Але в технічних розрахунках в більшості випадків його визначення для досліджуваного матеріалу приймають сталим, яке дорівнює середньоарифметичному в даних межах зміни температури. Для більшості матеріалів залежність коефіцієнта теплопровідності від температури наближено можна вважати лінійною:

, (131)

де - значення коефіцієнта теплопровідності при температурі = 0°С;

- стала, яка визначається дослідним шляхом;

- температура, при якій визначається .

Найнижчий коефіцієнт теплопровідності мають гази, причому, він збільшується із зростанням температури і становить 0,06…0,6 . Для краплинних неметалевих рідин = 0,07…0,7 і для більшості з них зменшується при зростанні температури. Вода є одним з кращих рідких провідників теплоти. Коефіцієнт теплопровідності води із збільшенням температури зростає до максимального значення 0,7 , а потім зменшується при подальшому збільшенні температури.

Матеріали з < 0,25 називають теплоізоляційними. Коефіцієнт теплопровідності теплоізоляційних і будівельних матеріалів, які мають пористу структуру, при підвищенні температури, зростає за лінійним законом і змінюється в межах від 0,02 до 3,0 . Збільшення пористих матеріалів при зростанні температури пояснюється значним зростанням променевого теплообміну між поверхнями твердого «скелета» пор. Роль конвекції в збільшенні зростає при збільшенні розмірів пор і відповідно повітряних включень. Тому ефективний коефіцієнт теплопровідності пористих тіл має складну природу і є умовною величиною. Крупнопористий матеріал буде менш ефективним теплоізолятором, чим дрібнопористий матеріал з такою ж густиною. Із зростанням вологості матеріалу коефіцієнт теплопровідності значно зростає. Так, для мокрої цегли = 1 , що перевищує значення коефіцієнта теплопровідності як для води, так і для сухої цегли. Підвищення тиску водяної пари при сталій температурі викликає збільшення . Найкращими провідниками теплоти є метали, для яких має значення від 20 до 450 . Коефіцієнт теплопровідності чистих металів, за виключенням алюмінію, з ростом температури зменшується. В металах теплопровідність обумовлено тепловим рухом вільних електронів («електронного газу»), які в три тисячі разів легші за молекули газів. Тому теплопровідність металів набагато більше, ніж газів. Найбільший коефіцієнт теплопровідності мають чисті срібло і мідь.

Для анізотропних матеріалів, які мають не однакову структуру в різних напрямках (деревина, кристали, прокат, пресовані матеріали), теплопровідність залежить від напрямку потоку. Так, в сосні теплопровідність вздовж волокон майже у 2 рази буде більша, чим у поперек.

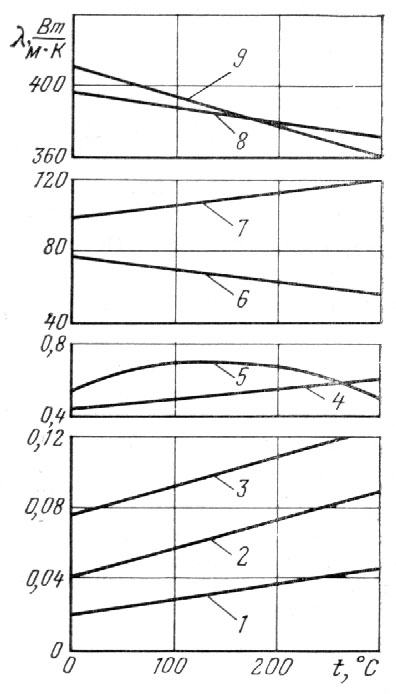
Мал.58. Залежність коефіцієнта теплопровідності від температури: 1-повітря; 2-3-мінеральна вата густиною 150 і 400 ; 4-червона цегла; 5-вода; 6-залізо; 7-латунь (67% Cu, 33% Zn); 8-мідь; 9-срібло.

Значення деяких матеріалів подані в таблиці 38, характер температурної залежності показаний для деяких матеріалів на мал.58.

Величина називається термічним опором стінки. Тоді формула (132) приймає вигляд:

.

Для випадку плоскої стінки (мал.59) формула Фур’є (130) приймає вигляд:

, (132)

де - товщина стінки в м;

, - температури на поверхнях стінок в К.

Мал.59. Розподіл температури в плоскій стінці.

Якщо в чисельнику маємо температурний напір, який в електриці еквівалентний різниці потенціалів, а в знаменнику термічний опір, який еквівалентний опору електричному, то ця формула має аналогію із законом Ома, де замість струму є густина теплового потоку.

Для всіх металів між теплопровідністю і електропровідністю існує кореляція, що зумовлено домінуючим вкладом в передачу як теплоти, так і електроенергії вільних електронів.

Згідно закону Відемана-Франца для всіх металів відношення коефіцієнта теплопровідності до питомої електропровідності прямо пропорційне температурі або:

(133)

де - стала Больцмана;

- заряд електрона;

- питома електропровідність.

Для циліндричної стінки (мал.60) температура змінюється в напрямку потоку за експоненціальним законом:

, (134)

де - довжина циліндра в м;

, - відповідно величина внутрішнього і зовнішнього діаметрів в м.

Термічний опір цієї стінки розраховують за формулою:

(135)

Мал.60. Циліндрична стінка.

Величину експериментально можна визначити методом труби, кулі тощо. В нашому випадку визначається шляхом використання двох телескопічних труб, в просторі між якими засипають випробовуваний матеріал (сипучий) або обгортають ним внутрішню трубу. Всередині труби розміщують електричний нагрівач циліндричної форми, що і породило назву «Метод труби для визначення ».

Таблиця 38

Назва матеріалу	Густина	Температура	Коефіцієнт теплопровідності ,
Азбест листовий	770	30	0,1163
Бетон	2300	20	0,279
Дуб (поперек волокон)	800	20	0,207
Земля волога	1700	17	0,657
Цегла червона	1800	0	0,768
Цегла вогнетривка	1900	0	0,314
Лід	320	0	2,25
Накип котельна	10002500	100	1,3143,14
Пісок сухий	1500	20	0,326
Слюда	290	20	0,582
Сніг	560	-	0,465
Скло	2500	20	0,764
Штукатурка	1600	0	0,698
Алюміній	2670	0	204
Латунь	8600	0	85
Мідь	8800	0	384
Нікель	9000	20	58
Олово	7230	0	64
Ртуть	13600	0	7,9
Свинець	11400	0	35
Срібло	10500	0	458
Сталь вуглецева	1900	20	45
Чавун	7220	20	63
Сажа лампова	165	40	0,166
Вода	999,9	0	0,5513
Повітря	1,293	0	0,0244

При стаціонарному режимі теплового потоку, який проходить через стінки труб за секунду, він чисельно дорівнює теплоті, що виділяється електричним нагрівачем за секунду, тобто дорівнює пружності нагрівача. Розрахункове рівняння теплопровідності при стаціонарному тепловому режимі для циліндричної однорідної одношарової стінки має вигляд:

, (136)

Тоді із рівняння теплового балансу для труби маємо:

.

Звідки знаходимо :

, (137)

де , - відповідно струм в А і напруга електричного кола нагрівача в В;

, - внутрішній і зовнішній діаметр циліндра, утвореного ізоляційним матеріалом, в м;

- довжина циліндра в м;

, - температури внутрішньої і зовнішньої поверхонь ізоляційного циліндра, в К.