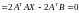- •Электрооборудования и электрического транспорта
- •Оглавление
- •Глава 2 23
- •Глава 3 34
- •Глава 4 43
- •Глава 5 61
- •5.7. Понятие о методах обратного дифференцирования 74
- •Предисловие
- •Глава 1 решение алгебраических уравнений и их систем
- •1.1. Решение систем линейных алгебраических уравнений
- •1.1.1. Итерационные методы решения систем линейных алгебраических уравнений
- •1.1.2. Факторизация и типовые схемы решений
- •1.1.3. Метод Гаусса и lu— разложение
- •1.1.4. Метод Гаусса-Жордана обращения матриц
- •1.1.5. Метод квадратного корня (Холесского)
- •1.1.6. Метод вращений
- •1.1.7. Итерационное уточнение
- •1.1.8. Решение преопределенных систем линейных алгебраических уравнений
- •1.2 Решение систем нелинейных алгебраических уравнений
- •1.2.1. Метод последовательных приближений
- •1.2.2. Метод Ньютона
- •1.2.3. Метод Ньютона по параметру
- •Глава 2 Интерполяция зависимостей
- •2.1. Интерполяция каноническим полиномом
- •2.2. Интерполяция полиномом Лагранжа
- •2.3. Интерполяция полиномом Ньютона
- •2.4. Применение интерполяции для решения уравнений
- •2.5. Интерполяция сплайнами
- •Глава 3 Метод наименьших квадратов
- •3.1. Общие положения
- •3.2. Степенной базис
- •3.3. Базис в виде классических ортогональных полиномов
- •3.4. Базис в виде ортогональных полиномов дискретной переменной
- •3.5. Линейный вариант метода наименьших квадратов
- •3.6. Сглаживание экспериментальных данных с ошибками
- •Глава 4 Определенные интегралы
- •4.1. Классификация методов
- •4.2. Методы прямоугольников
- •4.3. Апостериорные оценки погрешностей по Рунге и Эйткену
- •4.4. Метод трапеций
- •4.5. Метод Симпсона
- •4.6. Методы Ньютона-Котеса
- •4.7. Вычисление интегралов с заданной точностью
- •4.8. Применение сплайнов для численного интегрирования
- •4.9. Методы наивысшей алгебраической точности
- •4.10. Несобственные интегралы
- •4.11. Вычисление кратных интегралов
- •Глава 5 Решение обыкновенных дифференциальных уравнений
- •5.1. Типы задач для обыкновенныхдифференциальных уравнений
- •5.2. Метод Эйлера
- •5.3. Методы Рунге-Кутта
- •5.4. Метод Рунгe-Кутта-Мерсона
- •5.5. Методы Адамса-Башфорта и Адамса-Маултона
- •5.6. Методы Гира
- •5.7. Понятие о методах обратного дифференцирования
- •Библиографический список
- •Методы вычислений в задачах
- •Электроаппаратостроения,
- •Электрооборудования
- •И электрического транспорта
- •346428, Г.Новочеркасск, ул. Просвещения 132
1.1.8. Решение преопределенных систем линейных алгебраических уравнений
Во многих приложениях
возникает необходимость решения
преопределенных систем уравнения, т.е.
таких, в которых число уравнений m
больше числа неизвестных n.
Система уравнений имеет ранг не выше
n,
и точное решение невозможно, поэтому
ищут решение, удовлетворяющее некоторому
критерию качества, причем такое решение,
как правило, не является точным решением
системы. Наиболее широко используется
критерий минимума суммы квадратов
невязок
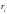 ,
являющихся элементами вектора невязок
R=AX-B
размерности m.
,
являющихся элементами вектора невязок
R=AX-B
размерности m.
Подход к решению переопределенных систем на основе минимизации суммы квадратов невязок получил собирательное название метода наименьших квадратов
Пусть решение
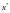 соответствует минимуму суммы квадратов
невязок
соответствует минимуму суммы квадратов
невязок
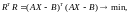
т.е достигает минимума. Такое решение называют нормальным псевдорешением.
Найдем
,
приравнивания нулю производную
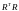 по
x.
При этом необходимо использовать правила
дифференцирования векторов и матриц и
следующие свойства операции
транспонирования:
по
x.
При этом необходимо использовать правила
дифференцирования векторов и матриц и
следующие свойства операции
транспонирования:
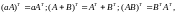
где a – скаляр;A,B, - матрицы или векторы.
В результате преобразований получим:
|
Полученная система уравнений
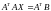
называется нормальной
системой уравнений. Матрица
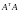 является
нормальной симметричной неотрицательно
неопределенной, причем
является
нормальной симметричной неотрицательно
неопределенной, причем
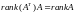 .
.
Нормальная система уравнений может быть решена любым прямым методом. Следует иметь ввиду, что необходимо выполнить большое число операций при перемножении матриц и последующем решении, это может привести к заметному росту ошибок округления.
Для решения предопределенных систем ранга n могут быть использованы численно более устойчивые методы ортогональных вращений и отражений. Алгоритмы решения соответствуют описанным выше алгоритмам для систем полного ранга, однако ортогональные матрицы имеют размерность m x m.
Для использования, например, метода вращения, достаточно в приведенном выше алгоритме перебор по i осуществлять до последний m-й строки матрицы A, а перебор столбцов выполнить для всех столбцов, т.е. для k = 1,2,…,n.
Отметим без доказательства, что в результате решения предопределенных систем методом вращений или отражений получается нормальное произведение.
1.2 Решение систем нелинейных алгебраических уравнений
В подовляющем большинстве случаев математические модели реальных объектов содержат нелинейные функции, их отсутствие в математической модели говорит, как правило, о наличии упрощений.
Решение СНАУ является сложной задачей, необходимо глубокое знание как физических свойств исследуемого объект, так и особенностей СНАУ, используемых для его описания.
Наибольшее распространение получили методы ньютоновского типа, но могут применяется разные варианты последовательных приближений, градиентные методы и.т.п.
СНАУ будем представлять
как приравненную к нулю вектор-функцию
W(x)=0
размерности n,
элементами которого являются функции,
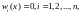 где
x –
вектор искомого решения размерности
n.
где
x –
вектор искомого решения размерности
n.
Например
|
При решении СНАУ,
как правило, возникает проблема
существования и единственности решения,
выбора подходящего решения из множества
решений, удовлетворяющих тождеству
W(X) 0,
если решение существует.
0,
если решение существует.
Для большинства задач точное аналитическое решение не может быть получено, необходимо выполнение последовательности итераций. Важным является способ задания начального приближения, а так же вопрос о том, будет ли сходиться, выбраны метод к одному из решений и насколько быстро.
Говорят, что
последовательность
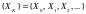 сходится
к
сходится
к
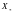 ,
если
,
если
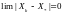 при
при
 .
.
Если существует
константа
![]() и
целое
и
целое
 ,
такие, что для всех
,
такие, что для всех
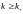
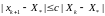 ,
,
то говорят, что
последовательность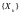 линейно
сходится к
линейно
сходится к
Если данное
неравенство выполняется для некоторых
последовательности
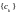 ,
сходящей к нулю, то говорят что
сходитьсясверхлинейнок
,
сходящей к нулю, то говорят что
сходитьсясверхлинейнок
Если
сходится
к
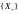 и
существуют постоянные
и
существуют постоянные
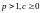
и
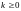 ,
такие , что для всех
,
такие , что для всех
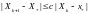
то говорят, что последовательность сходится к с порядком, по меньшей мере равным p. При p=2 говорят о квадратичной скорости сходимости.
Итерационный метод, сходящийся с определенной скоростью к истинному решению при условии, что он стартует в достаточной близости от этого решения, называется локально сходящимися,
Под глобально сходящимися часто понимают методы, в которых обеспечивается сходимость к некоторому решению системы нелинейных уравнений почти из любой начальной точки.