1.1.6. Метод вращений

Матрицы вращений позволяют реализовать упорядоченное исклю­чение переменных.

Построим ортогональную матрицу вращений R₂₁ так, чтобы при левом умножении матрицы, обратной к ней, на матрицуАона обра­щала в ноль элемента₂₁, (исключение переменной x1 из второго урав­нения) затем матрицу R₃₁ для обращения в ноль а и так далее, пока не будут обращены в ноль поддиагональные элементы первого столбца матрицы А:

……………………………………….

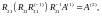
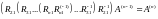
Выполним подобную последовательность операций для всех столбцов матрицы А. Получим факторизацию, на которой основан ме­тод вращений (Гивенса):

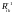Схема выполнения операций выглядит следующим образом

Очевидно, что в результате обратится в ноль элемент .

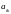Если необходимо решить одну систему уравнений с одной правой частью, то можно использовать следующий алгоритм решения:

1. Для k=1,2,3,…, n -1 выполнить пп. 2,3,4,5.

2. Для i=k+1, k+2,…,n выполнить пп. 3,4,5.

3. Вычислить элементы c и s матрицы вращения

4. Умножить матрицу A слева на , для чего

   1. положить

   2. для j=k+1,k+2,…,n выполнить

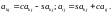
5. Умножить Матрицу на вектор правых частей, для чего выполнить

6. Решить полученную систему уравнений в верхней треугольной форме методом обратной подстановки.

7. Конец алгоритма. Матрица A содержит в верхнем треугольнике матрицу U, вектор B – пересчитан.

Каждый шаг исключений переменной методом вращений из очередного k-го столбца системы уравнений состоит из нескольких малых шагов, на каждом из которых необходимо строит матрицу .

Следует обратить внимание на то, что в отличие от метода Гаусса пересчету на каждом малом шаге подлежат также и элементы ведущей строки 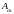c индексами столбцов j, i, k.

В силу ортогональности матриц вращения метод является численно более устойчивым, чем метод Гаусса, однако требует в три раза больше количества операции, причем (n-1)(n-1)/2 операций вызывают функции извлечения квадратного корня. Оценка общего числа необходимых операций приближенно равна .

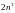Для решения систем с различными правыми частями и одинаковой матрицей A факторизацию выполняют один раз, при этом элементы s матриц вращения запоминают на месте обращаемых в ноль элементов матрицы A. При последующих расчетах элементы c могут быть рассчитаны по формуле , если они не сохранены в специальных массивах данных. При решении нескольких систем с одной матрицей коэффициентов при неизвестных, но различными правыми частями общий объем вычислений сокращается.

1.1.7. Итерационное уточнение

При решении линейных алгебраических систем уравнений большой размерности накапливаются ошибки округления, полученное решение может неприемлемо отличаться от точного решения. В этом случае может быть применено итерационное уточнение, под которым понимают следующий процесс:

1. Решить исходную систему уравнений .

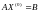2. Вычислить вектор невязок 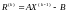. Если все , где - желаемая точность, то расчет закончен и 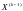есть решение, иначе выполнить пп. 3,4,5.

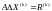3. Решить систему уравнений относительно 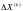- вектора итерационного уточнения.

4. Вычислить уточненное решение .

5. Повотрить пп. 2,3,4,5.

6. Конец алгоритма.

Приведенный алгоритм вытекает из следующих соотношений

.

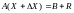Т.к. AX=B, имеем:AX=R.

Следует иметь в виду, что итерационное уточнение сходится, если для матрицы A максимальное собственное число сходимость может быть очень медленной, а при процесс скорее всего расходится.

Недостатком метода итерационного уточнения является необходимость сохранения исходной матрицыА для вычисления вектора невязок, а также увеличение количества операций. Однако в ряде случаев для обеспечения точности расчета итерационное уточнение может быть полезным.