- •Электрооборудования и электрического транспорта
- •Оглавление
- •Глава 2 23
- •Глава 3 34
- •Глава 4 43
- •Глава 5 61
- •5.7. Понятие о методах обратного дифференцирования 74
- •Предисловие
- •Глава 1 решение алгебраических уравнений и их систем
- •1.1. Решение систем линейных алгебраических уравнений
- •1.1.1. Итерационные методы решения систем линейных алгебраических уравнений
- •1.1.2. Факторизация и типовые схемы решений
- •1.1.3. Метод Гаусса и lu— разложение
- •1.1.4. Метод Гаусса-Жордана обращения матриц
- •1.1.5. Метод квадратного корня (Холесского)
- •1.1.6. Метод вращений
- •1.1.7. Итерационное уточнение
- •1.1.8. Решение преопределенных систем линейных алгебраических уравнений
- •1.2 Решение систем нелинейных алгебраических уравнений
- •1.2.1. Метод последовательных приближений
- •1.2.2. Метод Ньютона
- •1.2.3. Метод Ньютона по параметру
- •Глава 2 Интерполяция зависимостей
- •2.1. Интерполяция каноническим полиномом
- •2.2. Интерполяция полиномом Лагранжа
- •2.3. Интерполяция полиномом Ньютона
- •2.4. Применение интерполяции для решения уравнений
- •2.5. Интерполяция сплайнами
- •Глава 3 Метод наименьших квадратов
- •3.1. Общие положения
- •3.2. Степенной базис
- •3.3. Базис в виде классических ортогональных полиномов
- •3.4. Базис в виде ортогональных полиномов дискретной переменной
- •3.5. Линейный вариант метода наименьших квадратов
- •3.6. Сглаживание экспериментальных данных с ошибками
- •Глава 4 Определенные интегралы
- •4.1. Классификация методов
- •4.2. Методы прямоугольников
- •4.3. Апостериорные оценки погрешностей по Рунге и Эйткену
- •4.4. Метод трапеций
- •4.5. Метод Симпсона
- •4.6. Методы Ньютона-Котеса
- •4.7. Вычисление интегралов с заданной точностью
- •4.8. Применение сплайнов для численного интегрирования
- •4.9. Методы наивысшей алгебраической точности
- •4.10. Несобственные интегралы
- •4.11. Вычисление кратных интегралов
- •Глава 5 Решение обыкновенных дифференциальных уравнений
- •5.1. Типы задач для обыкновенныхдифференциальных уравнений
- •5.2. Метод Эйлера
- •5.3. Методы Рунге-Кутта
- •5.4. Метод Рунгe-Кутта-Мерсона
- •5.5. Методы Адамса-Башфорта и Адамса-Маултона
- •5.6. Методы Гира
- •5.7. Понятие о методах обратного дифференцирования
- •Библиографический список
- •Методы вычислений в задачах
- •Электроаппаратостроения,
- •Электрооборудования
- •И электрического транспорта
- •346428, Г.Новочеркасск, ул. Просвещения 132
1.1.2. Факторизация и типовые схемы решений
В ряде случаев решение СЛАУ может быть получено достаточно легко. Рассмотрим шесть важных вариантов вида матрицыА:
А представляет собой матрицу перестановок
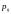 .
Решение
осуществляется путем присваивания
.
Решение
осуществляется путем присваивания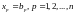 ,
кроме
переменных с индексами iи
,
кроме
переменных с индексами iи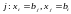 .
.А является ортогональной матрицей, обозначенной через Q. Поскольку Q-1 = =QT, то решение QX = Всводится к формированию QTB; так как Qчасто имеет вид элементарных ортогональных преобразований (вращения, отражения), то алгоритм решения строится простым и достаточно эффективным способом.
А есть невырожденная диагональная матрица D,
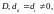 i=
1,2,.. .,0,
i=
1,2,.. .,0,
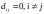 .
Решением DX — В
является
.
Решением DX — В
является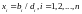 .
Матрицу
Dобычно
хранят в виде вектора, не запоминают
нулевые внедиагональные элементы.
.
Матрицу
Dобычно
хранят в виде вектора, не запоминают
нулевые внедиагональные элементы.
4) А — невырожденная блочно-диагональная матрица DВ, у которой на главной диагонали находятся обратимые блоки размера 2 x 1 или 1 х 1, а вне блоков стоят нули, например:
|

Решение
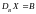 находится
решением соответствующих систем
порядка 2х1 и 1х1.
находится
решением соответствующих систем
порядка 2х1 и 1х1.
5) А есть невырожденная нижняя треугольная матрица. Обозначим ее L, тогда
|
cистема
LX
= В решается
прямой подстановкой: используя первое
уравнение, найти
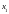 ,
подставив его
во второе уравнение, найти
,
подставив его
во второе уравнение, найти
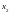 ,
затем подставив
,
х2в
третье уравнение, найти
,
затем подставив
,
х2в
третье уравнение, найти
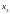 и
т.д.
и
т.д.
6) А есть невырожденная верхняя треугольная матрица, обозначаемая как U. Система UX= Врешается способом обратной подстановки с использованием уравнений от n-го до 1-го для нахождения последовательно неизвестных от хпдо .
В большинстве случаев матрица коэффициентов при неизвестныхАявляется матрицей общего вида, и прямое решение СЛАУ невозможно. Необходимо привести матрицуАк некоторым типовым формам.
Как правило, используется прием факторизации - разложения матриц на множители. Такой прием позволяет не только получить решение СЛАУ, но также дает новые возможности для анализа математических методов, разработки эффективных алгоритмов преобразований и т.п.
Способы представления матриц в виде произведения сомножителей основываются часто на разложении вида
A=A(1)A(2)… A(n), ,
где каждое
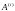 имеет
специальную форму, удобную для решения.
имеет
специальную форму, удобную для решения.
Рассмотрим систему уравнений АХ = В. Пусть матрица А представлена в факторизованной форме, тогда можно выполнить замену переменных
Y1=(A(2)… A(n))x, ,
а затем решить
систему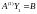 относительно
относительно
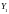 ,
произвести
замену
переменных
,
произвести
замену
переменных
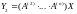 и
решить систему вида
и
решить систему вида
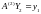 и
т.д., пока не будет получено решение
системы
и
т.д., пока не будет получено решение
системы
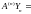 уп-1,
где очевидно
уп-1,
где очевидно
X = Yn.
Методы решения СЛАУ отличаются друг от друга видом множителей А(i) и способом их построения.
Общий подход к решению СЛАУ может быть сформулирован также на основе теории линейных операторов. В этом случае приведение СЛАУ к типовой форме осуществляется путем действия на нее некоторого линейного оператора
О (АХ = В),
в результате получается преобразование СЛАУ
А'Х = В',
гдеА' = ОА, В' = ОВ — преобразованные матрица коэффициентов при неизвестных и вектор правых частей.
Линейный оператор О как правило строится также в виде произведения факторизованных матриц.
Преобразования в прямых методах основаны на исключении неизвестных из некоторых уравнений. Тем или иным способом осуществляется подбор множителей (делителей), на которые умножаются (делятся) строки (столбцы) матрицы А и выполняется операция вычитания, обращающая нужные элементы в ноль.