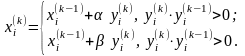Глава 1 решение алгебраических уравнений и их систем

В настоящее время разработано большое количество различных методов решения систем алгебраических уравнений. Для правильно­го выбора метода, наилучшим образом отвечающего сформулирован­ной задаче, необходимо знать особенности его реализации: количество необходимых операций, объем памяти, оценку численной устойчиво­сти, удобство алгоритмизации и т.п.

1.1. Решение систем линейных алгебраических уравнений

Вычислительные методы для решения СЛАУ разделяются на:

• прямые методы, которые позволяют получить точное решение за конечное число операций (при использовании точных вычисле­ний без округлений);

• итерационные методы, которые позволяют после задания неко­торого начального приближения получать в ходе последова­тельности итераций новое приближение к решению до тех пор, пока оно не будет соответствовать заданной точности; общее число операций зависит от исходного приближения вычисли­тельной схемы, особенностей СЛАУ и заранее неизвестно.

Для прямых методов, как правило, стоит проблема численной устойчивости решения, а для итерационных — еще и сходимости по­следовательности итераций к решению.

Далее будем полагать, что СЛАУ представлена в виде

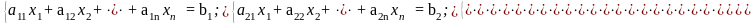
или в матричной форме

АХ = В,

где А — матрица размерности пх п коэффициентов при неизвест­ных; X-— вектор-столбец искомых неизвестных размерности n; В — вектор-столбец свободных коэффициентов (правых частей) размерно­сти п.

1.1.1. Итерационные методы решения систем линейных алгебраических уравнений

Будем полагать, что матрица А невырожденная. В наиболее про­стой форме итерационный метод решения системы АХ = В можно записать в виде вычислительной процедуры:

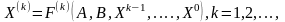
где F^(k)— некоторая последовательность операторов, действующих для заданных A и В.

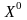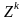Вектор называют начальным вектором (начальным прибли­жением), а векторы = — X, где X— точное решение, на­зывают векторами ошибок. Векторы 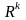= 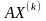- Вназывают векторами невязок.

Широко распространено в литературе по электротехнике описание метода простой итерации, который в развернутой форме имеет следу­ющий вид:

где последовательность k итераций завершается, если все элементы вектора невязок меньше заданной точности расчета 1,2,…,n(получено приемлемое решение), либо превышено зара­нее заданное количество итераций .

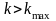В матричной форме

_,

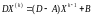где .

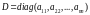Для ускорения сходимости в правой части приведенных выраже­ний возможно использовать не только значения неизвестных х_р, вы­численные на предыдущих итерациях, но также рассчитанные ранее на этой же итерации и имеющие индексы р <i. В этом случае гово­рят о методе ускоренной итерации, часто называемом также мето­дом Гаусса-Зейделя. Схема решения имеет следующий вид:

,

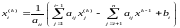_{i=1, 2, …,n; k=1, 2, … .}

В матричной форме

,

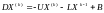где U, L— верхняя и нижняя треугольные матрицы, содержащие нули на главной диагонали, и такие, чтоА — L + D + U.

Метод ускоренной итерации позволяет ограничиться одним масси­вом для хранения искомых переменных.

Существенными вопросом при выборе данных методов для реше­ния конкретных задач является скорость сходимости итерационного процесса к решению, которая зависит от начального приближения и от особенностей матрицы А.

Методы простой и ускоренной итерации сходятся к точному реше­нию, если матрицаАимеет диагональное преобладание. В противном случае решение не гарантировано.

При построении реальных вычислительных схем часто пытаются ускорить процесс решения введением специальных ускоряющих коэф­фициентов.

Тогда полученное значение переменнойx_i^(k) можно скорректировать следующим образом:

где 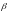_, - коэффициенты ускорения и замедления, часто принимают =1,3, =0,4, - разность решений на двух итерациях.

Таким образом, если направление (знак) приращения переменной не меняется на двух последовательных итерациях, то "движение к ре­шению" пытаются ускорить, в противном случае пытаются подавить колебательный процесс сходимости с помощью уменьшения прираще­ния переменной.

Такой подход требует выполнения дополнительных операций и до­полнительной памяти для хранения вектора приращений переменных Y.