- •Электрооборудования и электрического транспорта
- •Оглавление
- •Глава 2 23
- •Глава 3 34
- •Глава 4 43
- •Глава 5 61
- •5.7. Понятие о методах обратного дифференцирования 74
- •Предисловие
- •Глава 1 решение алгебраических уравнений и их систем
- •1.1. Решение систем линейных алгебраических уравнений
- •1.1.1. Итерационные методы решения систем линейных алгебраических уравнений
- •1.1.2. Факторизация и типовые схемы решений
- •1.1.3. Метод Гаусса и lu— разложение
- •1.1.4. Метод Гаусса-Жордана обращения матриц
- •1.1.5. Метод квадратного корня (Холесского)
- •1.1.6. Метод вращений
- •1.1.7. Итерационное уточнение
- •1.1.8. Решение преопределенных систем линейных алгебраических уравнений
- •1.2 Решение систем нелинейных алгебраических уравнений
- •1.2.1. Метод последовательных приближений
- •1.2.2. Метод Ньютона
- •1.2.3. Метод Ньютона по параметру
- •Глава 2 Интерполяция зависимостей
- •2.1. Интерполяция каноническим полиномом
- •2.2. Интерполяция полиномом Лагранжа
- •2.3. Интерполяция полиномом Ньютона
- •2.4. Применение интерполяции для решения уравнений
- •2.5. Интерполяция сплайнами
- •Глава 3 Метод наименьших квадратов
- •3.1. Общие положения
- •3.2. Степенной базис
- •3.3. Базис в виде классических ортогональных полиномов
- •3.4. Базис в виде ортогональных полиномов дискретной переменной
- •3.5. Линейный вариант метода наименьших квадратов
- •3.6. Сглаживание экспериментальных данных с ошибками
- •Глава 4 Определенные интегралы
- •4.1. Классификация методов
- •4.2. Методы прямоугольников
- •4.3. Апостериорные оценки погрешностей по Рунге и Эйткену
- •4.4. Метод трапеций
- •4.5. Метод Симпсона
- •4.6. Методы Ньютона-Котеса
- •4.7. Вычисление интегралов с заданной точностью
- •4.8. Применение сплайнов для численного интегрирования
- •4.9. Методы наивысшей алгебраической точности
- •4.10. Несобственные интегралы
- •4.11. Вычисление кратных интегралов
- •Глава 5 Решение обыкновенных дифференциальных уравнений
- •5.1. Типы задач для обыкновенныхдифференциальных уравнений
- •5.2. Метод Эйлера
- •5.3. Методы Рунге-Кутта
- •5.4. Метод Рунгe-Кутта-Мерсона
- •5.5. Методы Адамса-Башфорта и Адамса-Маултона
- •5.6. Методы Гира
- •5.7. Понятие о методах обратного дифференцирования
- •Библиографический список
- •Методы вычислений в задачах
- •Электроаппаратостроения,
- •Электрооборудования
- •И электрического транспорта
- •346428, Г.Новочеркасск, ул. Просвещения 132
4.10. Несобственные интегралы
Известно несколько приемов вычисления разных типов несобственных интегралов [1, 2]. Иногда удается заменой переменных перейти от интегралов с бесконечными пределами к интегралам с конечными пределами. Если подынтегральная функция после преобразования останется конечной на новом интервале, то для интегрирования можно использовать методы и программы, рассмотренные в предыдущих разделах. Довольно распространенным является способ образования верхнего предела интегрирования, при котором исходный несобственный интеграл разбивается на сумму двух интегралов:
. |
Затем оценивается аналитически, а иногда и численными методами модуль вторго интеграла, и при выполнении условия
|
в качестве приближенного значения несобственного интеграла выбирается величина интеграла в пределах [0,b].
Для вычисления
несобственных интегралов с бесконечными
пределами применимы и квадратурные
формулы Гаусса- Кристоффеля (4.46), узлы
и веса которых определяются в зависимости
от вида весовой функции
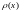 ,
входящей под интеграл в форме произведения
,
входящей под интеграл в форме произведения
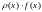 .
.
Так, для интегралов
в пределах [ ]
при
]
при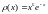 узлами
квадратурной формулы (4.46) являются корни
многочленов Лаггера
узлами
квадратурной формулы (4.46) являются корни
многочленов Лаггера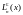 ,
а весовые коэффициенты
,
а весовые коэффициенты
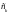 определяются
через интеграл [2]:
определяются
через интеграл [2]:
|
где n – выбранное число узлов.
Как правило, в программах используют заранее вычисленные узлы и веса квадратурных формул, задаваемых в виде констант. В справочниках [10,18] имеются достаточно подробные таблицы узлов и весов квадратурных формул Гаусса-Кристоффеля для различных видов функции p(x) и различных чисел n.
Для интегралов в
пределах
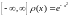 узлами
квадратурной формулы (4.46) будут корни
многочленов Эрмита
узлами
квадратурной формулы (4.46) будут корни
многочленов Эрмита
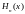 ,
а весовые коэффициенты определяются
по формуле, аналогичной (4.54), где интеграл
необходимо взять в бесконечных пределах.
,
а весовые коэффициенты определяются
по формуле, аналогичной (4.54), где интеграл
необходимо взять в бесконечных пределах.
Несобственные
интегралы с конечными пределами
интегрирования, но с подынтегральной
функцией, обращающиеся в бесконечность
в отдельных точках интервала [a,b],
вычисляют методами аддитивного или
мультипликативного выделения особенностей,
а также построения нестандартных
квадратурных формул [2]. При аддитивном
способе выделения особенности
подынтегральную функцию представляют
в виде суммы двух функций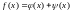 ,
где
-
ограниченная функция;
,
где
-
ограниченная функция;
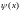 -
интегрируется аналитическими методами.
Для мультипликативного способа функция
f(x)
представляется в виде произведения
-
интегрируется аналитическими методами.
Для мультипликативного способа функция
f(x)
представляется в виде произведения
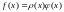 ,
где
-
ограничена;
- положительная и интегрируемая на
отрезке [a,b]. Тогда можно применить
квадратурные формулы Гаусса-Кристоффеля,
которые требуют вычисления в узлах
функции
,
при этом
рассматривается
как весовая функция.
,
где
-
ограничена;
- положительная и интегрируемая на
отрезке [a,b]. Тогда можно применить
квадратурные формулы Гаусса-Кристоффеля,
которые требуют вычисления в узлах
функции
,
при этом
рассматривается
как весовая функция.
4.11. Вычисление кратных интегралов
В общем виде задача приближенного вычисления кратного интеграла формулируется так же, как и задача приближенного вычисления однократного интеграла, только полные производные заменяются частными производными, а узловые точки промежутка [a,b] - узловыми точками в области , по которой ведется интегрирование. Как и в случае однократного интеграла, величина интеграла заменяется линейной комбинацией значений интегрируемой функции в конечном числе точек области интегрирования , а именно:
|
где
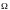 -
область интегрирования;
-
область интегрирования;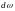 -
элемент объема области;
-
элемент объема области;
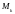 -
узловые точки, причем
-
узловые точки, причем
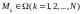 .
.
На случай вычисления кратного интеграла полностью переносятся приведенные выше методы вычисления однократного интеграла, с той разницей, что для кратных интегралов квадратурные формулы будут несколько сложнее и число их будет больше , так как из различных соображений интегрирование по разным переменным можно вести по разным квадратурным формулам.
Для вычисления двойного интеграла в случае квадрата может быть использована формула
, |
а при вычислении тройного интеграла в случае куба
, |
для схемы суммирования подобной (4.46).

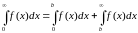
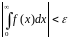
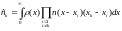 ,
(4.54)
,
(4.54)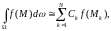 (4.55)
(4.55)