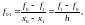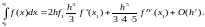4.4. Метод трапеций

Подинтегральную функцию заменим на участке полино­мом первой степени . Как и в методах прямоугольников, такая аппроксимация неоднозначна. Одним из возможных способов являет­ся проведение прямой через значения функции на границах интервала интегрирования (рис. 4.4). В этом случае приближенное значение интеграла определяется как площадь трапеции:

(4.19)

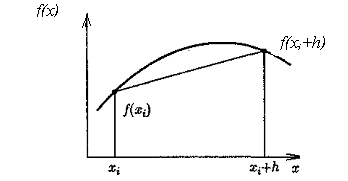
Рис. 4.4. Метод трапеций

Априорную погрешность Rметода трапеций получим путем инте­грирования тейлоровского разложения подынтегральной функции око­ло точки x_i.

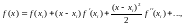(4.20)

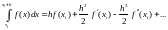. (4.21)

С помощью разложения (4.20) вычислим подынтегральную функ­цию в точке :

,

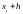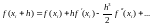откуда

. (4.22)

Подставляя произведение (4.22) в выражение (4.21), получим

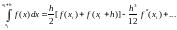(4.23)

Следовательно, главный член погрешности метода трапеций на одном интервале будет

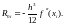(4.24)

Если интегрирование проводится путем разбиения отрезка [x₀;x_п] на несколько интервалов, то общую погрешность получим суммирова­нием частичных погрешностей (4.24):

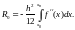(4.25)

Получили, на первый взгляд, несколько неожиданный результат. Оказалось, что метод трапеций имеет погрешность в два раза боль­ше по абсолютной величине, чем метод средних прямоугольников, хо­тя аппроксимация подынтегральной функции проводилась полиномомпервой, а не нулевой степени. По-видимому, выбранный вариант ап­проксимации подынтегральной функции прямой, проходящей через ее значения на границах, не является оптимальным. Задача выбора спо­соба аппроксимации полиномом заданной степени с наименьшей воз­можной погрешностью была решена Гауссом, что привело к развитию целого класса методов.

Как видно из выражения (4.25), метод трапеций, как и метод сред­них прямоугольников, имеет второй порядок. Если подынтегральная функция задана аналитически, то предпочтительнее из методов второ­го порядка применять метод средних прямоугольников вследствие его меньшей погрешности.

4.5. Метод Симпсона

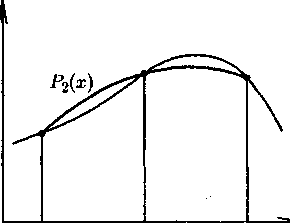
Подынтегральную функцию f(x) заменим интерполяционным по­линомом второй степени Р₂(х) — параболой, проходящей через узлы (рис. 4.5), тогда

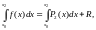
где R— погрешность вычисления интеграла.

P

x₀ x_i x₂ X

Рис. 4.5. Метод Симпсона

Для записи полинома Р₂(х) воспользуемся интерполяционной фор­мулой Ньютона (2.6) для трех узлов:

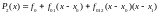, (4.26)

где и — разделенные разности, определяемые по формулам

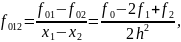
h- расстояние между узлами.

Введем новую переменную , тогда и полином(4.26) принимает вид

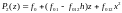. (4.27)

Теперь вычислим интеграл от полинома (4.27):

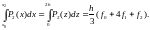(4.28)

Последнее соотношение называют квадратурной формулой Симпсона или формулой парабол.

Формулу Симпсона можно получить и с помощью первой и второй формул Рунге, примененных к вычислению интеграла методом трапе­ций. Запишем два приближенных значения интеграла от функции f(x) на интервале [ , ] с шагами hи 2hпо формуле трапеций (4.19):

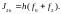(4.29)

Интегралы (4.29) подставим в формулы (4.14) и (4.15) и получим уточненное значение интеграла

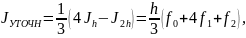
которое совпадает с формулой Симпсона (4.28).

Для оценки погрешности формулы Симпсона разложим подынте­гральную функцию f(x) в ряд Тейлора около точки х₁и проинтегриру­ем разложение почленно на интервале [ , ]:

(4.30)

Суммируя разложения около точки х₁для функции f(x) в узлах x₀ иx₂, получим, что

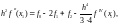
тогда интеграл (4.30) принимает вид

. (4.31)

Первое слагаемое в правой части формулы (4.31) совпадает с форму­лой Симпсона значит, второе слагаемое является главным членом по­грешности для интеграла на интервале [ , х₂]

(4.32)

Если интеграл вычисляется на интервале [ , ] путем разбиения его на четное число подинтегралов [ ], на каждой паре которых применяется формула Симпсона для узлов , то полная по­грешность будет суммой правых частей соотношения (4.32). При ма­лой величине шага hна основании метода средних прямоугольников получим

тогда полная погрешность запишется в виде

(4.33)

следовательно, формула Симпсона имеет четвертый порядок точности с очень малым численным коэффициентом в остаточном члене. Фор­мула Симпсона позволяет получить высокую точность, если четвертая производная подынтегральной функции не слишком велика. В против­ном случае методы второго порядка могут дать большую точность, чем методСимпсона. Например,[17]дляфункции 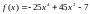формула трапеций при n = 2 для интеграла в пределах [-1,1] дает точный результат, равный 4, тогда как по формуле Симпсона получим результат, не совпадающий даже по знаку (-8/3).