3.6. Сглаживание экспериментальных данных с ошибками

Если некоторый набор экспериментальных данных содержит слу­чайные отклонения, а зависимость ( ) задана значениями f_tдля рав­ноотстоящих абсцисс , то по ряду можно уточнить значения орди­нат, т.е. провести сглаживание зависимости ( ).Сглаженные орди­наты записываются в виде φ_i.

Л инейное сглаживание для пточек по трем ординатам проводится с помощью формул:

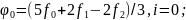
(3.26)

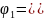
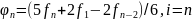
Линейное сглаживание по пяти ординатам проводится по форму­лам:

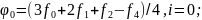
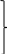
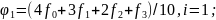
(3.27)

.

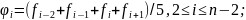
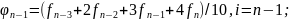
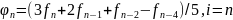Для функций ƒ_i (x_i), сильно отличающихся от линейных, использу­ется нелинейное сглаживание с помощью полиномов высоких степеней m. При m= 3 необходимое число координат составляет семь. Сгла­живание при семи ординатах производится по формуле:

φ_i = (a₁ƒ_i-3 + a₂ ƒ_i-2+ a₃ ƒ_i-1 + a₄ ƒ_i + a₅ ƒ_i+1 +a₆ ƒ_i+1 +a₇ ƒ_i+3)/42, (3.28)

где коэффициенты a₁ - a₇берутся из табл. 3.2 в зависимости от но­мера ординаты.

Таблица 3.2. Коэффициенты формулы (3.28)

i	a1	a2	a3	a4	a5	a6	a7
0	39	8	-4	-4	2	4	-2
1	8	19	16	6	-4	-7	4
2	-4	16	19	12	2	-4	1
3	-4	6	12	14	12	6	-4
4	-4	6	12	14	12	6	-4
n-2	1	-4	2	12	19	16	-4
n-1	4	-7	-4	6	16	19	8
n	-2	4	1	-4	-4	8	3

Глава 4 Определенные интегралы

4.1. Классификация методов

Ставится задача вычислить интеграл вида

b

J = ∫ƒ(x)dx, (4.1)

a

где aи b— нижний и верхний пределы интегрирования; ƒ(x) — непре­рывная функция на отрезке [а, b].

К численному интегрированию обращаются, когда нельзя через эле­ментарные функции аналитически записать первообразную интеграла (4.1) или когда подобная запись имеет сложный вид.

Сущность большинства методов вычисления определенных инте­гралов состоит в замене подынтегральной функции ƒ(x)аппроксими­рующей функцией φ(x), для которой можно легко записать первооб­разную в элементарных функциях, т.е.

b b

∫ƒ(x)dx = ∫φ(x)dx + R = S + R, (4.2)

а а

где S— приближенное значение интеграла; R— погрешность вычис­ления интеграла.

Используемые на практике методы численного интегрирования мож­но сгруппировать в зависимости от способа аппроксимации подын­тегральной функции. Дадим краткую характеристику групп наиболее распространенных методов.

Методы Ньютона-Котеса основаны на полиномиальной аппрокси­мации подынтегральной функции. Методы этого класса отличаются друг от друга степенью используемого полинома, от которой зависит коли­чество узлов, где необходимо вычислить функцию ƒ(x). Алгоритмы ме­тодов просты и легко поддаются программной реализации.

Сплайновые методы базируются на аппроксимации подынтеграль­ной функции сплайнами, представляющими собой кусочный полином.

Методы различаются по типу выбранных сплайнов. Такие методы име­ет смысл использовать в задачах, где алгоритмы сплайновой аппрок­симации применяются для обработки данных.

В методах наивысшей алгебраической точности (методы Гаусса-Кристоффеля и др.) используют неравноотстоящие узлы, расположен­ные по алгоритму, обеспечивающему минимальную погрешность ин­тегрирования для наиболее сложных функций при заданном количе­стве узлов. Методы различаются способами выбора узлов и широко используются для интегрирования, в том числе они применимы и для несобственных интегралов. Хотя из-за необходимости хранения чи­словых констант и стандартизации пределов интегрирования програм­мы указанных методов требуют несколько большего объема памяти по сравнению с методами Ньютона-Котеса.

В методах Монте-Карло узлы выбираются с помощью датчика слу­чайных чисел, ответ носит вероятностный характер. Методы оказыва­ются эффективными при вычислении интегралов большой кратности.

В класс специальных группируются методы, алгоритмы которых разрабатываются на основе учета особенностей конкретных подын­тегральных функций, что позволяет существенно сократить время и уменьшить погрешность вычисления интегралов.

Независимо от выбранного метода в процессе численного интегри­рования необходимо вычислить приближенное значение Sинтеграла и оценить погрешность R (4.2). Погрешность будет уменьшать­ся при увеличении количества разбиений N интервала интегрирования [а, b]за счет более точной аппроксимации подынтегральной функции, однако при этом будет возрастать погрешность за счет суммирования частичных интегралов, и последняя погрешность с некоторого значе­ния No становится преобладающей (рис. 4.1) [1,16].

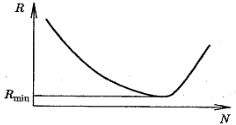
Рис. 4.1. Зависимость полной погрешности Rот количества разбиений N интервала интегрирования

Это обстоятельство должно предостеречь от выбора чрезмерно большого числа N и привести к необходимости разработки способа оценки погрешности Rвыбранного метода интегрирования.