I,j,k : IntType;

Begin

{Обратный ход}

k:= 0;

For i:=1 to N do

begin

X[i]:= B[i]/A[i,i];

k:= k+1;

{Заполнение Form1.ProgressBar2}

Form1.ProgressBar2.Position:=Round(100*k/N);

end;

End; {Solution}

procedure Jordan(N:IntType;Var A:TMatrix; Var B:TVector; Var X:TVector);

{Реализация метода Жордана}

Var

I, j, k : IntType;

S : String;

Flag : Boolean;

begin

Form1.Memo1.Visible:= True;

Form1.Memo1.Clear;

FactorizJordan(N,A,B); {Факторизация}

SolutionJordan(N,A,B,X); {Решение}

Form1.Memo1.Lines.Add('Решение СЛАУ методом Жордана');

For i := 1 to N do

Form1.Memo1.Lines.Add(Format('X[%d] = %f', [i, X[i]]));

For i:= 1 to N do

Form1.StringGrid1.Cells[N+3, i]:= FloatToStrF(1.0*X[i],ffGeneral,3,3);

end;

1.1.6.8. Факторизация

Матица коэффициентов может быть разложена в произведение нижней треугольной и верхней треугольной матриц, т. е.

,

при условии, что и её верхние левые главные подматрицы не вырождены. Кроме того, если симметрична, то верхняя треугольная матрица является транспонированной по отношению к нижней треугольной матрице, и у обеих этих матриц на главной диагонали находятся единицы. Таким образом,

.

По очевидным причинам, это разложение часто называют тройной факторизацией. Используя данное представление, можно решить матричное уравнение системы за два шага

,

где

.

Сначала решается первое уравнение относительно , а затем второе уравнение относительно . Элементы матриц и могут быть вычислены по формулам

,

,

где сумма полагается равной нулю, если верхний предел суммирования меньше нижнего. Векторы и определяются по формулам

,

,

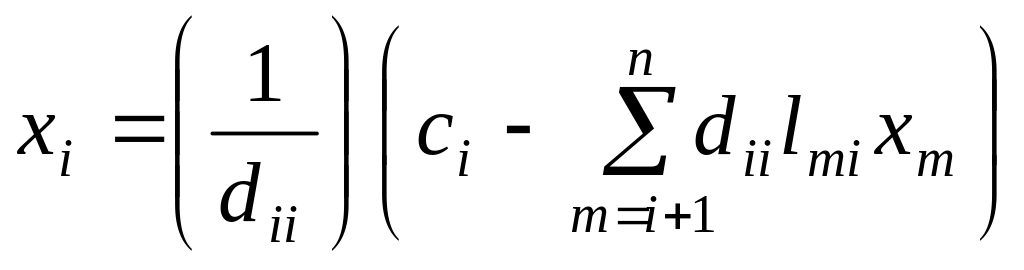где – размерность квадратной матрицы коэффициентов .

Разложение может быть выполнено весьма эффективно посредством вычисления элементов и по столбцам. Эта процедура предпочтительнее простого метода исключения Гаусса, так как она значительно более быстрая.

1.1.6.9. Преобразование Хаусхолдера.

Пусть w – некоторый фиксированный вектор (столбец) евклидова пространства со скалярным произведением , такой, что

Образованная с его помощью – матрица

называется матрицей Хаусхолдера.

Чтобы выявить простейшие геометрические свойства преобразования Хаусхолдера, осуществляемого посредством матрицы , посмотрим, что представляет собой вектор , служащий при этом преобразовании образом произвольного вектора :

Если взять коллинеарным , т.е. , где , то имеем . В таком случае, получаем

Если же перпендикулярно , то и, значит, что .

Итак, преобразование Хаусхолдера действует на векторы -мерного евклидова пространства следующим образом: векторы, ортогональные определяющему матрицу Хаусхолдера вектору w, оно оставляет неизменными, а векторы, коллинеарные w, переводит в противоположные – отражает. Отсюда проистекают другие названия матрицы и соответствующего ей преобразования – матрица и преобразование отражения.

Непосредственным перемножением вектора на вектор находим:

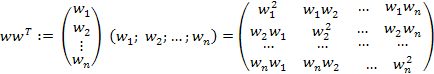
Очевидная симметричность матрицы влечет симметричность матрицы . Пользуясь этим, имеем

(поскольку , в силу (1.1.1)). Полученное в итоге равенство означает, что матрица Хаусхолдера – ортогональная.

Одним из важнейших свойство ортогональных преобразований является сохранение длин преобразуемых векторов. Благодаря этому свойству, согласно вышепоказанному, можно утверждать, что

,

Равенство играет существенную роль для конкретизации векторов при построении матриц Хаусхолдера, таких, чтобы преобразованиями с их помощью достичь определенных целей.