Комбинаторика Несколько слов о рекуррентных соотношениях для перестановок.
I-ое рекуррентное соотношение:
……………………….…………………….
II-ое рекуррентное соотношение:
……………………………………..……….
Перестановки с повторениями.
В
B
=
элементов
если
.
Т.е.
множество выбираемых элементов
(
элементов), которое разбито на
классов
,
причем i-ый
класс содержит ni
элементов.
Перестановки из элементов данной спецификации называют перестановками с повторениями.
Оценим число перестановок с повторениями
Если переставлять буквы слова «мама», то поменяв местами буквы «м» и «а» мы ничего не изменим.
м
ама
Для
вычисления
заменим в множестве B
элементы класса
на
элементы, которые различны
между собой
между всеми элементами множества B. Тогда число возрастает в
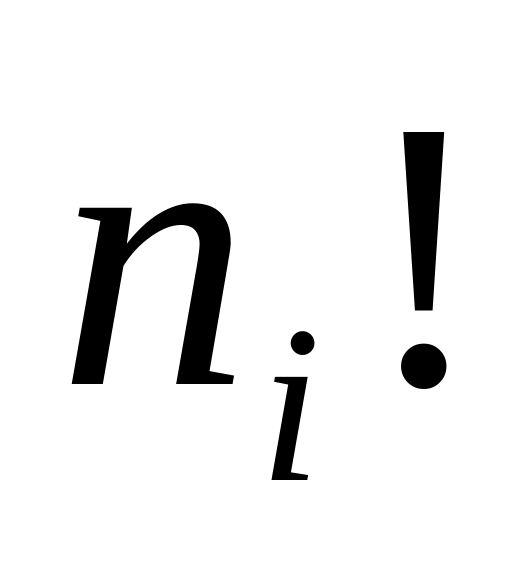раз (по правилу умножения)
Проделаем
эту процедуру для
,
т.
к. после замены все элементы в B
стали различные и их можно переставить
способами.
Перестановки с неограниченными повторениями.
Имеем n различных элементов. После выбора элемента на его место становится точно такой же элемент из запаса, т.е. после выбора каждого элемента ситуация полностью восстанавливается.
Перестановки при спецификации элементов называются перестановки с неограниченными повторениями.
r раз
Пусть имеем n различных элементов.
Чем сочетания отличаются от перестановок?
Перестановки – упорядоченная выборка.
Сочетания – неупорядоченная выборка.
любая
неупорядоченная выборка из Г
элементов
та же самая, но уже упорядоченная выборка
r!=
количество способов упорядочивания
! Неупорядоченную г-выборку можно упорядочить r! способами.
! Договариваемся
Комбинаторного смысла это не несет.
Рассмотрим
Рекуррентные соотношения для сочетаний.
(o
o
…
o
) B
Сочетания разбиваем на два типа: сочетания, содержащие элемент
элемент в выборку входит,
и сочетания, не содержащие элемент
из
B
надо взять r
элементов
элемент взяли из B
Т.к. мы разбили число сочетаний на два класса (т.е. на два непересекающихся множества), то
при
n>r
Рекуррентное соотношение для числа сочетаний.
Вспомним
формулу
Свойства
числа
Таблица
n\r |
0 |
1 |
2 |
3 |
4 |
0 |
1 |
|
|
|
|
1 |
1 |
1 |
|
|
|
2 |
1 |
2 |
1 |
|
|
3 |
1 |
3 |
3 |
1 |
|
4 |
1 |
4 |
6 |
4 |
1 |
Из таблицы следует, что:
- Число сочетаний в каждой строке таблицы совпадают с коэффициентами разложения выражения (1+t)n по биному Ньютона
- Число сочетаний имеют свойство симметрии
