3.2 Исследование напряжений при давления на одном из контуров

1. Сжимающее радиальное давление на наружном контуре. По формулам (3.7), положив в них р_В = 0, найдем

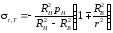. (3.9)

Второй член в скобке формулы (3.9) равен единице или меньше ее, поэтому напряжения 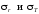во всех точках отрицательные, сжимающие. Окружное напряжение по абсолютной величине всегда больше радиального. Наибольшее нормальное радиальное напряжение _r возникает на наружной поверхности трубы (r = R_н) и равно р_н, а наибольшее окружное напряжение 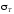на внутренней поверхности (r = R_B) и равно 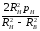. Как видно из формулы (3.9), напряжения меняются вдоль радиуса по кри­волинейному закону. 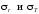Эпюры напряжений показаны на рис. 31,а. Уменьшение наружного радиуса может быть опреде­лено по формуле (3.8) для перемещения v, если положить в ней р_В = 0, а r = R_B. Тогда

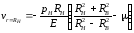. (3.10)

2. Сжимающее радиальное давление на внутреннем контуре. По формуле (3.7), положив в р_н = 0, найдем

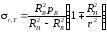. (3.11)

а б

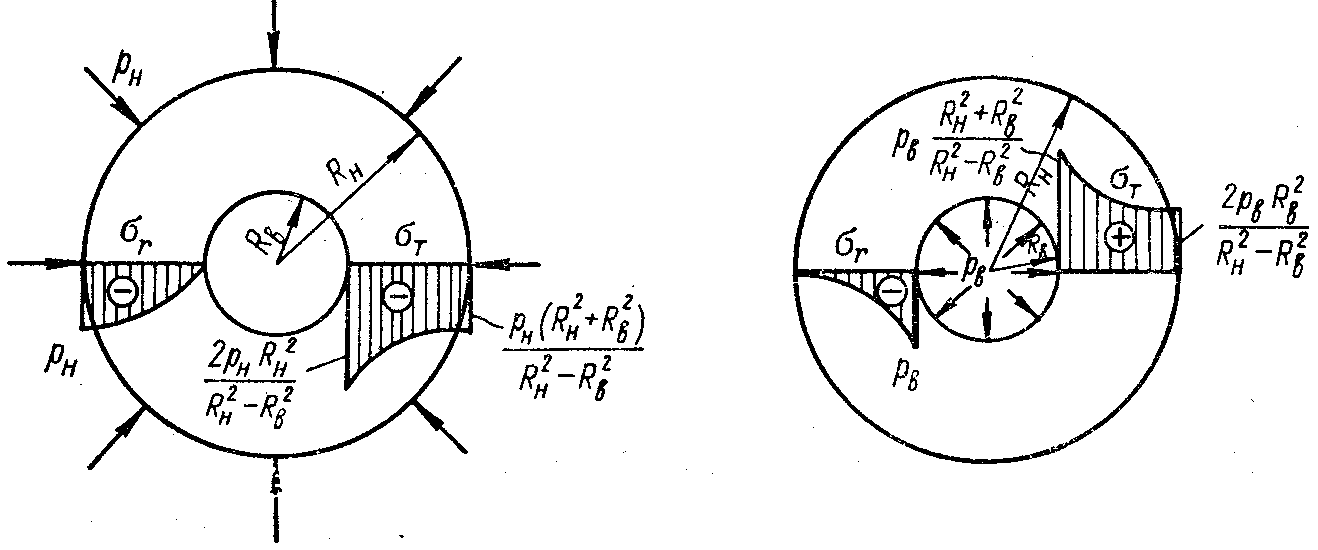
Рис. 31

Второй член в скобке формулы (3.11) равен единице или больше ее, поэтому напряжения _r во всех точках трубы отри­цательны, а 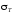положительны. Наибольшее нормальное ради­альное напряжение _r возникает на внутренней поверхности (r = R_B) и равно р_B, наибольшее окружное 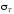также на вну­тренней (r = R_B), оно растягивающее и равно .

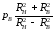Закон изменения напряжений вдоль радиуса тоже криволи­нейный [см. формулу (3.11)]. Эпюры напряжений 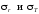показаны на рис. 31,б. Увеличение внутреннего радиуса может быть по­лучено по формуле (3.8) для перемещений v, если положить в ней р_н = 0, a r = R_B:

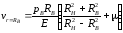. (3.12)

Соотношение окружных напряжений, вычисленных по фор­муле (3.11) при r = R_B и r == R_H ,

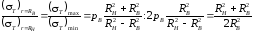. (3.13)

Из формулы (3.13) видно, что чем меньше толщина кольца, т. е. чем ближе друг к другу значения R_B и R_H , тем ближе отно­шение (3.13) к единице, т. е. тем равномернее распределяются напряжения _T по толщине трубы. Например, при R_B = 0,95, отношение

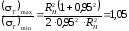
и окружные напряжения можно считать равномерно распределен­ными по толщине кольца. При большой толщине трубы напря­жения _r и _T в точках, удаленных от внутренней поверхности, сближаются по величине и в пределе, при R_H , становятся одинаковыми и противоположными по знаку.

Представим формулу (3.11) в виде

.

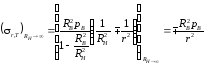Следовательно, если r > 4R_B, напряжения _r и _T будут равны и будут составлять меньше 6% от внутреннего давления. На этом основании по формуле (3.11) можно определять радиальные и окружные напряжения в случае плоской деформации тела, имею­щего отверстия, нагруженные радиальным давлением, располо­женные друг от друга на расстоянии больше 8R_B (рис. 32). Внеш­ний контур тела не имеет значения и может быть произвольного очертания.

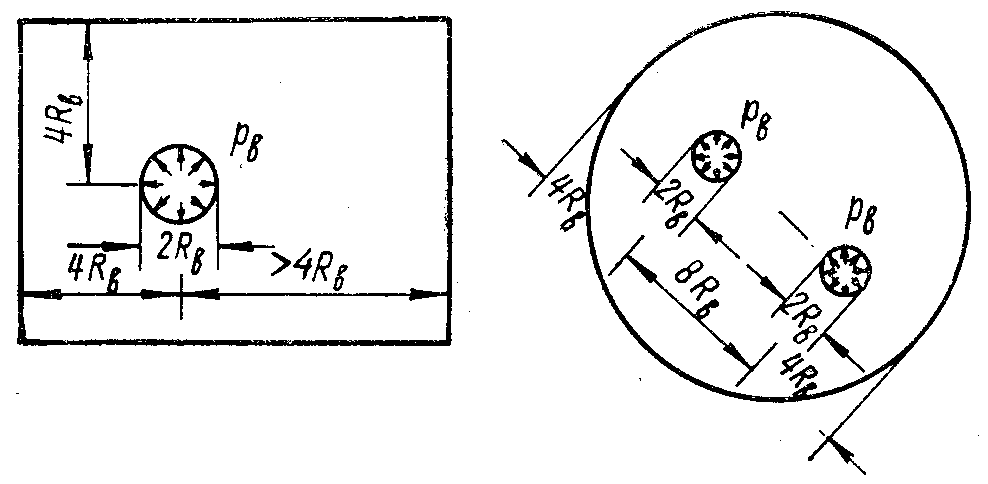
Рис. 32

3.3 Условия прочности при упругой деформации

Составим условия прочности для толстостенной трубы, испы­тывающей внутреннее давление р_В. В зависимости от принятого предельного состояния для наиболее напряженной точки на вну­тренней поверхности трубы получим следующие выражения:

1. Для хрупких материалов (чугун, бетон) по первой теории прочности

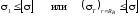. (3.14)

По формуле (3.11) при r = R_B расчетное напряжение

.

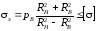или

,

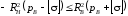откуда

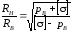. (3.15)

Выражение (3.15) показывает, что при внутреннем давлении, при­ближающемся по величине к допускаемому напряжению [], от­ношение 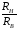стремится к бесконечности, т. е. никаким увели­чением наружного радиуса R_H нельзя удовлетворить условию прочности (3.14).

2. Для пластичных материалов (сталь, медь) по третьей теории прочности

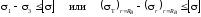. (3.16)

По формуле (3.11) при r == R_B расчетное напряжение

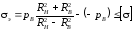. (3.16)

или

,

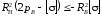откуда

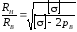. (3.17)

Выражение (3.17) показывает, что при внутреннем давлении р_В, приближающемся по величине к половине допускаемого напря­жения [], отношение 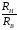стремится к бесконечности и увели­чением наружного радиуса Р_H удовлетворить условию проч­ности (3.16) нельзя.