1.7 Относительная линейная деформация в произвольном направлении

Наметим внутри упругого тела две точки А (х, у, z) и В (х + dx, у + dy, z + dz), находящиеся на расстоянии dr друг от друга (рис. 13). Направляющие косинусы отрезка dr обозначим l, т и п.

Рис. 13

При деформации тела под влиянием внешней нагрузки, точка А перейдет в положение А₁, точка В в положение В₁, а отрезок dr получит приращение . Новая длина отрезка АВ

,

где _r – искомая относительная линейная деформация.

Проекции перемещения АА₁ точки А на оси координат обоз­начаем и, v и w. Тогда проекции перемещения ВВ₁ точки В на оси координат и + du, v + dv, w + dw.

С одной стороны

(A₁B₁)² = dr²(1+_r)² dr²(1+2_r).

С другой стороны, квадрат отрезка А₁В₁ равен сумме квадратов трех его проекций на оси координат:

(А₁В₁)² = dx² + dy² + dz² + 2dxdu + 2dydv + 2dzdw.

Тогда получим

.

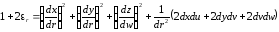Подставив выражения для полных дифференциалов переме­щений и, v и w, и заметив, что

учитывая, что l² + m² + п² = 1, сокращая на 2, и используя зависимости (1.15), получаем

. (1.16)

Сравнение выражений (1.16) для линейной деформаций _r, и (1.6) для нормального напряжения _N в том же направлении, показы­вает, что они по структуре одинаковы и выражение (1.16) может быть получено из формулы (1.6) путем замены с сохранением знач­ков на и на . Пользуясь такой заменой, можно получить все формулы теории деформации из аналогичных формул теории напряжений. В ча­стности, деформированное состояние в точке упругого тела опре­деляется матрицей компонентов тензора деформаций:

.

1.8. Уравнения совместности деформаций

Из уравнений (1.15) видно, что если заданы три функции и, v и w, то все шесть составляющих деформаций будут определены однозначно. Но задать эти шесть составляющих произвольно нельзя. Они должны быть связаны дополнительными зависимостями — уравнениями совместности.

Из допущения о сплошности тела следует, что перемещения в его точках должны представлять собой непрерывные и одно­значные функции от координат. Для таких функций величина их производных не зависит от порядка дифференцирования. Поэтому, если дифференцировать по различным переменным ко­ординатам уравнения перемещений, после математи­ческих преобразований можно получить искомые зависимости между составляющими относительных линейных и угловых де­формаций. Так как эти зависимости связаны с условиями сплошности тел, они называются также уравнениями неразрыв­ности.

Если эти уравнения не соблюдены, то из малых параллелепи­педов и тетраэдров, на которые можно разделить упругое тело (рис. 14,а), после деформации каждого из них, зависящей от шести составляющих (рис. 14,б), может оказаться невозможным сло­жить непрерывное деформированное тело (рис. 14, в).

а	б	в

Рис. 14

Дифференцируя первые два уравнения (1.15) для линейных деформаций, находим

.

Складывая эти выражения и учитывая выражение для угло­вой деформации _ху, получаем

.

Произведя круговую подстановку индексов, можно получить еще два аналогичных уравнения, которые составят первую группу уравнений нера-зрывности

. (1.17,а)

Дифференцируем уравнения для угловых деформаций (1.15), складываем первые два уравнения и вычитаем третье:

.

Дифференцируем это уравнение по у:

.

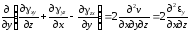После круговой подстановки можно получить еще два анало­гичных уравнения, которые составят вторую группу уравнений неразрывности

. (1.17,б)

Шесть условий (1.17,а) и (1.17,6) будут удовлетво­рены, если при решении задачи теории упругости удастся по заданным нагрузкам, действующим на тело, найти выражения для и, v и w. Если затем вычислить деформации по уравнениям (1.15), то урав­нения совместности, превратятся в тождества, так как они выведены из тех же уравнений (1.15).

Если же при решении задачи по нагрузкам найдем напря­жения, а затем деформации, необходимо проверить, удовлетво­ряют ли найденные деформации уравнениям совместности.

Можно доказать, что уравнения совместности представляют собой необходимые условия для того, чтобы по уравнениям (1.15) можно было найти составляющие перемещения по заданным составляющим деформациям.

Таким образом, зависимости (1.17,а и 17,б) являются необхо­димыми и достаточными условиями интегрируемости формул (1.15), обеспечивающими одновременно однозначность переме­щений. Это справедливо, если тело ограничено односвязной областью, т. е. областью, в пределах которой лю­бая замкнутая кривая может быть непрерывной деформацией стянута в точку без пересечения контура области.