1.5 Напряжения по октаэдрическим площадкам

Выделим у точки А площадками, равнонаклоненными к главным площадкам, элементарный октаэдр (рис. 10). При уменьшении размеров октаэдра его грани, лежащие в накрест расположенных четвертях, соль­ются, и мы получим четыре пло­щадки, проходящие через точку А, называемые октаэдрическими.

Рис. 10

Вычислим нормальные и каса­тельные напряжения, действую­щие по октаэдрической площадке. Так как в главных осях 1, 2, 3 все три направляющих косинуса нормали к октаэдрической пло­щадке одинаковы, а сумма их квадратов равна единице, то

(1.11)

Подставляя эти значения в формулу (1.6) и учитывая инвариантность суммы нормальных напряжений по трем взаимно перпендикулярным площадкам, находим нор­мальное напряжение по октаэдрической площадке

. (1.12)

Полное напряжение по октаэдрической площадке на осно­вании формул (1.1,a) и (1.4)

.

Касательное напряжение по октаэдрической площадке

.

Приведя подкоренное выражение к общему знаменателю, найдем

, (1.13)

или, с учетом выражения (1.10),

. (1.13,а)

1.6 Понятие о перемещениях. Зависимости между деформациями и перемещениями

Предположим, что упругое тело закреплено и не может перемещаться в пространстве. Тогда его точки могут изменять положение в пространстве только за счет деформации тела.

Пусть какая - нибудь точка А упругого тела (рис. 11), имевшая до де­формации координаты х, у и z, вследствие деформа­ции тела оказалась в

Рис. 11

поло­жении A₁ с координатами х + и, у + v и z + w. Отрезок AA₁ называется линейным перемещением точки A, а отрезки и, v и w — проекциями этого перемещения на оси координат. Переме­щения и их проекции для разных точек различны; они пред­ставляют собой непрерывные (по условиям сплошности) функции координат точки:

u =f₁ (x, y, z); v = f₂ (x, y, z); w = f₃ (x, y, z).

Деформированное состояние в точке А (рис. 12, а) будет известно, если будут известны деформации всех трех про­екций элементарного параллелепипеда. Для этого надо знать: относительные линейные деформации трех взаимно перпендикулярных ребер _x, _y и _z и изме­нения прямых углов между ребрами в плоскостях трех его граней, параллельных плоскостяx координат (относительные сдвиги или относительные угловые деформации _xy, _yz, _zx .

а	б

Рис. 12

Относительное изменение объема элементарного параллелепи­педа при деформации

Если отбросить величины второго и третьего порядка малости,

, (1.14)

где средняя относительная линейная деформация

.

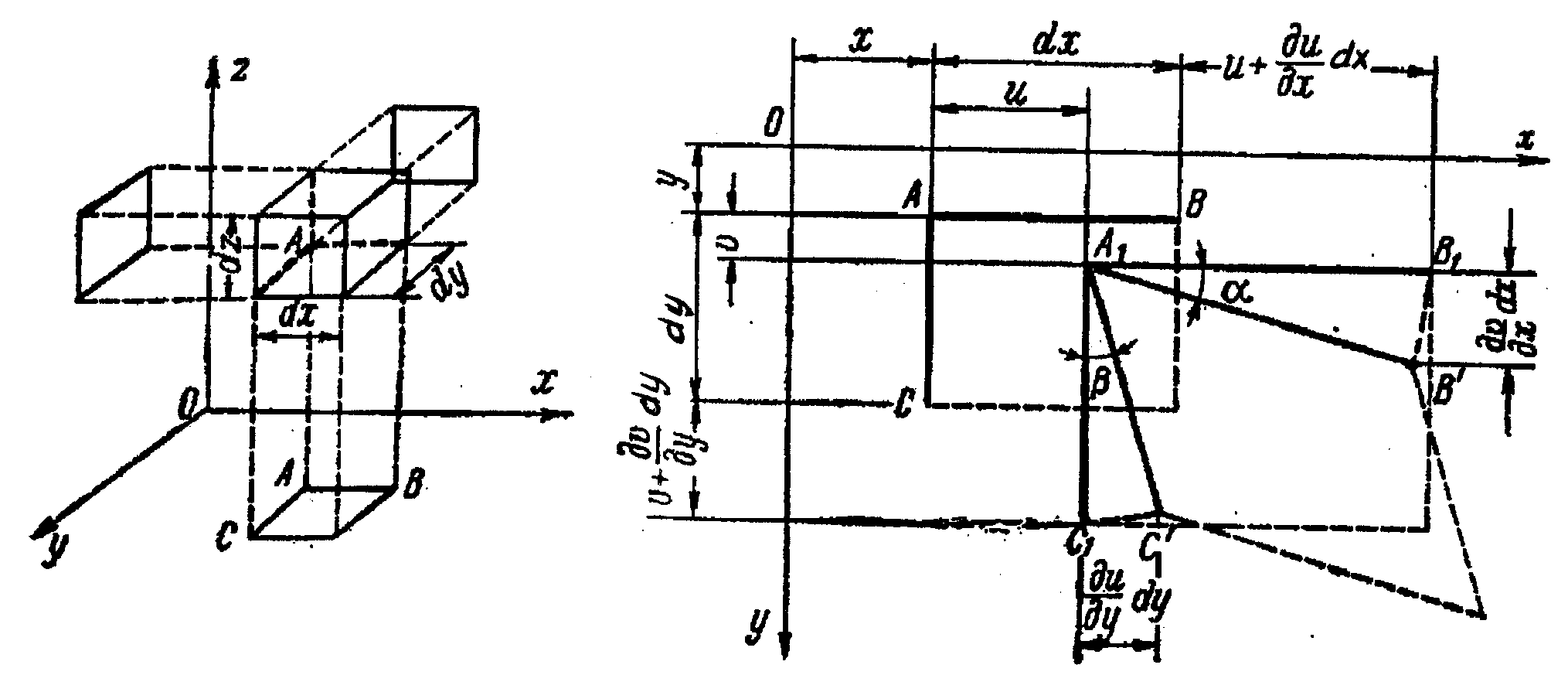
Найдем зависимости между составляющими деформациями и проекциями перемещения на оси координат. Для этого рассмотрим проекцию элементарного параллелепипеда на пло­скость хОу. Пусть заданы первоначальные координаты точки А — х и у и длины проекций ребер dx и dy (рис. 12, б). После дефор­мации тела точка А перейдет в положение A₁ , а точка В — в положение В₁.

Линейное перемещение точки В вдоль оси х равно сумме ли­нейного перемещения точки А и его приращения, вызванного изменением координаты х при переходе от точки А к точке В. Это приращение равно частному дифференциалу функции и = f₁ (x, y, z) по переменной х. Поэтому линейное перемещение точки В равно . Кроме того, вследствие изменения перво­начального прямого угла ВАС на величину точка В₁ займет положение В'. Отрезок В₁ В' представляет изменение пере­мещения v точки А при переходе от точки А к точке В вдоль оси х.

Относительная деформация _x ребра АВ

аналогично найдем

Изменение _xy прямого угла ВАС в плоскости хОу получим, заменив углы и их тангенсами,

Если пренебречь в скобках частными производными, которые малы по сравнению с единицей, то

Из проекций элементарного параллелепипеда на две другие плоскости координат найдем выражение для относительной линейной де­формации _z и относительных сдвигов _yz и _zx . В результате получим следующие шест зависимостей между относительными деформациями и перемеще­ниями:

. (1.15)

Зависимости (1.15) получены Коши. Исходя из гео­метрического смысла частных производных, стоящих в правой части, можно установить правила знаков: положительное значение относительных линейных деформаций соответствует удлинению, положительное значение отно­сительных сдвигов соответствует уменьшению прямых углов хОу, уОz и zОx.