5.11 Примеры

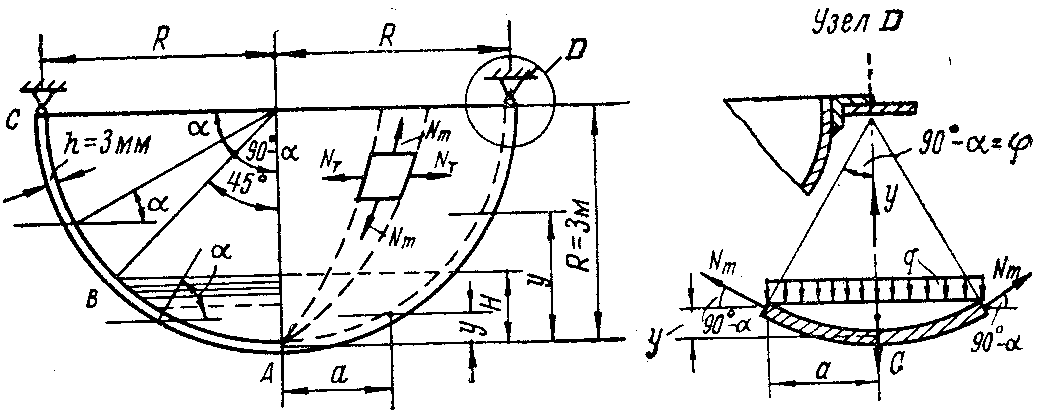
Пример 5.1. Тонкостенный сосуд, выполненный в виде полусферы, свободно закреплен по диаметральной окружности и частично нагружен, как показано на рис. 108,а, жидкостью с объемным весом  = 0,01 Мн/м³. Прене-брегая собственным весом сосуда, построить эпюры изменения главных напря­жений _m и _T в его стенке. Решение. Рассмотрим отдельно участок сосуда, испытывающий давление жидкости, и участок, не испытывающий этого давления.

1. 45 <  < 90° (участок ВА).

Из условия равновесия отсеченного от сосуда сегмента, показанного на рис. 108,б, по формуле (5.4) меридиональное погонное усилие

.

Вес жидкости G равен объему шарового сегмента высотой у, умноженному на объем­ный вес:

. (5.95)

Выразим радиус R через у и а. Из прямоугольного треугольника

откуда

.

а	б
в	г

Рис. 108

Подставим это выражение в формулу (5.95):

.

Учитывая, что , получим

.

Выразим через R и  интенсивность нагрузки q:

.

Подстановка найденных выражений для G и q в формулу (5.4) даст погонное меридиональное усилие

. (5.96)

Общий множитель, если R₁ = R₂ = R = 3 м,

.

Окружное погонное усилие N_Т находим из уравнения Лапласа (5.3):

или, подставляя вместо q его выражение,

. (5.97)

Таблица 5

, град	sin 	cos 	(1-cos )3	cos3 	0,25sin 	(1-sin )3 12cos2 	Nm R2	Nm103, Мн/м	Формула
0	-	1,000	-	1,000	-	-	-	3,54	(5.98)
30	-	0,870	-	0,755	-	-	-	4,08	(5.98)
45	0,705	0,705	0,0256	0,496	0,176	0,0040	0,080	7,20	(5.98); (5.96)
60	0,870	0,500	0,0022	0,250	0,217	0,0007	0,118	10,62	(5.96)
90	1,000	0	0	0	0,250	0	0,150	13,50	(5.96)

2. 0 <  < 45⁰ (участок СВ).

Высота жидкости в сосуде

Вес G жидкости в сосуде

.

Таблица 6

, град	Nm103, Мн/м	sin   0,707	R2(sin    0,707)  103, Мн/м	NT103, Мн/м	Формула
0	3,54	-	-	3,54	(5.99)
30	4,68	-	-	4,68	(5.99)
45	7,20	0	0	7,20	(5.99); (5.97)
60	10,62	0,165	14,85	+4,23	(5.97)
90	13,50	0,295	26,55	+13,05	(5.97)

Погонное меридиональное усилие

. (5.98)

Погонное окружное усилие N_T найдем из уравнения Лапласа:

. (5.99)

Оно равно по величине и противоположно по знаку меридианальному.

Результаты подсчета погоных усилий представлены в табл. 5 и 6. По данным этих таблиц построены эпюры усилий N_m и N_T (рис. 108,в, г).

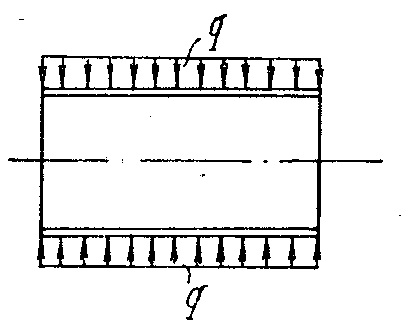
Пример 5.2. Цилиндрический сталь­ной корпус, имеющий подкрепляющие кольца и торцы (рис. 109), подвержен внутреннему давлению q = 2 Мн/м². Построить эпюры мери­диональных изгибающих моментов М_х вблизи от подкрепляющих колец в двух предполо­жениях: 1) кольца абсолютно жесткие; 2) кольца упругие. Модуль упругости Е= 2  10⁵ Мн/м²;  = 0,3.

Рис. 109

Решение. 1. Вычисление вспомогательных величин.

Цилиндрическая жесткость

.

Коэффициент затухания

.

Длина оболочки, при которой ее можно считать длинной,

Так как l = 0,6 > 0,266 м, можно не учитывать совместное влияния двух подкрепляющих колец на расположенную между ними оболочку и вести расчет по формулам для длинной оболочки. В формулы, выведенные для цилин­дрической оболочки, подверженной наружной нагрузке интенсивностью q, нужно интенсивность подставлять со знаком минус.

2. Определим изгибающие моменты М_х в предположении, что кольца абсолютно жесткие.

Сила взаимодействия между кольцами и оболочкой по формуле (5.70)

.

Погонная поперечная сила Q на оси кольца

.

Погонный изгибающий момент М₀ на оси кольца

.

Ординаты эпюры погонных изгибающих моментов

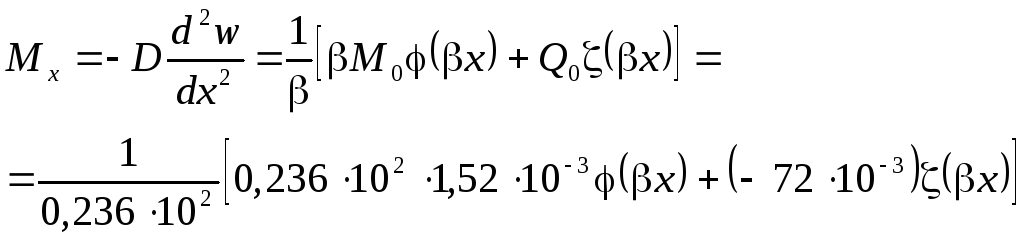
или после упрощения

.

Функции и берутся из табл. 4. В табл. 7 представлены результаты вычислений ординат М_х. По данным таблицы построена эпюра на рис. 110.

Таблица 7

№ точки	х	х, см	(х)	(х)	1,52(х), Мн	3,05(х), Мн	Мх103, Мн
0	0	0	1,0000	0	1,520	0	1,520
1	0,2	0,85	0,9651	0,1627	1,464	0,495	0,966
2	0,4	1,65	0,8784	0,2610	1,332	0,795	0,537
3	0,6	2,54	0,7628	0,3099	1,160	0,945	0,215
4	0,8	3,40	0,6354	0,3223	0,965	0,982	0,017
5	1,0	4,25	0,5083	0,3095	0,775	0,945	0,170
6	1,5	6,34	0,2384	0,2226	0,363	0,680	0,317
7	2,0	8,50	0,0667	0,1230	0,101	0,375	0,274
8	2,5	10,6	0,0166	0,0492	0,025	0,160	0,175
9	3,0	12,7	0,0423	0,0071	0,064	0,022	0,086
10	4,0	16,9	0,0258	0,0139	0,039	0,042	+0,003
11	5,0	21,2	0,0046	0,0065	0,007	0,0020	+0,013

Положение нулевых точек эпюры изгибающих моментов (см. рис. 110) опре­деляется расстоянием

После второй нулевой точки, на расстоянии 3,33 + 13,33 = 16,66 см от оси кольца, изгибающие моменты уменьшаются до величины

Рис. 110

и вызывают напряжение

Это напряжение настолько мало, что его можно не учитывать.

2. Определяем изгибающие моменты М_х в предположении, что кольца упругие. Моменты М_х пропорциональны краевому изгибающему моменту М₀ и краевой поперечной силе Q₀, которые, в свою очередь, пропорциональны силе взаимодействия Х. Поэтому ординаты эпюры М_х получаются путем умножения ординат эпюры M_х, вычисленных в табл. 7, на коэффициент

Таким образом, при учете податливости колец погонные изгибающие моменты составляют лишь 43% от моментов, вычисленных в предположении жестких ко­лец. Соответствующая эпюра изгибающих моментов М_х построена на рис. 110 штриховой линией.

Пример 5.3 Для оболочки, рассмотренной в предыдущем примере, построить эпюры погонных изгибающих моментов М_х и погонных поперечных сил Q_x в месте примыкания оболочки к плоскому торцу, возника­ющих от внутреннего давления q = 50 н/см², вычислить главные напряжения _x и _y и составить условие прочности по третьей теории прочности. Допускаемое напряжение [] = 40 000 н/см².

Решение. По табличным формулам находим значения погонных краевых изгибающих моментов М₀ и поперечных сил Q₀ для случая примыкания цилин­дрической оболочки к плоскому торцу, приняв следующие исходные данные:

 геометрические размеры

h₁ = h₂ = h = 1 cм; R = 30 см;

 упругие постоянные Е = 2  10⁷ н/см²;  = 0,3;

D₁ = D₂ = D = 1,83  10⁶ нсм;

 интенсивность радиальной нагрузки

q = 50 н/cм²;

 коэффициент затухания перемещений

₁ = ₂ =  = 0,236 1/см.

Погонный изгибающий момент в сечении оболочки, примыкающем к торцу, вычисляется по формуле(5.85):

Погонная поперечная сила в этом сечении вычисляется по формуле (5.84)

Зная М₀ и Q₀, можно вычислить погонные изгибающие моменты М_х и погонные поперечные силы Q_х вдоль обра­зующей х:

Функции  (x),  (х) и  (х) берутся из табл. 4. В табл. 7 представлены результаты вычислений ординат изгибающих моментов М_х и поперечных сил Q_х. По данным таблицы построены эпюры на рис. 111. Положение нулевых точек эпюры Q_х опре­деляется расстояниями (х₀)₁ = 1,25 см и (х₀)₂ = 14,8 см. В этих сечениях изги­бающие моменты достигают максимума.

Таблица 8

№ точки	х	х, см	(х)	(х)	(х)	5170(х)	1258(х)	5325(х)	2440(х)	Мх, нсм/см	Qx, н/см
1	2	3	4	5	6	7	8	9	10	11	12
0	0	0	1,000	0	1,000	5170	1258	0	0	5170	1258
1	0,2	0,85	0,9653	0,1627	0,6398	5000	802	870	480	5870	322
2	0,4	1,65	0,8784	0,2610	0,3564	4537	448	1390	770	5927	322
3	0,6	2,54	0,7628	0,3099	0,1431	3940	180	1650	912	5590	732
4	0,8	3,40	0,6354	0,3223	0,0093	3284	12	1720	952	5004	964
5	1,0	4,25	0,5083	0,3096	0,1108	2625	136	1650	915	4275	1051
1	2	3	4	5	6	7	8	9	10	11	12
6	1,5	6,34	0,2384	0,2226	-0,2068	1237	260	1188	657	2425	917
7	2,0	8,5	0,0667	0,1230	-0,1794	345	226	655	362	1000	588
8	2,5	10,6	0,0166	0,0492	-0,1149	86	144	262	145	176	289
9	3,0	12,7	0,0423	0,0071	--0,0563	218	70	37	21	181	91
10	4,0	16,9	0,0258	0,0139	0,0019	134	2	74	41	208	43
11	5,0	21,2	0,0046	0,0065	0,0084	24	10	34	19	58	29

Рис. 111

Изгибающий момент в плоском днище вычисляется как для круглой пла­стины, нагруженной по контуру погонными радиальными моментами. Эти мо­менты постоянны по диаметру торца и вызывают шаровой изгиб. Кроме того, на торец действует равномерно распределенная нагрузка интенсивностью q. Она вызывает изгибающие моменты M_r, показанные на рис. 112.

В центре днища от нагрузки q

Эпюру радиальных изгибающих моментов строим по принципу независи­мости действия сил как суммарную эпюру моментов, возникающих под действием моментов М₀ и нагрузки q.

Рис. 112

Наиболее напряженная точка нахо­дится на расстоянии (х₀)₁=1,25 см от места примыкания цилиндрической обо­лочки к торцу. В этом месте действуют погонные усилия:

M_y = M_x = 0,3  5950 = 1780 (н см)/см;

Для определения четвертого члена в формуле (5.94) для экваториального (окружного) нормального напряжения _у необходимо вычислить радиальное пере­мещение w_x в сечении, в котором про­изводится вычисление напряжений:

Наибольшие главные нормальные напряжения:

 меридиональное, действующее вдоль образующей, по формуле (5.93)

 экваториальное, действующее вдоль окружности, поперечного сечения, по формуле (5.94)

Условие прочности по третьей теории прочности при ₃ = 0:

Пример 5.4. Для цилиндрической оболочки, нагруженной радиальной равномерно распределенной нагрузкой интенсивностью q = 30 н/см и защем­ленной концами (рис. 113,а), вычислить ординаты перемещений w_x по радиусу и построить изогнутую срединную поверхность. Материал – титан. Модуль упру­гости Е= 1,1  10⁷; коэффициент Пуассона  = 0,3.

Решение. Цилиндрическая жесткость

Коэффициент затухания перемещений

Отношение

следовательно, оболочка длинная.

Перемещения w находим наложением решений для незащемленной обо­лочки, нагруженной радиальным давлением q (рис. 113,в), и для оболочки, на­груженной усилиями М₀ и Q₀ на торцах (рис. 113,б).

а	б
	в

Рис. 113

Условие совместности деформации

Условие защемления  равенство нулю угла наклона касательной к оболочке в защемлении:

Эти два условия такие же, как для оболочки, подкрепленной абсолютно жесткими кольцами. Поэтому выражения для изгибающего момента М₀ и поперечной силы Q₀ в защемлении те же, что и для подкрепленной оболочки:

Зная эти усилия, перемещения в любой точке можно вычислить по формуле

Первый член в этой формуле вычисляется согласно (5.48), а второй

Характер изогнутой средней поверхности показан на рис. 113.

181