Уравнения (5.82) и (5.83) содержат две неизвестные величины: М0 и Q0. Решая систему, находим погонную поперечную силу и изгибающий момент в сопряжении оболочки с плоским торцом
![]() ;
(5.84)
;
(5.84)
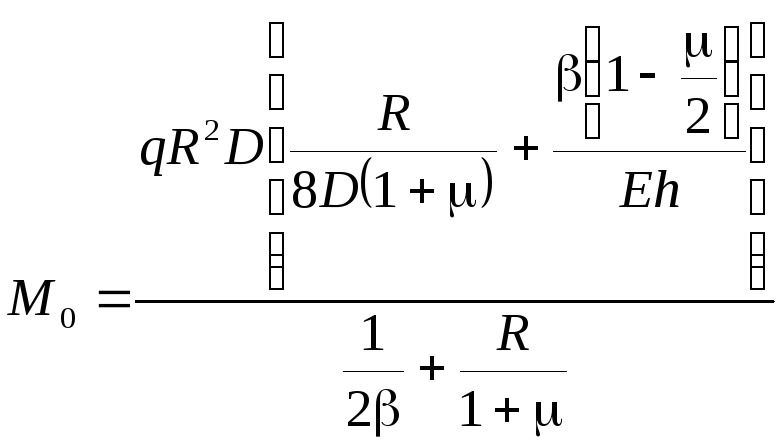 .
(5.85)
.
(5.85)
Пользуясь выражениями радиальных смещений w и углов поворота сечений оболочек и уравнениями (5.76) и (5.77) совместности деформаций, можно аналогичным путем вывести формулы для погонных поперечных сил Q0 и погонных изгибающих моментов М0 , возникающих в сопряжении цилиндрической оболочки с торцевой, имеющей форму полусферы, шарового сегмента, конуса или плоской пластины, при различных толщинах оболочки в цилиндрической и торцевой частях. Зная Q0 и М0, можно вычислить wx, Qx и Мх в любой точке цилиндрической части, пользуясь формулами (5.33), (5.55), (5.56).
5.8 Определение перемещении и усилий в короткой цилиндрической оболочке
Выше (расчетный
случай 2) указывалось, что когда расстояние
l
между торцами или подкрепляющими
кольцами цилиндрической оболочки
меньше отношения
![]() ,
усилия и перемещения в оболочке следует
определять, учитывая ее ограниченную
длину. В этом случае удобнее пользоваться
для интеграла дифференциального
уравнения равновесия элемента (5.32)
формулой (5.34),
а не (5.33),
а начало координат располагать в середине
длины оболочки.
,
усилия и перемещения в оболочке следует
определять, учитывая ее ограниченную
длину. В этом случае удобнее пользоваться
для интеграла дифференциального
уравнения равновесия элемента (5.32)
формулой (5.34),
а не (5.33),
а начало координат располагать в середине
длины оболочки.
Кроме того, для определения произвольных постоянных интегрирования должны быть составлены другие граничные условия. Например, первое условие для расчетного случая 1, составленное в предположении равенства нулю радиального перемещения w при абсциссе х, стремящейся к бесконечности, не может быть использован для короткой оболочки, но имеется возможность использовать граничные условия на обоих торцах оболочки.
Для примера составим уравнение изогнутой срединной поверхности для нагрузки Q0 и M0 (см. расчетный случай 1), приложенной к короткой оболочке (рис. 105). Так как интенсивность нагрузки q = 0, уравнение изогнутой срединной поверхности в соответствии с формулой (5.34)
![]()

Рис. 105
Постоянные A определяем из следующих граничных условий:
![]()
Так как каждое из
последних двух условий объединяет в
себе два условия (плюс или минус
![]() ),
число уравнений, необходимых для
определения постоянных А,
достаточно. Усилия и перемещения в
коротких оболочках удобно выражать с
помощью тригонометрических и
гиперболических функций от
),
число уравнений, необходимых для
определения постоянных А,
достаточно. Усилия и перемещения в
коротких оболочках удобно выражать с
помощью тригонометрических и
гиперболических функций от
![]() .
.
5.9 Температурные напряжения в цилиндрической оболочке
-
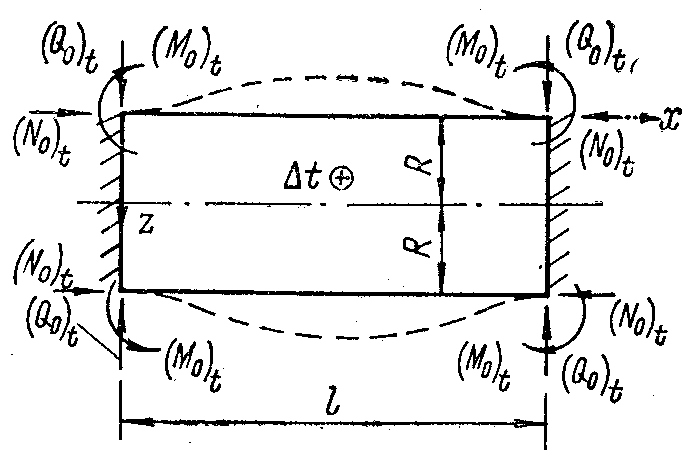
Одинаковое постоянное изменение температуры во всех направлениях. Если торцы оболочки свободны и деформация ее как в радиальном направлении, так и вдоль образующей не стеснена, напряжения при равномерном изменении температуры не возникают. При любом способе симметричного закрепления торов (рис. 106) в торцевом сечении возникают те или иные реактивные погонные усилия: изгибающие моменты (M0)t, продольные (N0)t и поперечные (Q0)t силы.
|
а |
б |
|
|
|
Рис. 106
Для нахождения
изгибающих моментов
и поперечных
сил,
возникающих
при изменении температуры на
![]() ,
приравняем радиальные температурные
перемещения,
равные абсолютному изменению длины
радиуса,
,
приравняем радиальные температурные
перемещения,
равные абсолютному изменению длины
радиуса,
![]()
радиальным перемещеням wx=0 в сечении х = 0, вызванным погонными моментами (M0)t и поперечными силами (Q0)t [см. формулу (5.57)]. Получим уравнение
![]() ,
(5.86)
,
(5.86)
содержащее два
неизвестных:
![]() .
.
Второе уравнение, содержащее эти два неизвестных, получится из условия равенства нулю угла наклона касательной к оси х в защемлении (рис. 106,а) или в середине пролета (рис. 106,б). Для защемленной оболочки (рис. 106,a) это условие запишется по формуле (5.58)
![]()
![]() ,
(5.87)
,
(5.87)
для опертой оболочки (рис. 106,б) по формуле (5.54)
![]() . (5.88)
. (5.88)
Решая совместно уравнения (5.86) и (5.87) или (5.86) и (5.88), можно найти усилия (M0)t и (Q0)t, а затем w, Qx и Мx в любом сечении с помощью формул (5.53), (5.55) и (5.56).
Погонная продольная сила (Nx)t, возникающая при закреплении торцов оболочки, определяется из условия совместности деформации вдоль оси х
![]()
откуда
![]() .
.
-
Постоянная разность температур в радиальном направлении. Обозначим через t1 температуру на внутренней поверхности оболочки и через t2 на наружной. В сечениях, удаленных от закрепленных торцов, или в случае, если торцы свободны, местного изгиба нет. Предположим, что температура и вызванные ею относительные линейные деформации изменяются по толщине h оболочки по линейному закону (рис. 107). Примем t2 > t1 и обозначим
![]() .
.
Относительная температурная деформация наружного волокна оболочки
![]() .
.

Рис. 107
С другой стороны, эта же деформация, на основании гипотезы плоских сечений
![]() ,
,
где 1 радиус образующих цилиндра при изгибе.
Приравняв эти выражения друг другу, получим кривизну
![]() .
(5.89)
.
(5.89)
В то же время искривление образующей цилиндрической оболочки под действием изгибающего погонного момента Мх характеризуется кривизной [см. формулу (5.26)]
![]() .
(5.90)
.
(5.90)
Если торец защемлен, искривления образующей не происходит, погонный изгибающий момент Мх находим, приравнивая выражения (5.89) и (5.90):
![]()
Наибольшие нормальные напряжения в крайних волокнах
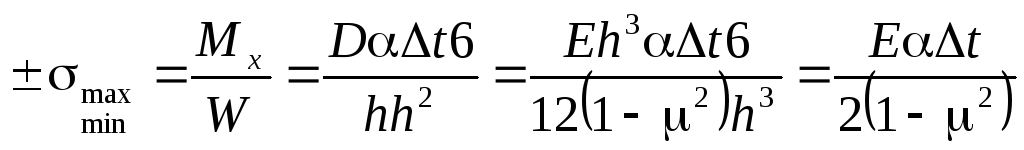 .
(5.91)
.
(5.91)
В случае
t2
> t1
знак плюс соответствует наружной
поверхности оболочки, знак минус
внутренней. Около закрепленных
торцов
возникает местный изгиб, и на напряжение
по формуле (5.91) алгебраически накладываются
напряжения, вычисленные
по значению,
![]() из условия удовлетворения граничным
условиям.
из условия удовлетворения граничным
условиям.
3. Постоянная разность температур в направлении оси х. Изменение температуры вдоль оси х вызывает изгиб оболочки, обусловленный различными радиальными перемещениями поперечных сечений. Он может описываться дифференциальным уравнением, аналогичным уравнению(5.32), если подставить в него переменную интенсивность q, вызывающую такие же деформации, как и переменная температура.
Примем закон изменения температуры по длине оболочки
![]()
Относительное окружное напряжение по закону Гука
![]()
а погонная продольная сила
![]() .
.
С другой стороны, Nу = —qR (см. рис. 101), откуда интенсивность радиальной нагрузки, эквивалентной температурному воздействию,
![]() .
.
Подстановка этого значения в уравнение (5.32) дает
![]() (5.92)
(5.92)
и задача сводится к интегрированию дифференциального уравнения (5.92).