5.7 Местные напряжения в сопряжении оболочек

Уравнение совместности деформации. При действии на обо­лочку равномерно распределенного давления в местах нарушения непрерывности меридионального сечения возникают местные уси­лия изгибающие моменты и поперечные силы. Например, обо­лочка, показанная на рис. 102 состоящая из

q

рис. 102

цилиндрической части Ц и торцевой части Т в виде шарового сегмента, не имеет общей касательной в месте сопряжения этих частей. Поэтому по окружности СС их соприкосновения возникнут погонные уси­лия Q₀ и М₀ . Объясняется это тем, что линейные перемещения w и углы поворота касательных к изогнутой срединной поверхно­сти, возникающие под действием равномерно распределенной нагрузки q, в общем случае различны для цилиндрической и тор­цевой частей оболочки. Для цилиндрической радиальные перемещения обычно больше, чем для торцевой, а угловые равны нулю. У торцевой части могут возникнуть угловые перемещения по окружности СС. Поэтому, если мысленно отделить торцевую часть от цилиндрической по

Рис. 103

сечению С С (рис. 103), в сечении возникнут линейный разрыв

(5.74)

и угловой разрыв

, (5.75)

где и радиальные перемещения цилиндрической и торцовой частей от нагрузки q;

угловое перемещение торцевой части от нагрузки q.

Для уничтожения этих разрывов по сечению С С необходимо приложить погонные поперечные силы Q₀ и изгибающие мо­менты М₀ . Эти усилия вызовут в сечении следующие смещения: погонная поперечная сила Q₀ линейные смещения и и угловые смещения и погонный изгибаю­щий момент M₀ линейные смещения и и угловые смещения и 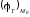В общем случае эти смещения различны для торцевой и цилиндрической частей. Алгебраическая сумма линейных смещений должна равняться линейному разрыву , а алгебраическая сумма угловых смещений угловому разрыву

Таким образом, можно записать уравнения совместности дефор­маций (рис. 104)

(5.76)

. (5.77)

а б

Рис. 104

Эти уравнения показывают, что возникающие в сечении С С в непрерывной оболочке погонные усилия Q₀ и М₀ уничтожают линейный и угловой разрывы и и заставляют торцы цилиндри­ческой и торцевой оболочек совпадать в переломе.

Приведенные рассуждения и уравнения (5.76) и (5.77) справедливы для сопряжения двух оболочек любого очертания и, в частности, для сопряжения цилиндрической оболочки с торце­вой частью любого осесимметричного очертания шарового, конического или плоского.

Сопряжение цилиндрической оболочки с полусферическим дни­щем. Определим усилия Q₀ и М₀ для наиболее простого сопря­жения цилиндрической оболочки с торцом в виде полусферы. В случае одинаковой толщины h цилиндрической и сферической частей можно считать, что по сечению С С общая касательная для этих частей поворачивается в их сопряжении под действием усилий Q₀ на одинаковый угол и взаимный угол поворота отсут­ствует. Значит, в сечении С С не возникает погонного изгибаю­щего момента, т. е. М₀ = 0.

Остается только погонная поперечная сила Q₀, которую можно найти из решения геометрического уравнения (5.74), положив в нем члены, зависящие от М₀, равными нулю. Подставив в урав­нение (5.74) абсолютные значения по формуле (5.10) и , найдем

. (5.78)

Приняв во внимание, что изгиб около сечения С С местный и достигает значительной величины как в цилиндрической, так и в сферической оболочке лишь вблизи от места сопряжения, условно заменим сферическую оболочку цилиндрической. В таком случае, подставив в уравнение (5.76) абсолютные значения по формуле (5.57) (расчетный случай 1) при M₀ = 0 и по формуле (5.78), найдем

,

откуда

, (5.79)

или, подставив в формулу (5.79) значение ³ по формуле (5.69)

Таким образом, в случае сопряжения цилиндрической и полу­сферической оболочек одинаковой толщины, нагруженных ра­диальной сжимающей нагрузкой интенсивностью q, можно при­нять

Сопряжение цилиндрической оболочки с плоским днищем. Оболочка нагружена внутренним радиальным давлением q. Пло­ское днище рассматривается как круглая пластина с радиусом R, нагруженная равномерным поперечным давлением q и погонным моментом М₀ по кромке. Ось х направлена по радиусу пластины.

Уравнение (5.60) углов поворота пластины

, (5.80)

где D₁ цилиндрическая жесткость пластины.

В центре пластины при х = 0, угол наклона касательной пло­скости равен нулю, поэтому первое граничное условие = 0 при х = 0, откуда С₂ = 0.

Выражение для радиального погонного изгибающего мо­мента

.

На контуре пластины

.

Этот погонный момент должен равняться и быть противополож­ным по знаку погонному моменту M₀, действующему по кромке оболочки, поэтому второе граничное условие (M_r)_x=R = M₀, откуда

. (5.81)

Подстановка значения С₂ = 0 и C₁ по формуле (5.81) в уравне­ние (5.80) даст следующее значение для угла поворота на контуре пластины:

.

Радиальный изгибающий момент в произвольном сечении пластины на расстоянии х от центра

.

Если считать радиальное перемещение пластины пренебрежимо малым в уравнении совместности (5.76), можно принять . Тогда оно примет вид

.

Учитывая, что

,

получим

или, после подстановки радиальных перемещений w_Ц ,

, (5.82)

где D — цилиндрическая жесткость оболочки.

Уравнение (5.77) примет вид:

. (5.83)

40