8.4.5.2. Критерій домінуючого результату

Коли F = F, то згідно з критерієм домінуючого результату оптимальне рішення забезпечується максимаксною (maxmax) стратегією:

.

У випадку, коли оптимальне рішення забезпечується мінмінною (minmin) стратегією:

.

Доцільність самостійного використання цього критерію при прийнятті рішень є досить проблематичною. В основному він використовується як складова частина при побудові складних моделей прийняття багатоцільових рішень для імітації найсприятливіших ситуацій (наприклад, в критерії Гурвіца, що буде розглядатися під час аналізу шостої ІС), а також під час побудови ієрархічних моделей, які розглядатимуться під час вивчення наступної теми (теми 9).

8.4.5.3. Критерій мінімального ризику Севіджа

Цей критерій був запропонований у 1951 році і є одним з основних критеріїв, що відповідає принципові мінімаксу. Початковим моментом для використання критерію Севіджа є перехід від функціоналу оцінювання F до матриці ризику R. Тоді згідно з Севіджем оптимальним слід вважати рішення:

.

Приклад 8.15. Виходячи з умови задачі про фруктового дилера (приклад 8.2), знайти мінімальний рівень збитків, пов’язаних з невикористанням своїх можливостей, а також стратегію, що його гарантує.

_! Вказівка. Перейшовши до матриці невикористаних можливостей, скористатись критерієм Севіджа.

Відповідь. Стратегія х₂ (5 кошиків) або х₃ (6 кошиків)._-

8.4.6. Шоста інформаційна ситуація ( i6 )

Ця ситуація характеризується наявністю чинників, що зумовлюють «проміжну» між I₁, I₂ , I₃ , I₄ та I₅ поведінку ЕС.

Класичними прикладами критеріїв прийняття компромісних рішень в полі I₆ є критерій Гурвіца, модифіковані критерії та критерій Ходжеса-Лемана [1, 2, 3]. Критерій Гурвіца та модифіковані критерії використовуються для прийняття компромісного рішення в полі однієї інформаційної ситуації, критерій Ходжеса-Лемана — в полях двох різних інформаційних ситуацій.

Згадані вище критерії прийняття рішень (в полі І₆) можна розглядати як часткові випадки загальної ієрархічної моделі прийняття багатоцільових та багатокритеріальних рішень, яка становить предмет досліджень розділу 9.

8.4.6.1. Критерій Гурвіца

Критерії Вальда та Севіджа песимістичні в тому сенсі, що з кожним рішенням вони поєднують стан середовища, яке приводить до гарантованих (безризикових) наслідків для прийнятого суб’єктом керування рішення. Для моделювання поведінки середовища, що вважається найкращим для суб’єкта керування, Гурвіц [2,3] запропонував використовувати зважену комбінацію найкращого та найгіршого.

Такий підхід до вибору рішень відомий як критерій показника песимізму-оптимізму. Особливістю цього критерію є те, що в ньому передбачається не повний антагонізм середовища, а лише частковий.

Згідно з критерієм Гурвіца у випадку, коли F = F⁺, оптимальним є рішення

де

Величину називають -показником Гурвіца для рішення х_kX. Вважають, що рішення х_k буде пріоритетнішим (придатнішим), ніж (х_k ) тоді і тільки тоді, коли G⁺(; ) > G⁺(; ).

Відзначимо, що при  = 1 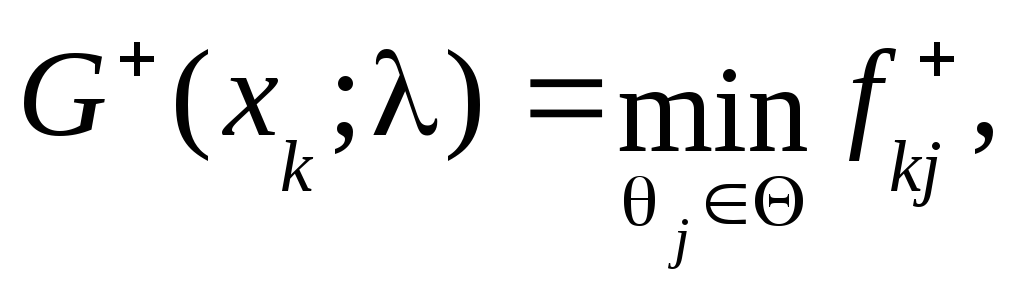тобто критерій Гурвіца збігається з критерієм Вальда, а при  = 0 тобто критерій Гурвіца збігається з максимаксним критерієм. У першому з цих випадків вважається, що середовище максимально протидіє цілям суб’єкта управління, в другому, навпаки, середовище найкращим чином допомагає цілям управління. В першому з цих випадків ( = 1) поведінка ЕС порівнюється з «розумним» суперником, у другому випадку ( = 0) — із «зовсім бездарним» суперником. Однак, якщо вважати, що ці випадки є крайніми, то істинна поведінка середовища буде проміжною і характеризуватиметься величиною   (0; 1).

У випадку, коли , оптимальним є рішення

де

У цьому випадку тоді і тільки тоді, коли . Як і раніше, параметр  можна інтерпретувати як коефіцієнт несхильності до ризику.

Якщо для кожного рішення x_k  X вводиться свій показник _k  (0,1), то має місце модифікований критерій Гурвіца. Тоді замість G⁺(x_k; ) вводиться _k-показник Гурвіца:

Аналогічно визначається і величина .

Щодо вибору коефіцієнта   [0; 1], то чіткої методики його обрання немає, але можна запропонувати кілька рекомендацій.

При виборі коефіцієнта  суб’єктом управління можуть бути використані евристичні методи, пов’язані з його досвідом та знанням особливостей обрання середовищем своїх станів з множини .

Наприклад, чим більш сильні чи переконливі докази про прийняття однієї з крайніх поведінок середовища, тим ближче буде  до одиниці або нуля. Для значення  = 1/2 цілком природно вважати, що суб’єкт управління вважає середовище однаковою мірою як антагоністичним, так і максимально «допомагаючим» цілям управління.

Якщо суб’єкт управління знає щільність розподілу () параметра ,   [0; 1], то для оцінки цього параметра можна використати його середнє значення, що обчислюється за формулою:

Можна також знаходити оцінку параметра шляхом обчислення математичного сподівання -показника Гурвіца:

У загальному випадку оптимальне рішення за критерієм Гурвіца є функцією від . Вибір параметра  можна здійснити також з позицій функції схильності-несхильності до ризику суб’єкта керування. Нехай F = F⁺. Для рішення х_k, k = 1, ..., m, покладемо Значення відкладемо на осі абсцис. Тоді можуть виникнути такі ситуації:

1) якщо , будуть належати до зони схильності до ризику, то покладаємо _k = 0;

2) якщо , будуть належати до зони несхильності до ризику, то _k = 1;

3) якщо ж інтервалу для всіх k = 1, ..., m, належить зона нейтральності до ризику і f⁰ одна з точок цієї зони (наприклад, f⁰ — це крайня ліва точка зони нейтральності), то

Всі інші ситуації, що є проміжними по відношенню до розглянутих вище, вписуються у наведену схему. Слід мати на увазі, що ситуацію, коли інтервал повністю належить до зони нейтральності (чи співпадає з нею), слід вважати випадком невизначеності щодо вибору параметра , тобто в цій ситуації параметру  можна надати будь-яке значення з інтервалу [0;1].

Приклад 8.16. Вивчаються щодо інвестування чотири різних портфелі цінних паперів. Розрахункові норми прибутків залежно від стану економіки (₁ — піднесення, ₂ — стагнація, ₃ — рецесія) наведено в таблиці 8.2.

Таблиця 8.2

Варіанти портфелів цінних паперів	Норми прибутку (%)
	1	2	3
х1 х2 х3 х4	20 75 25 80	30 20 80 50	15 35 25 45

Функція корисності інвестора



Необхідно вибрати портфель цінних паперів, який був би оптимальним з точки зору критерію Гурвіца.

Розв’язання. Оскільки у функції корисності чітко не виділена її лінійна частина, то зону нейтральності до ризику буде характеризувати точка її перегину. Точку перегину знаходимо з рівняння:

На основі таблиці 8.2 формуємо матрицю F ⁺:

.

Визначимо тепер коефіцієнти несхильності до ризику для кожного рішення. Оскільки для першого рядка матриці F ⁺ (для рішення х₁)

max(20; 30; 15) = 30 < 40 = t_o , то ₁ = 0.

Для рішення х₂ :

Для рішення х₃:

Оскільки для четвертого рядка матриці F ⁺

min(70; 50; 45) = 45 > 40 = t_o, то ₄ = 1.

Скориставшись тепер операцією згортання Гурвіца (операцією переходу від матриці F⁺ до відповідних -оцінок Гурвіца G⁺(x_k; _k)), отримуємо:

Оскільки згідно з критерієм Гурвіца (у випадку, коли F = F ⁺) оптимальному рішенню відповідає максимальний елемент стовпчи­ка G ⁺, то таким рішенням є х₄._-

Приклад 8.17. Скористаємося умовою прикладу 8.16. Але, на відміну від нього, функцію корисності вважатимемо невідомою. Несхильність до ризику інвестора виражається тим, що обраний ним коефіцієнт несхильності до ризику  є [0,6; 0,8]. Необхідно обрати варіант рішення, який був би оптимальним:

а) з точки зору накладених умов;



б) з урахуванням матриці ризику (невикористаних можливостей).

Розв’язання. а) Оскільки функціонал оцінювання містить позитивний інгредієнт, то -оцінки Гурвіца обчислюються за формулою:

.

Якщо до матриці F ⁺ застосувати операцію згортання Гурвіца з довільним параметром , то отримуємо:

У системі координат (; y) побудуємо ламану Гурвіца [2,3] (рис. 8.2).

Рис. 8.2. Визначення оптимального рішення за допомогою ламаної Гурвіца (F = F⁺)

Згідно з означенням ламана Гурвіца задається співвідношенням

,

а тому на рис. 8.2 її графічним відображенням є ламана лінія АВС. Оскільки лінії G⁺(x₁;) та G⁺(x₂;) лежать під ламаною АВС, то рішення х₁ та х₂ до уваги можна не приймати. При є[0;₀] більших значень набирає функція G⁺(x₃;), а тому для цих значень параметра  розв’язок x₃ є більш пріоритетним, ніж х₄. При є[₀;1] величина G⁺(x₄;)>G⁺(x₃;), тобто для цих значень  пріоритет­нішим є розв’язок х₄. Значення ₀ знаходимо з умови: G⁺(x₄; ) = G⁺(x₃; )  (1 – ₀)80 + ₀ 25 = (1 – ₀)70 + ₀ 45  ₀ = 1/3.

Оскільки згідно з умовою несхильність до ризику інвестора адекватна тому, що є[0,6; 0,8], то, як це видно з рис.8.2, оптимальним слід вважати рішення х₄.

б) Від заданого функціонала оцінювання F ⁺ перейдемо до матриці ризику:

.

Оскільки матриця має негативний інгредієнт, то для неї -оцінки Гурвіца обчислюються за формулою:

.

А тому, якщо до матриці застосувати операцію згортання , то отримуємо:

На рис. 8.3 побудована відповідна ламана Гурвіца.

У випадку, коли функціонал оцінювання містить негативний інгредієнт (в даному випадку роль функціонала оцінювання відіграє матриця ), ламана Гурвіца задається співвідношенням:

а тому на рис. 8.3 її графічним відображенням є відрізок ОА прямої лінії.

Рис. 8.3. Визначення оптимального рішення за допомогою ламаної Гурвіца

Як бачимо, виходячи з позицій найкращого використання своїх можливостей, найвищий пріоритет має рішення х₄._-