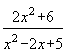Задание №5
Тема. Интерполяционный многочлен.
Задание: Для заданной функции y=f(x) на [a, b] построить интерполяционный многочлен Лагранжа Ln(x) (n=5) и интерполяционный многочлен Ньютона Pn(x) (n=7) для равноотстоящих узлов. Построить графики функции и многочленов.
Варианты индивидуальных заданий
Номер варианта |
f(x) |
a |
b |
Номер варианта |
f(x) |
a |
b |
1 |
|
2 |
5 |
16 |
|
2 |
5 |
2 |
|
-9 |
9 |
17 |
|
-2 |
2 |
3 |
|
-2 |
2 |
18 |
|
-3 |
3 |
4 |
|
-1 |
5 |
19 |
|
2 |
5 |
5 |
|
-5 |
3 |
20 |
|
-3 |
3 |
6 |
|
1 |
3 |
21 |
|
-1 |
4 |
7 |
|
0 |
4 |
22 |
|
0 |
5 |
8 |
|
-5 |
5 |
23 |
|
-2 |
2 |
9 |
|
0 |
4 |
24 |
|
-2 |
3 |
10 |
|
-3 |
3 |
25 |
|
0 |
4 |
11 |
|
0 |
4 |
26 |
|
-3 |
3 |
12 |
|
0 |
8 |
27 |
|
-3 |
3 |
13 |
|
0 |
6 |
28 |
|
0 |
4 |
14 |
|
-3 |
2 |
29 |
|
-2 |
3 |
15 |
|
-4 |
-1 |
30 |
|
-2 |
2 |
Задание №6
Тема. Интерполяционный кубический сплайн.
Задание: Построить интерполяционный кубический сплайн для функции, заданной таблицей. На графике отобразить узлы интерполяции и сплайн.
Варианты индивидуальных заданий.
Номер варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
xk |
yk |
yk |
yk |
yk |
yk |
yk |
yk |
yk |
0.25 |
0.7788 |
1.284 |
0.2474 |
0.2526 |
1.031 |
0.2449 |
0.2553 |
2.034 |
0.31 |
0.7334 |
1.363 |
0.3051 |
0.3150 |
1.048 |
0.3004 |
0.3203 |
2.051 |
0.36 |
0.6977 |
1.433 |
0.3523 |
0.3678 |
1.066 |
0.3452 |
0.3764 |
2.066 |
0.39 |
0.6771 |
1.477 |
0.3802 |
0.4000 |
1.077 |
0.3714 |
0.4111 |
2.078 |
0.43 |
0.6505 |
1.537 |
0.4169 |
0.4434 |
1.094 |
0.4053 |
0.4586 |
2.093 |
0.47 |
0.6250 |
1.600 |
0.4529 |
0.4875 |
1.112 |
0.4382 |
0.5080 |
2.112 |
0.52 |
0.5945 |
1.682 |
0.4969 |
0.5438 |
1.138 |
0.4777 |
0.5726 |
2.137 |
0.56 |
0.5712 |
1.751 |
0.5312 |
0.5897 |
1.161 |
0.5080 |
0.6269 |
2.161 |
0.64 |
0.5273 |
1.896 |
0.5972 |
0.6846 |
1.212 |
0.5649 |
0.7445 |
2.197 |
0.66 |
0.5169 |
1.935 |
0.6131 |
0.7090 |
1.226 |
0.5784 |
0.7761 |
2.226 |
0.71 |
0.4916 |
2.034 |
0.6518 |
0.7712 |
1.263 |
0.6107 |
0.8595 |
2.263 |
Номер варианта |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
xk |
yk |
yk |
yk |
yk |
yk |
yk |
yk |
yk |
0.24 |
1.2711 |
0.2355 |
1.029 |
0.7866 |
0.2423 |
0.2447 |
0.2374 |
1.6866 |
0.26 |
1.297 |
0.2544 |
1.034 |
0.7711 |
0.2629 |
0.2660 |
0.2571 |
1.6711 |
0.27 |
1.310 |
0.2637 |
1.037 |
0.7634 |
0.2733 |
0.2768 |
0.2667 |
1.6634 |
0.29 |
1.336 |
0.2823 |
1.042 |
0.7483 |
0.2941 |
0.2984 |
0.2860 |
1.6483 |
0.30 |
1.350 |
0.2915 |
1.045 |
0.7408 |
0.3045 |
0.3093 |
0.2955 |
1.6408 |
0.32 |
1.377 |
0.3097 |
1.052 |
0.7261 |
0.3255 |
0.3314 |
0.3146 |
1.6261 |
0.37 |
1.448 |
0.3544 |
1.069 |
0.6907 |
0.3785 |
0.3879 |
0.3616 |
1.5907 |
0.38 |
1.462 |
0.3631 |
1.073 |
0.6839 |
0.3892 |
0.3994 |
0.3709 |
1.5839 |
0.42 |
1.522 |
0.3976 |
1.090 |
0.6570 |
0.4325 |
0.4466 |
0.4078 |
1.5570 |
0.49 |
1.632 |
0.4556 |
1.122 |
0.6126 |
0.5098 |
0.5334 |
0.4706 |
1.5126 |
0.59 |
1.804 |
0.5330 |
1.179 |
0.5543 |
0.6248 |
0.6696 |
0.5564 |
1.4543 |
Номер варианта |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
xk |
yk |
yk |
yk |
yk |
yk |
yk |
yk |
1.2 |
0.0792 |
0.1823 |
1.063 |
0.3012 |
1.492 |
0.6703 |
0.7293 |
1.3 |
0.1139 |
0.2624 |
1.091 |
0.2725 |
1.935 |
0.5169 |
1.0495 |
1.4 |
0.1461 |
0.3365 |
1.119 |
0.2466 |
2.293 |
0.4350 |
1.3459 |
1.6 |
0.2041 |
0.4700 |
1.170 |
0.2019 |
3.561 |
0.2800 |
1.8800 |
1.7 |
0.2304 |
0.5306 |
1.193 |
0.1827 |
3.935 |
0.2541 |
2.1225 |
1.9 |
0.2788 |
0.6419 |
1.239 |
0.1496 |
4.055 |
0.2466 |
2.5674 |
2.1 |
0.3222 |
0.7419 |
1.281 |
0.1225 |
4.665 |
0.2144 |
2.9677 |
2.2 |
0.3424 |
0.7885 |
1.301 |
0.1108 |
5.529 |
0.1809 |
3.1538 |
2.4 |
0.3802 |
0.8755 |
1.339 |
0.0907 |
7.538 |
0.1327 |
3.5019 |
2.6 |
0.4150 |
0.9555 |
1.375 |
0.0743 |
12.182 |
0.0821 |
3.8220 |
2.7 |
0.4314 |
0.9933 |
1.392 |
0.0672 |
16.281 |
0.0614 |
3.9730 |
Номер варианта |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
xk |
yk |
yk |
yk |
yk |
yk |
yk |
yk |
1.24 |
0.8604 |
1.2350 |
0.8539 |
1.1973 |
2.0127 |
0.6419 |
0.9929 |
1.27 |
0.9561 |
1.1980 |
0.6824 |
0.9863 |
1.7427 |
0.5993 |
0.8473 |
1.3 |
1.0495 |
1.1626 |
0.5727 |
0.8518 |
1.5792 |
0.5664 |
0.7512 |
1.32 |
1.1105 |
1.1398 |
0.5190 |
0.7863 |
1.5038 |
0.5477 |
0.7029 |
1.34 |
1.1707 |
1.1177 |
0.4756 |
0.7336 |
1.4462 |
0.5310 |
0.6629 |
1.37 |
1.2592 |
1.0855 |
0.4241 |
0.6712 |
1.3834 |
0.5085 |
0.6139 |
1.4 |
1.3459 |
1.0547 |
0.3840 |
0.6229 |
1.3403 |
0.4884 |
0.5742 |
1.42 |
1.4026 |
1.0347 |
0.3617 |
0.5962 |
1.3195 |
0.4760 |
0.5515 |
1.45 |
1.4863 |
1.0058 |
0.3335 |
0.5626 |
1.2973 |
0.4589 |
0.5217 |
1.47 |
1.5410 |
0.9871 |
0.3174 |
0.5434 |
1.2872 |
0.4482 |
0.5042 |
1.49 |
1.5951 |
0.9689 |
0.3029 |
0.5264 |
1.2803 |
0.4380 |
0.4881 |