Контрольная работа №5 Приложения производной
201–210. Вычислить пределы, используя правило Лопиталя.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
211–220. Составить уравнение касательной и нормали к графику функции в точке с абсциссой .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
221–230. Найти наибольшее и наименьшее значения функции f(x) на отрезке [a;b].
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
231–240. Провести полное исследование функции и построить график.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
241–250.
Даны
три населённых пункта
,
и
,
причём
и
S км.
Из пункта
в пункт
выезжает автомобиль, движущийся со
скоростью
км/ч;
одновременно с ним из пункта
в пункт
выезжает поезд со скоростью
км/ч.
В какой момент времени (от начала
движения) расстояние между поездом и
автомобилем будет наименьшим? Сделать
чертёж.
|
S |
|
|
|
S |
|
|
|
|
200 |
80 |
50 |
|
220 |
88 |
55 |
|
|
260 |
104 |
65 |
|
160 |
64 |
40 |
|
|
320 |
128 |
80 |
|
300 |
120 |
75 |
|
|
140 |
56 |
35 |
|
240 |
96 |
60 |
|
|
280 |
112 |
70 |
|
180 |
72 |
45 |
Контрольная работа №6 Интегральное исчисление
251–260. Найти неопределенные интегралы. В а), б), в) результат проверить дифференцированием.
в)
г)
|
в)
г)
|
в)
г)
|
в)
г)
|
в)
г)
|
в)
г)
|
в)
г)
|
в)
г)
|
в)
г)
|
в)
г)
|
б)
б)
б)
б)
б)
б)
б)
б)
б)
б)
261–270. Вычислить определенные интегралы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
271–280. Вычислить: а) площадь фигуры, ограниченной заданными кривыми; б) объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями. Выполнить чертежи.
|
б)
|
|
б)
|
|
б)
|
|
б)
|
|
б) |
|
б)
|
|
б)
|
|
б)
|
|
б)
|
|
б)
|
,
,
,
,
,
,
,
,
,
,
281–290. Решить задачи с применением определённого интеграла.
1) Скорость движения точки изменяется по закону v=v(t). Найти путь, пройденный точкой от начала движения до её остановки.
2) В спокойном состоянии пружина имеет длину 20 см. Сила в 50 Н растягивает пружину на 1 см. Найти работу, которую нужно произвести, чтобы растянуть пружину от a до b см.
3) Треугольна пластинка с основанием a см и высотой b см погружена вертикально в воду так, что её вершина лежит на поверхности воды, а основание параллельно ей. Найти силу давления воды на пластинку.
|
v(t) |
a |
b |
|
v(t) |
a |
b |
|
|
|
21 |
42 |
|
|
22 |
44 |
|
|
|
23 |
46 |
|
|
24 |
48 |
|
|
|
25 |
50 |
|
|
26 |
52 |
|
|
|
27 |
54 |
|
|
28 |
56 |
|
|
|
29 |
58 |
|
|
30 |
60 |
291–300. Вычислить несобственные интегралы или установить их расходимость.
|
|
|
|
|
|
|
|
|
|
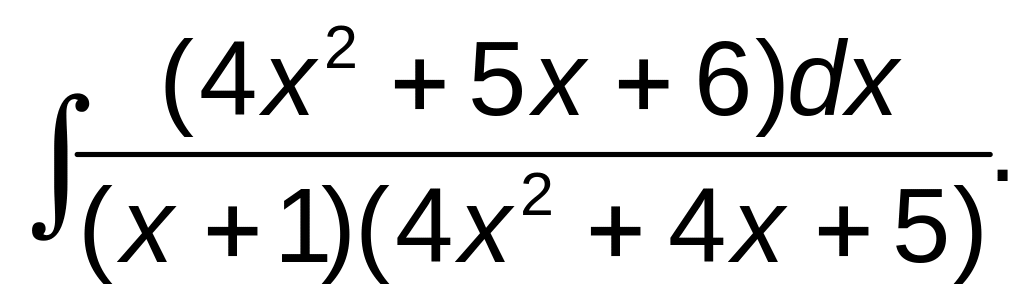
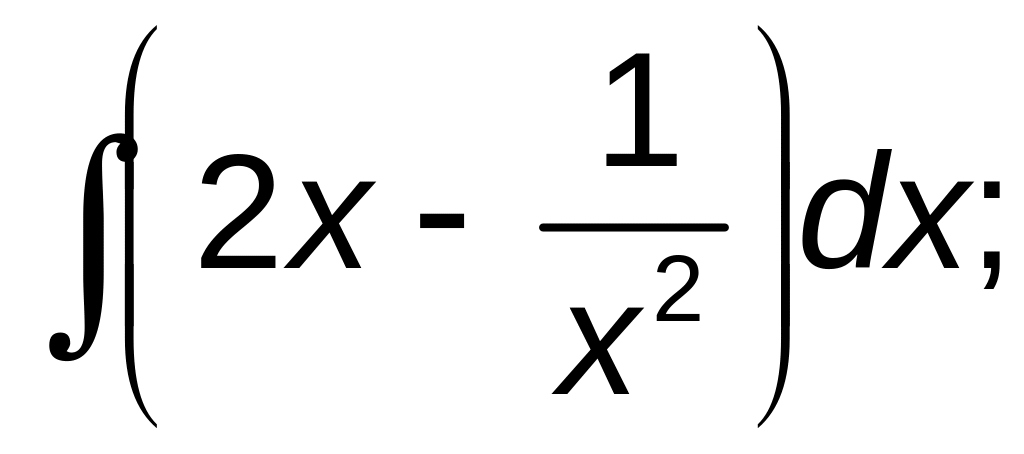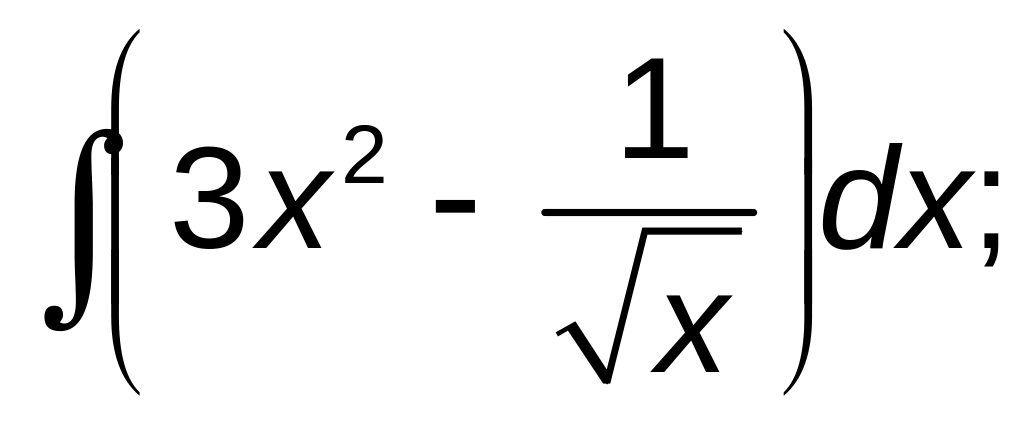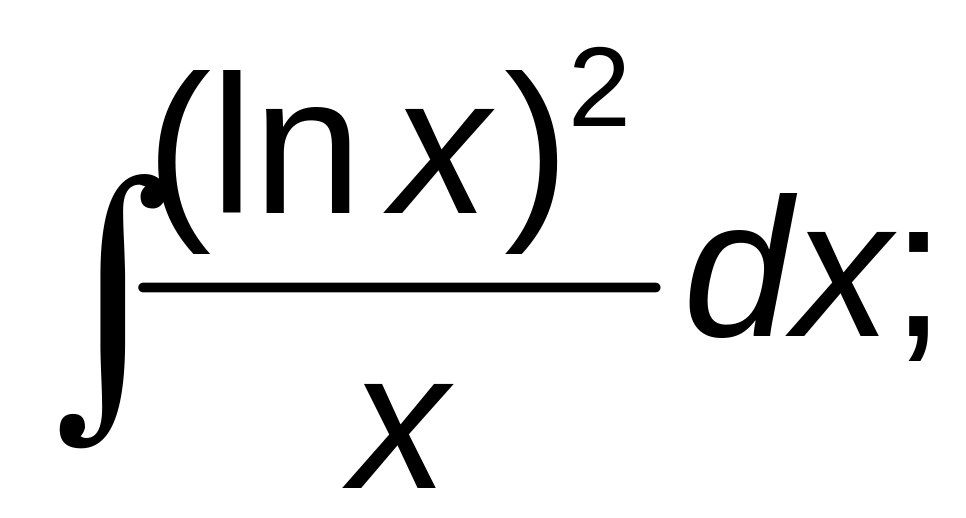
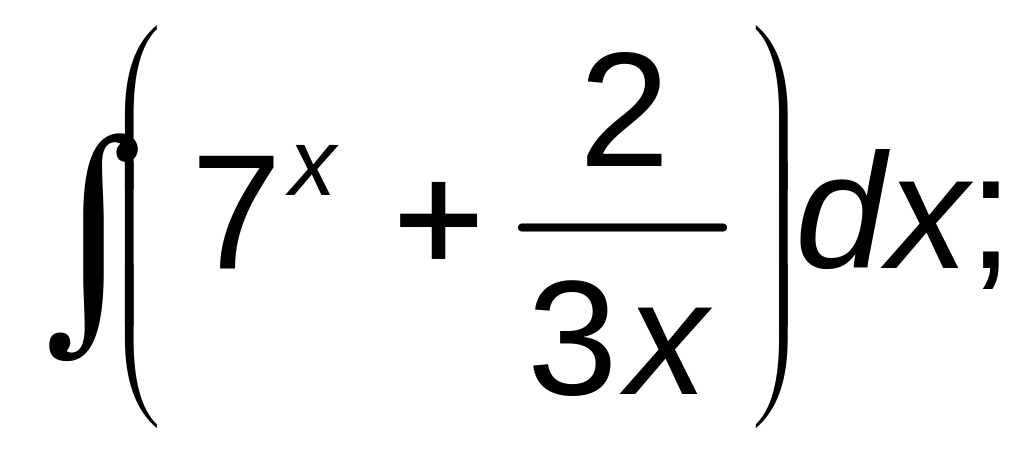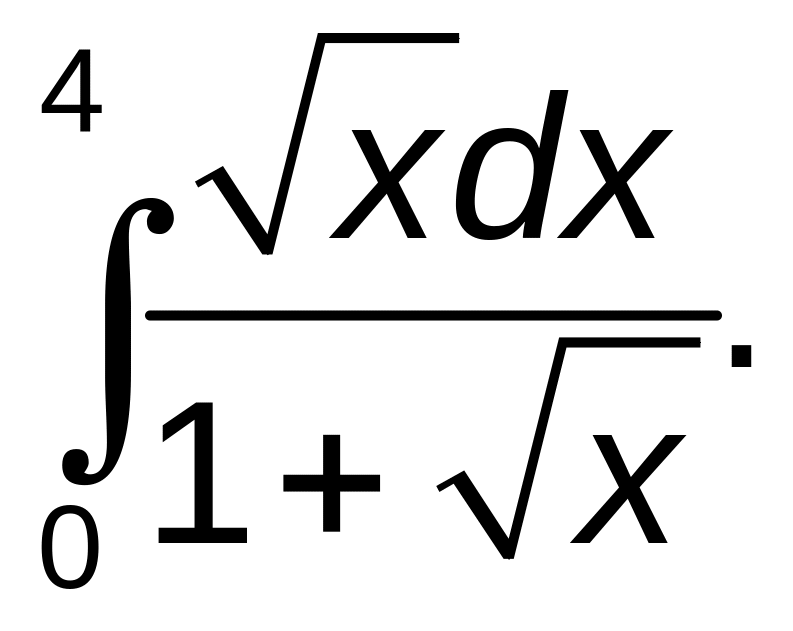
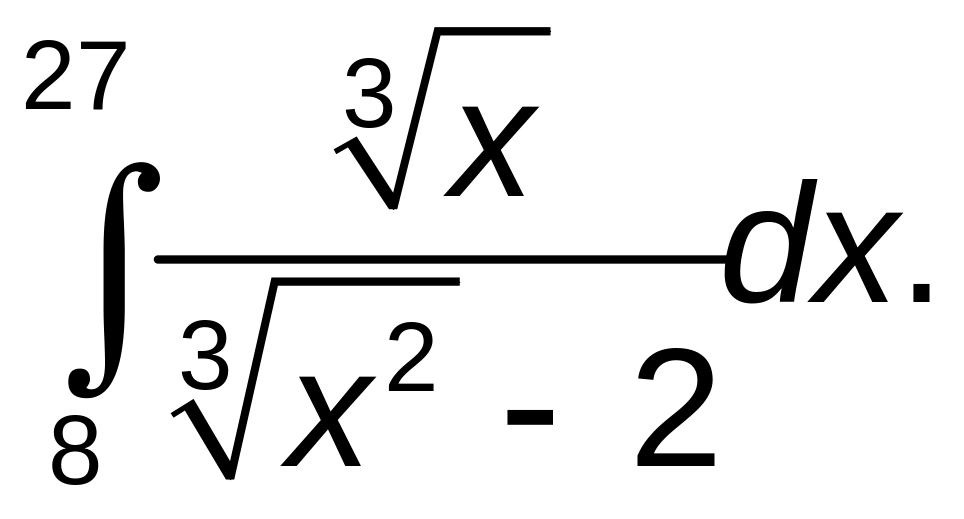
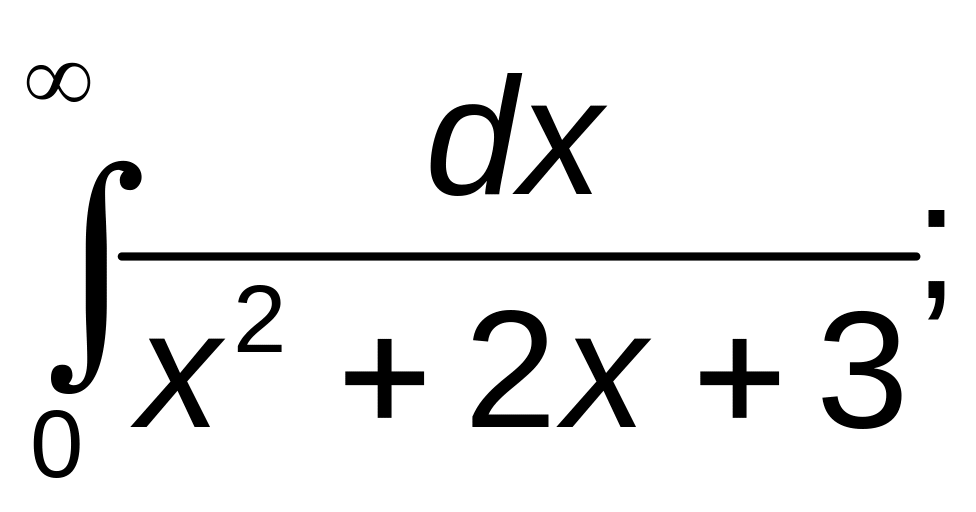б)
б)
б)
б)
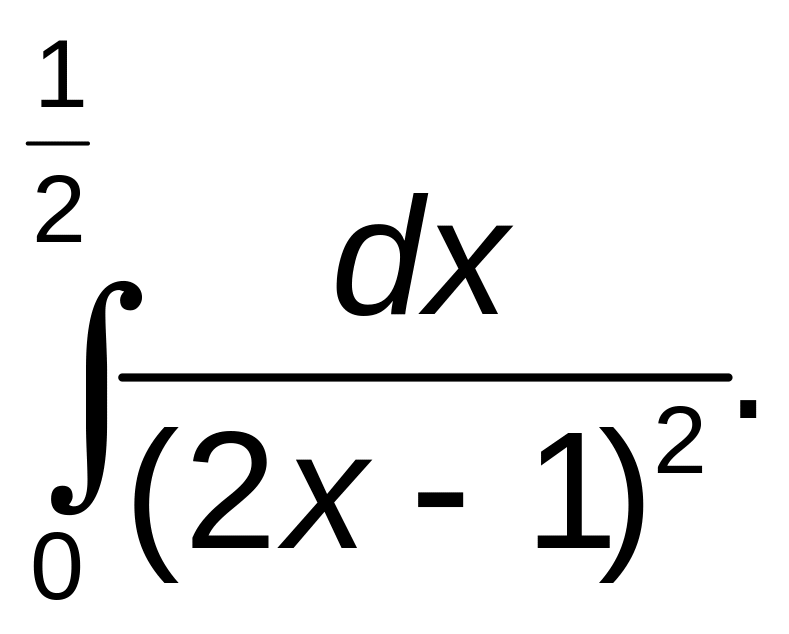
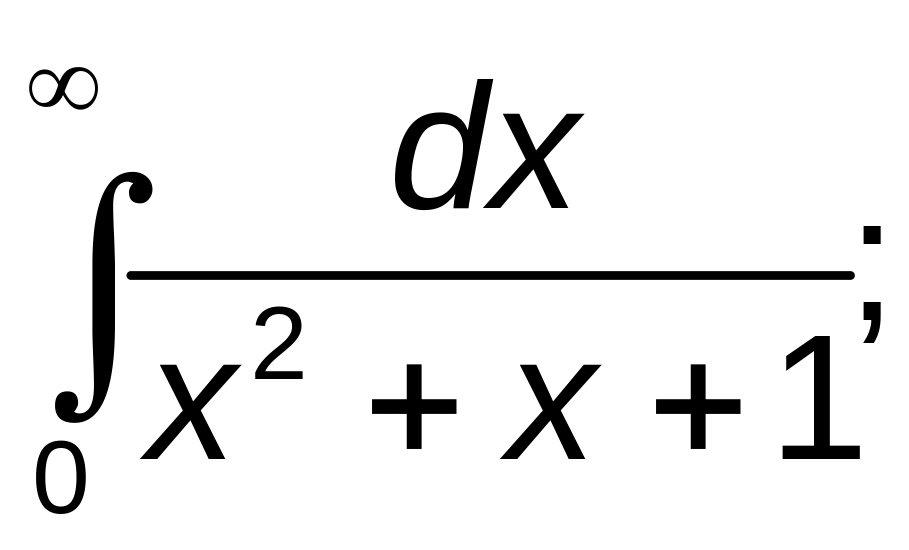б)
б)
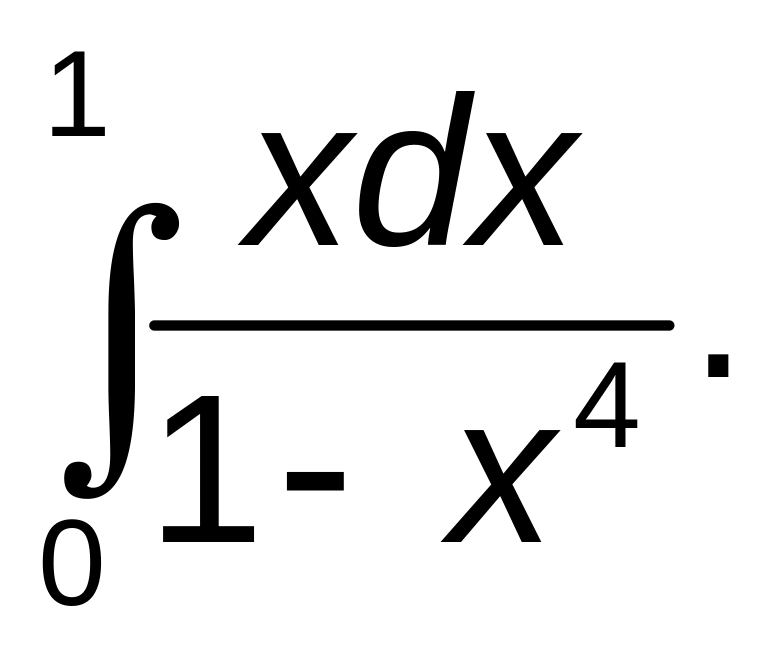
б)
б)
б)
б)
