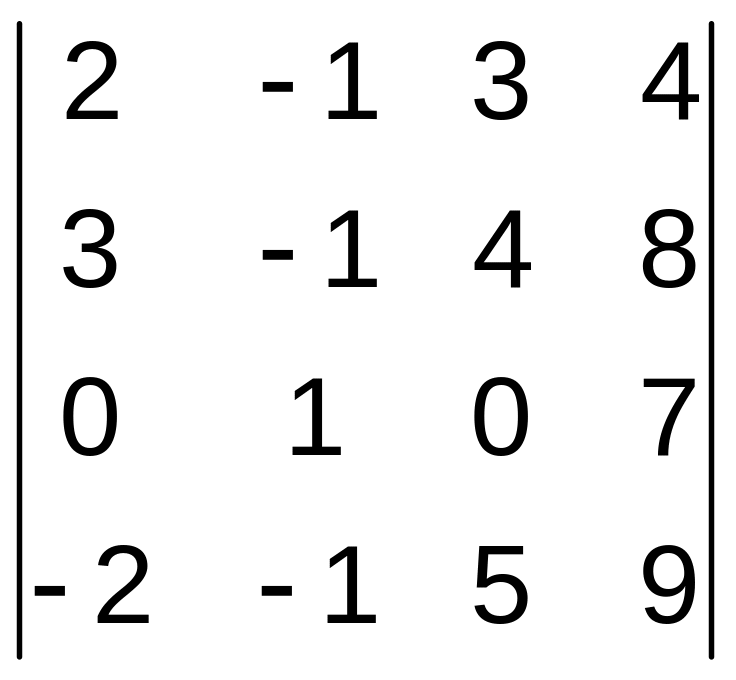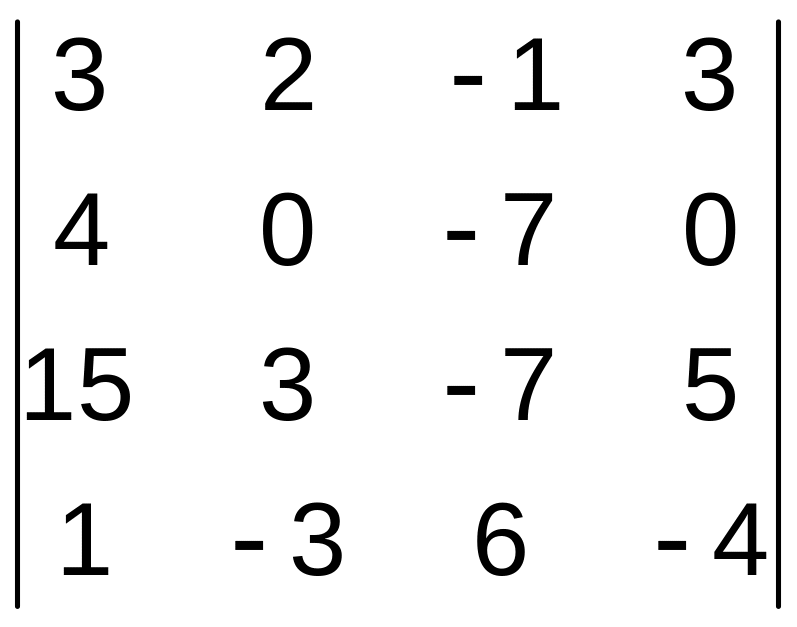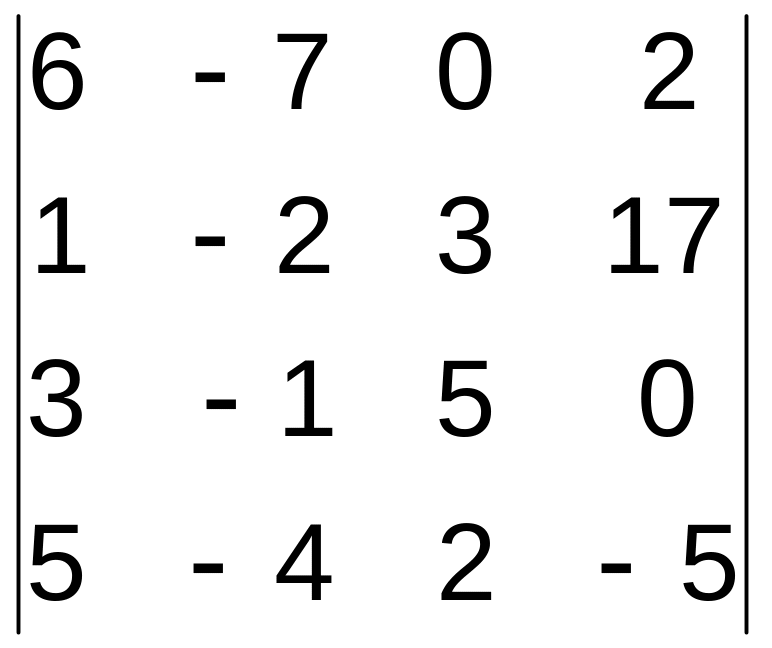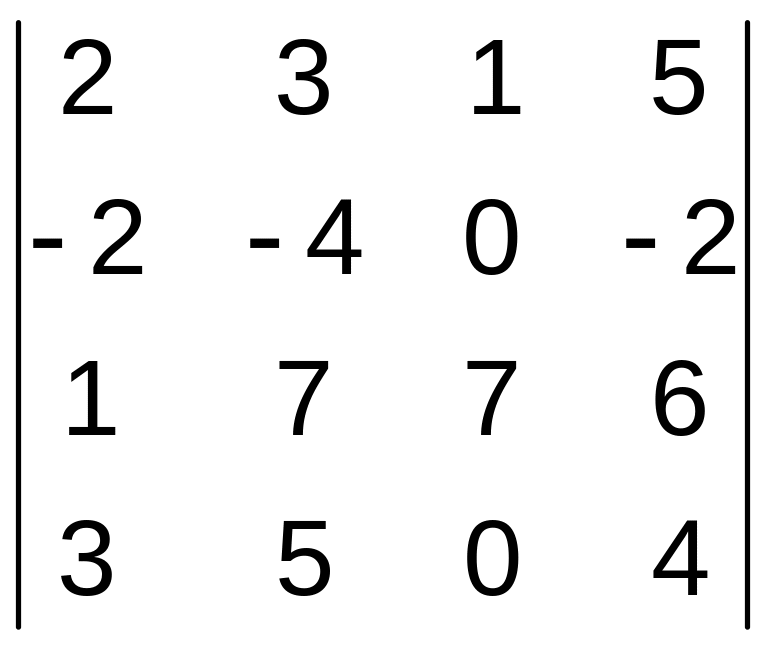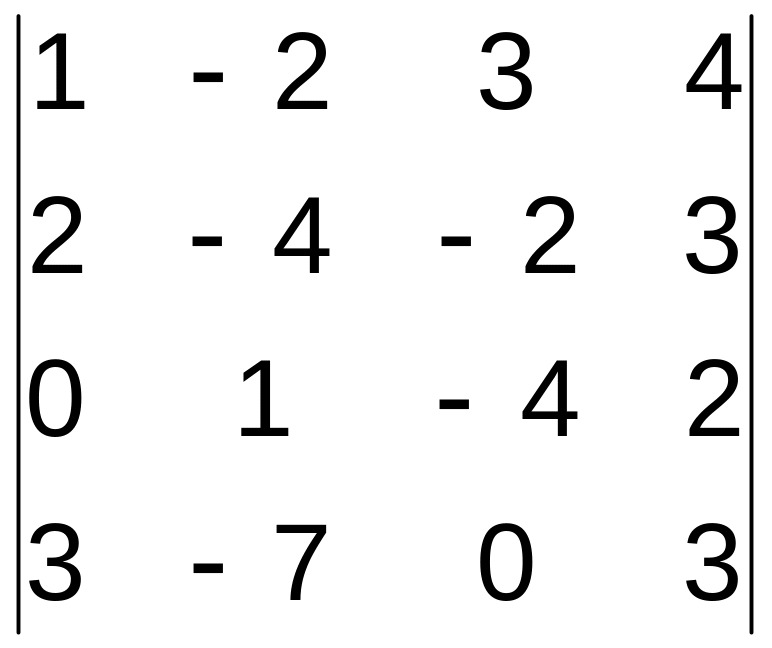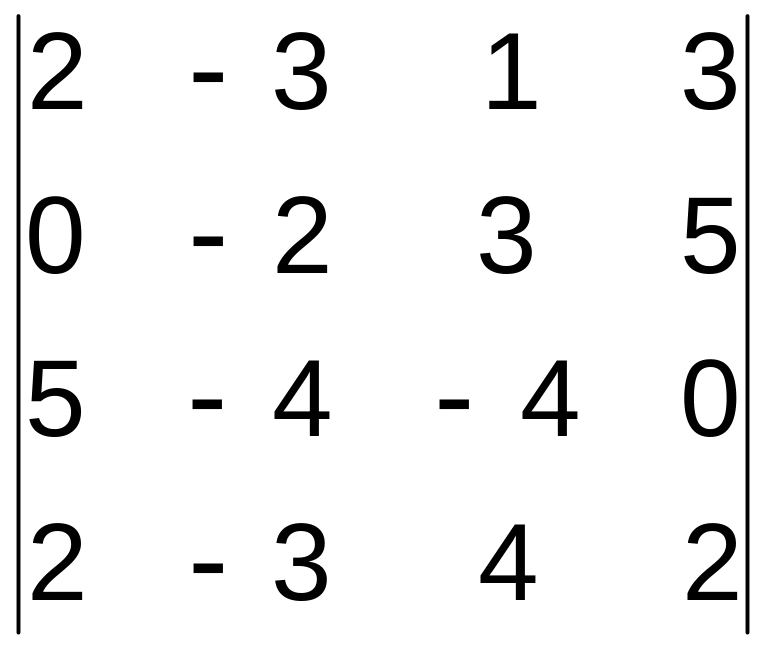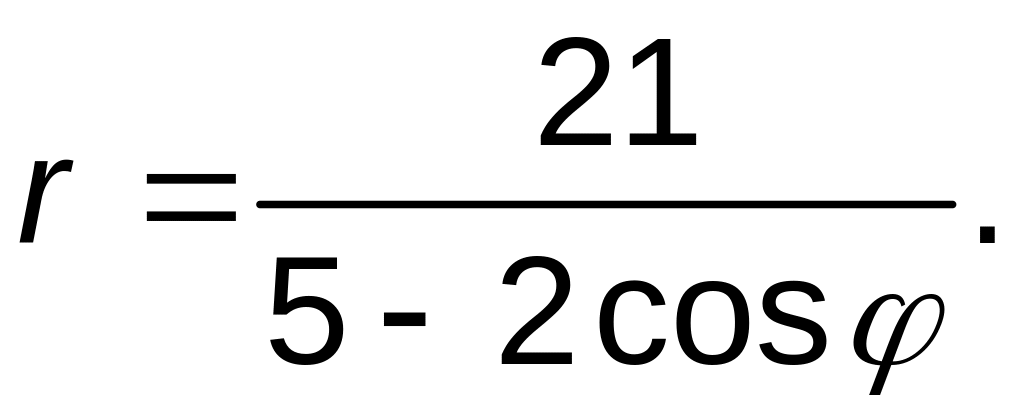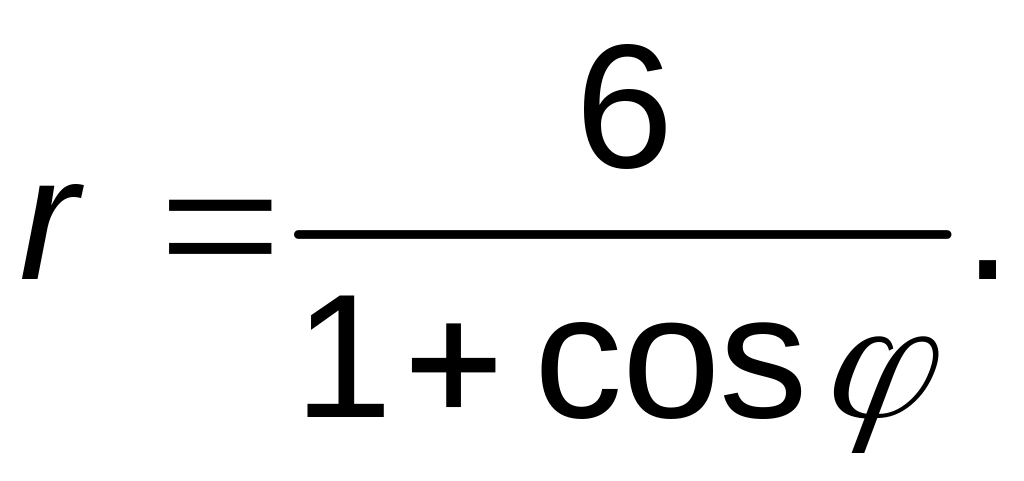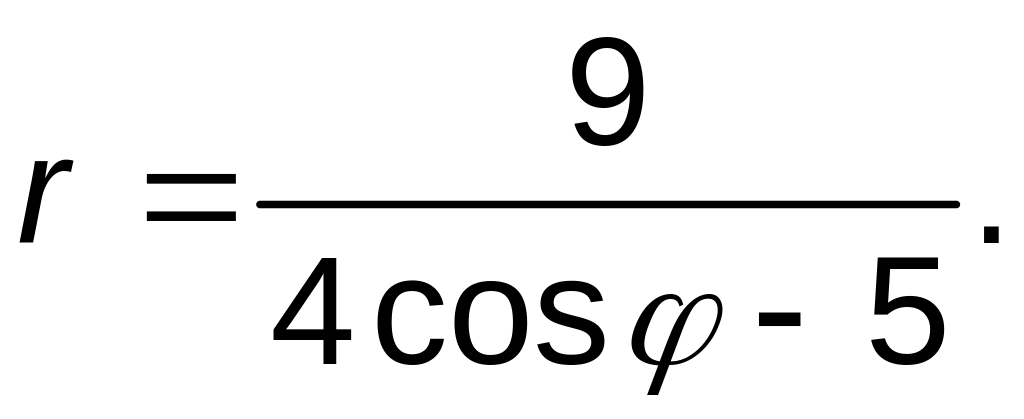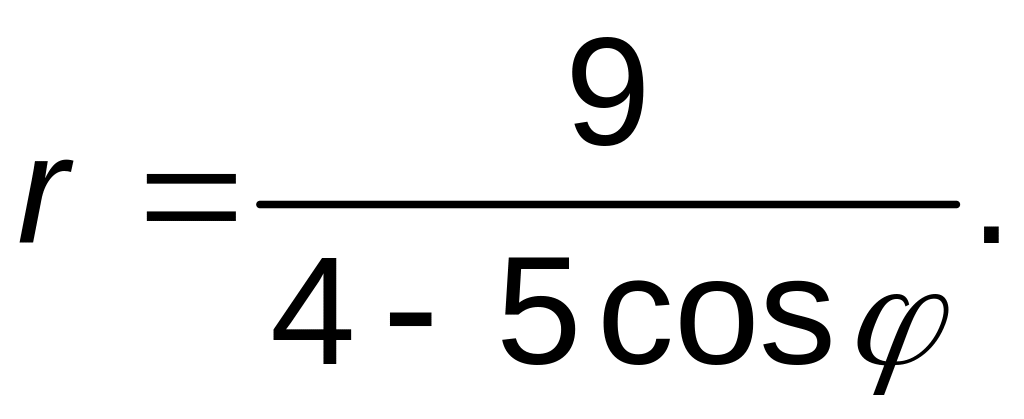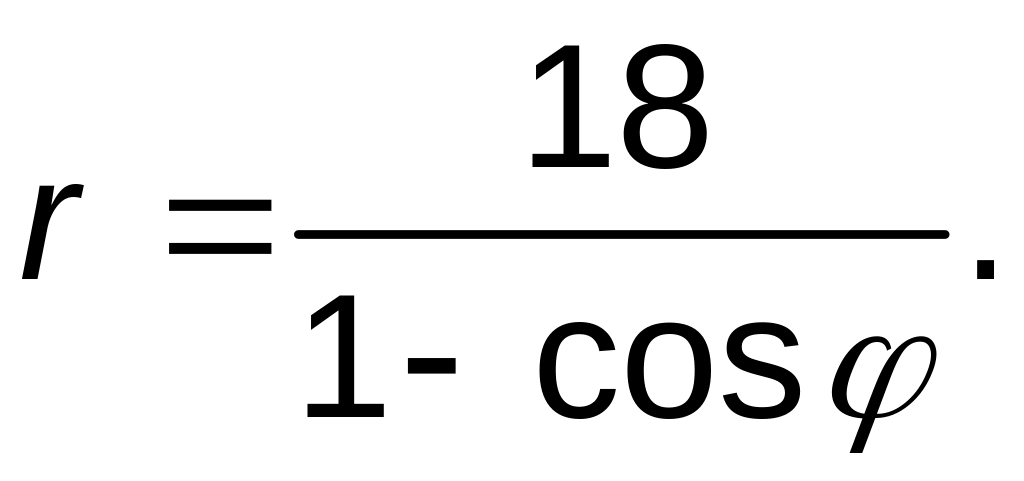3. Задания к контрольным работам Контрольная работа №1 Линейная алгебра
1–10.
Дано комплексное число
.
Требуется: 1) записать число
в алгебраической, тригонометрической
и показательной формах; 2) найти все
корни уравнения
и изобразить их на комплексной плоскости.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11–20.
Найти неизвестную матрицу
из заданного уравнения.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21–30. Вычислить определитель четвертого порядка.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31–40. Проверить совместность системы уравнений и в случае совместности решить её: а) по формулам Крамера; б) методом обратной матрицы; в) методом Гаусса.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41–50.
Даны векторы
в декартовой системе координат. Показать,
что векторы
образуют базис. Найти координаты вектора
в этом базисе (написать разложение
вектора
в базисе
).
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
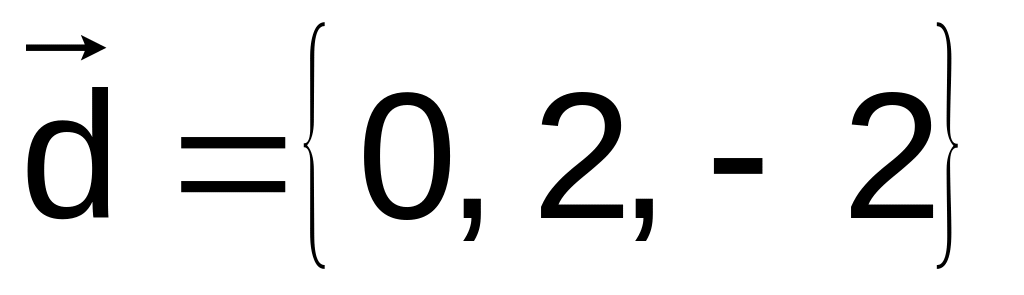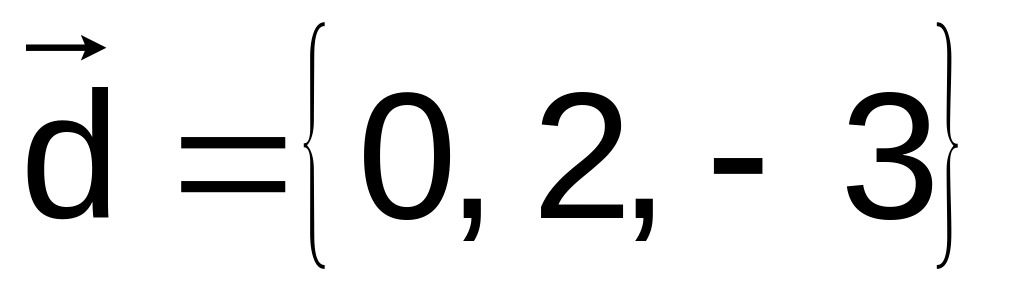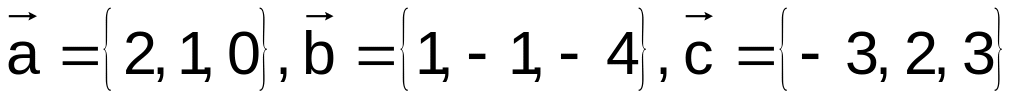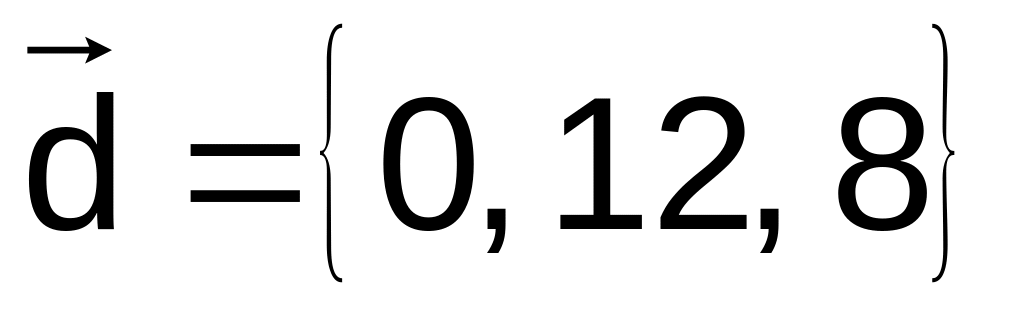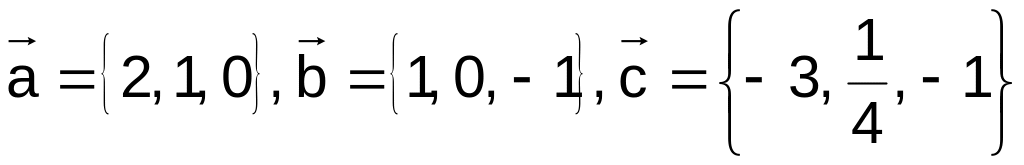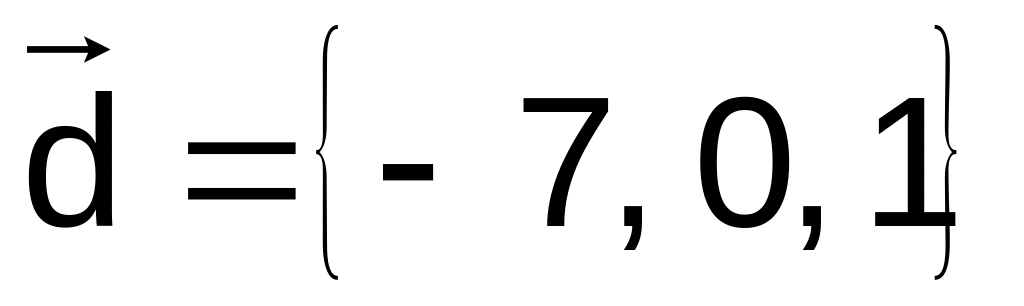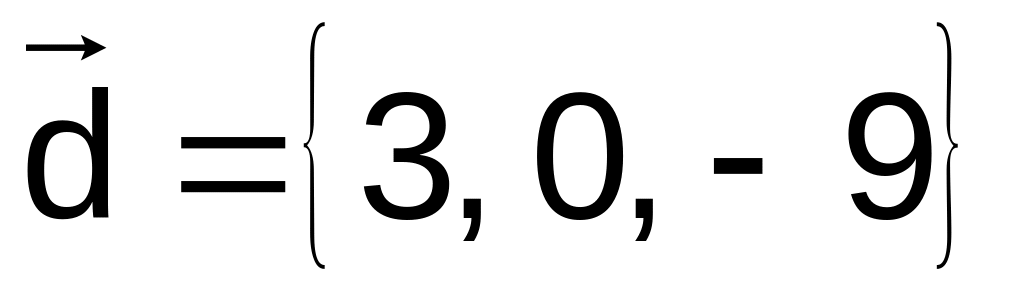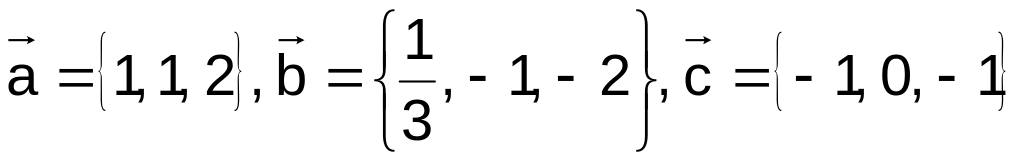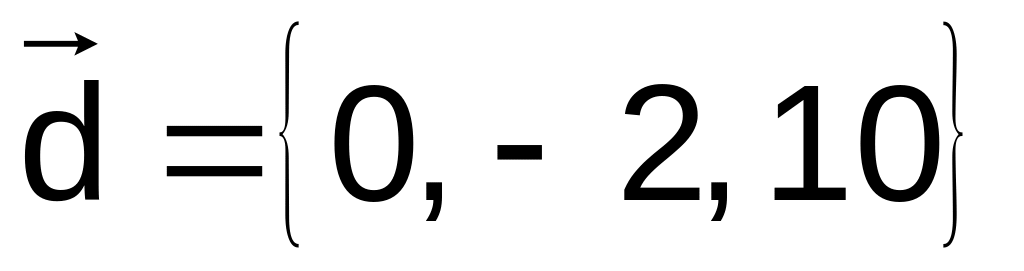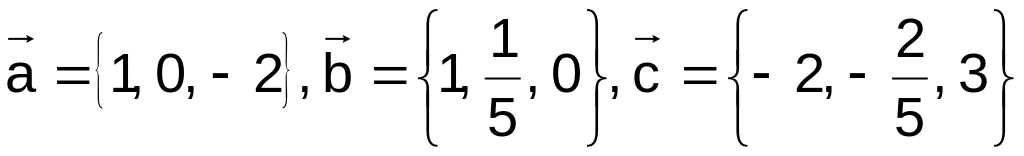Контрольная работа №2 Аналитическая геометрия
51–60. Даны вершины треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах; 4) уравнение медианы, проведенной из вершины В; 5) уравнение высоты СD и ее длину; 6) уравнение окружности, для которой высота СD есть диаметр, и точки пересечения этой окружности со стороной АС; 7) уравнение биссектрисы внутреннего угла А; 8) площадь треугольника АВС; 9) систему линейных неравенств, определяющих треугольник АВС. Сделать чертеж.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
61–70.
Даны силы
,
и координаты точки М. Найти:
1) равнодействующую силу
сил
и
,
ее величину и направляющие косинусы;
2) работу силы
при перемещении ее точки приложения из
начала координат в точку М; 3) момент
силы
,
приложенной к началу координат,
относительно точки М. Сделать чертеж.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
. |
|
|
|
,
,
.
,
,
.
,
,
.
,
,
.
,
,
.
,
,
.
,
,
.
,
,
.
,
,
,
.
71–80.
Даны координаты вершин пирамиды
,
,
,
.
Найти: 1) длину ребра
;
2) угол между ребрами
и
;
3) угол между ребром
и гранью
;
4) площадь грани
;
5) объем пирамиды;
6) уравнение прямой
;
7) уравнение плоскости
;
8) уравнение высоты,
опущенной из вершины
на грань
и ее длину; 9) координаты
центра тяжести пирамиды, считая плотность
постоянной. Сделать чертеж.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
81–90.
Составить уравнение геометрического
места точек, для каждой из которых
отношение расстояния до данной точки
к расстоянию до данной прямой
(или
)
равно числу k.
Полученное уравнение привести к
каноническому виду и построить кривую.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
91–100.
Линия задана уравнением
в полярной системе координат. Требуется:
1) построить линию по точкам, от
до
;
2) найти
уравнение данной линии в прямоугольной
декартовой системе координат, у которой
начало совпадает с полюсом, а положительная
полуось абсцисс – с полярной осью; 3) по
полученному уравнению определить, какая
это линия.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
