2. Методические указания

К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

Рассмотрим примеры решения некоторых задач.

Пример 1. Дано комплексное число . Требуется: 1) записать число в алгебраической, тригонометрической и показательной формах; 2) найти все корни уравнения и изобразить их на комплексной плоскости.

Решение. Алгебраическая форма комплексного числа: , где – действительная, – мнимая части комплексного числа; тригонометрическая форма: ; показательная форма: , где - модуль,  - аргумент комплексного числа.

Справедливы следующие формулы: ,

Все значения корня -й степени из комплексного числа находятся по формуле Муавра:

, где .1)

Для того, чтобы представить число в алгебраической форме, умножаем числитель и знаменатель на выражение, сопряжённое знаменателю:

.

Найдём модуль и аргумент числа :

- модуль.

- аргумент.

Тогда – тригонометрическая форма;

– показательная форма комплексного числа .

2) Найдём корни уравнения , т.е. все значения .

,

,

,

,

.

Изобразим корни уравнения точками на комплексной плоскости (рис. 2.1).

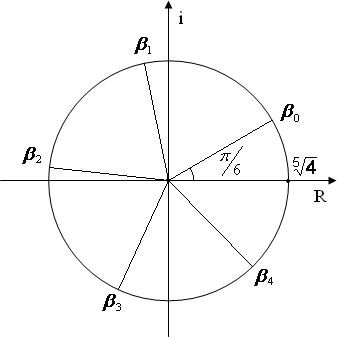
Рис. 2.1. Корни уравнения z⁵ - a=0

Пример 2. Даны векторы , , , и . Показать, что векторы образуют базис и найти координаты вектора в этом базисе.

Решение. Система векторов называется линейно независимой, если равенство

имеет место только при нулевых значениях коэффициентов. Система n линейно независимых векторов в n-мерном пространстве называется базисом этого пространства. По векторам базиса можно разложить любой вектор пространства, причём единственным образом. Коэффициенты такого разложения называются координатами вектора в данном базисе.

Составим определитель из координат векторов и вычислим его

Так как , то векторы образуют базис. Для вычисления координат вектора в этом базисе составим систему линейных уравнений

Решая эту систему, получаем , , , . Следовательно в рассматриваемом базисе, или

.

Пример 3. Линия задана уравнением в полярной системе координат. Требуется 1) построить линию по точкам; 2) найти уравнение данной линии в декартовой системе координат.

Решение. Составим таблицу значений и построим линию в полярной системе координат (рис. 2.2).

	0,
r	1,5	1,27	1,1	1,03	1	1,03	1,1	1,27
r	1,5	1,85	2,33	2,7	3	2,7	2,33	1,85

Для получения уравнений в декартовой системе координат используем формулы перехода от полярной системы координат к декартовой, приведённые в пункте «Комплексные числа». Получим

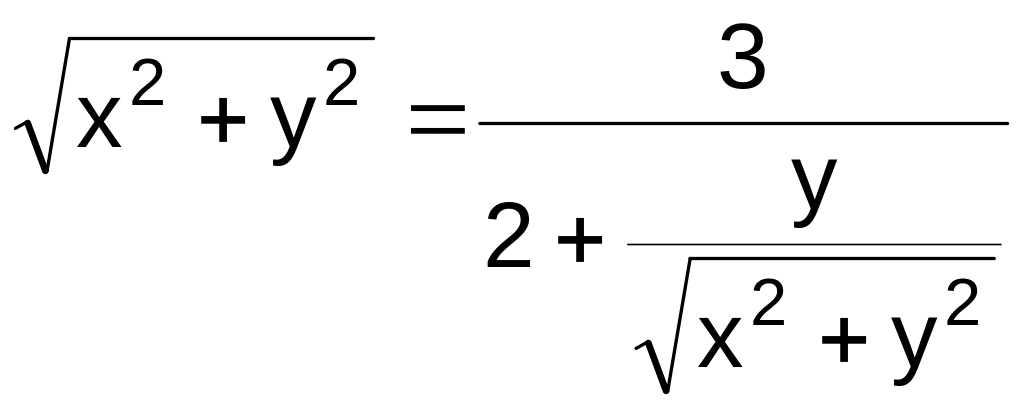, отсюда .

Рис. 2.2. Эллипс

Возводя обе части равенства в квадрат, выделив полный квадрат и произведя алгебраические преобразования, получим

– каноническое уравнение эллипса с центром в точке (0, -1), большой полуосью и малой полуосью

Пример 4. Вычислить пределы

1) ; 2) .

Решение. 1) Умножим числитель и знаменатель на выражение, сопряжённое знаменателю

2) Второй замечательный предел: , или .

Пример 5. Исследовать функцию на непрерывность; если имеются точки разрыва – определить их тип. Сделать чертёж.

Решение. Функция определена на всей числовой оси, кроме точки . Исследуем поведение функции в этой точке

Следовательно, в точке функция имеет бесконечный разрыв. Исследуем далее поведение функции в точке

Найденные односторонние пределы функции конечны, но различны. Поэтому в точке функция имеет конечный разрыв, величина скачка равна

Во всех остальных точках функция непрерывна. График представлен на рис. 2.3.

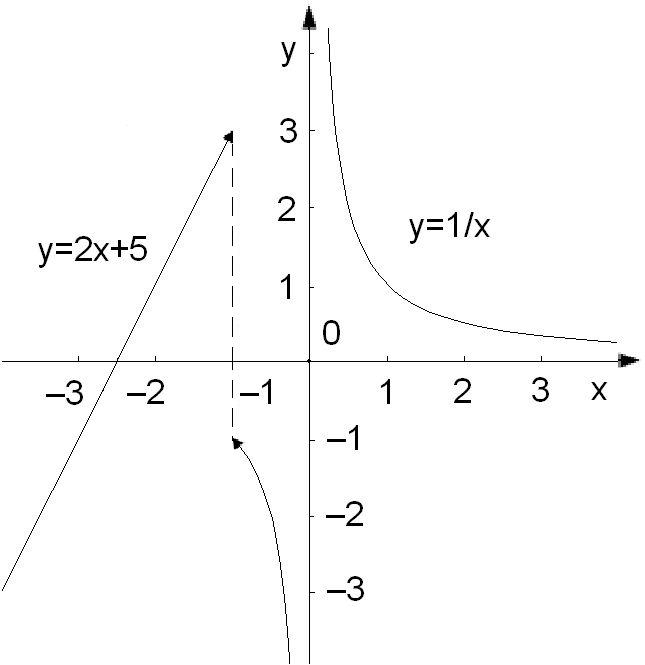
Рис. 2.3. График функции g(x)

Пример 6. Провести полное исследование и построить график функции

.

Решение. 1) Область определения .

2. Найдём асимптоты и точки разрыва функции. Прямые 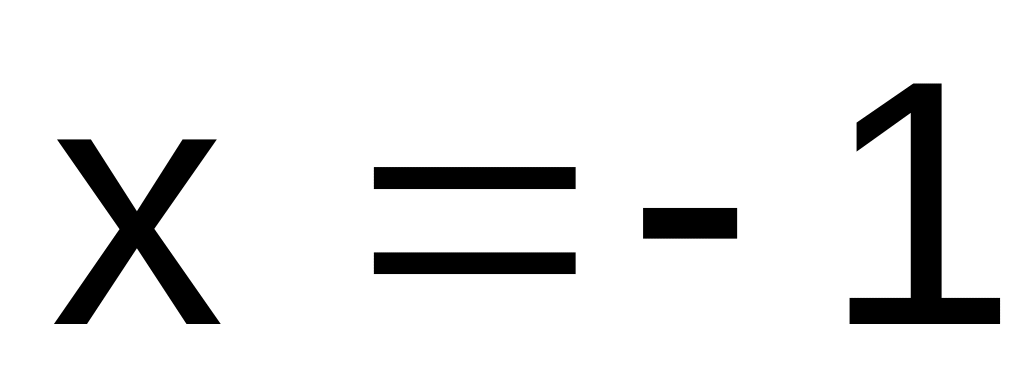и – вертикальные асимптоты.

Значит, и - точки разрыва второго рода.

. Наклонных асимптот нет.

, значит – горизонтальная асимптота.

2. , область определения симметрична относительно 0, следовательно функция является чётной.

3. Функция не является периодической.

4. Функция не является ограниченной.

5. Найдём нули функции

при , откуда или .

2. Определим промежутки знакопостоянства: при ;

Рис. 2.4. Промежутки знакопостоянств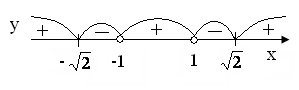а

, откуда . Тогда при .

2. С помощью производной первого порядка найдём промежутки возрастания и убывания функции

.

Рис. 2.5. Промежутки возрастания и убывания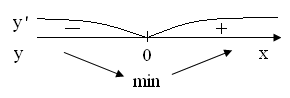

при . – точка локального минимума.

.

2. С помощью производной второго порядка найдём промежутки выпуклости и вогнутости функции

.

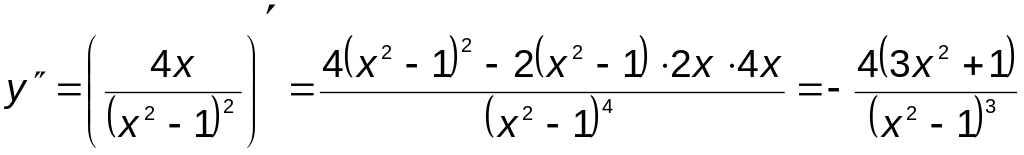Рис. 2.6. Промежутки выпуклости и вогнутости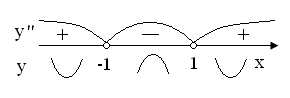

Таким образом, при всех . В точках , вторая производная не существует.

2. Построим график (рис. 2.7).

Рис. 2.7. График функции y=f(x)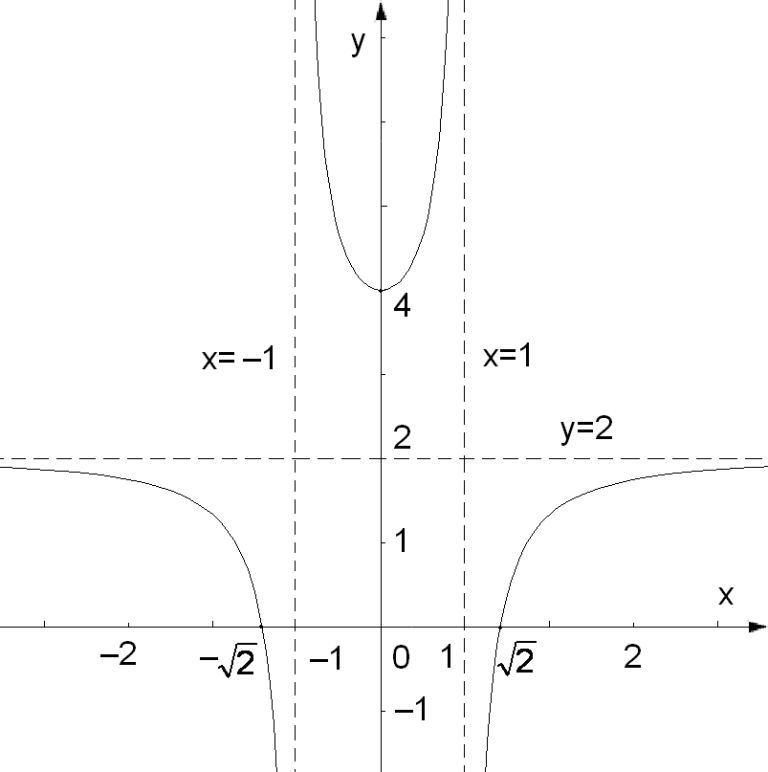

Пример 7. Найти неопределенные интегралы

1) ; 2)

Решение. 1)

2) Разложим дробь на простейшие

Решая систему уравнений

получим , , .

Отсюда

Пример 8. Скорость движения точки изменяется по закону м/с. Найти путь, пройденный точкой за четвёртую секунду.

Решение. Согласно условию, Отсюда

(м).

Пример 9. Сжатие x винтовой пружины пропорционально приложенной силе F. Вычислить работу силы F при сжатии пружины на 0,04 м, если для сжатия её на 0,01 м нужна сила 10 Н.

Решение. Так как x=0,01 м при F=10 Н, то, подставляя эти значения в равенство F=kx, получим 10=k·0,01, откуда k=1000 Н/м. Искомую работу найдём с помощью определённого интеграла

(Дж).

Пример 10. Треугольная пластинка с основанием 0,2 м и высотой 0,4 м погружена вертикально в воду так, что вершина лежит на поверхности воды, а основание параллельно ей. Плотность воды кг/м³. Вычислить силу давления воды на пластинку.

Решение. Выделим на глубине горизонтальную полоску шириной (рис. 2.8). Изменение глубины на малую величину вызовет изменение силы давления Р на малую величину . Площадь полоски

Из подобия треугольников АВС и DЕС имеем , откуда Следовательно,

Элементарная сила давления (Н) составляет

Интегрируя при изменении от 0 до 0,4, получим

 (Н).

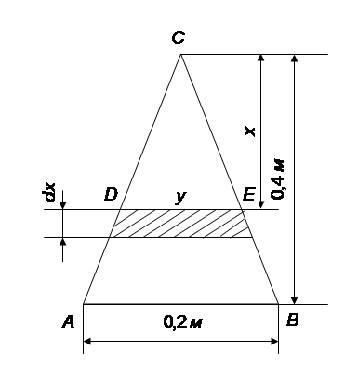
Рис 2.8. Треугольная пластинка