13.3. Метод трапеций

Этот метод основан на свойствах ВЧХ, следующих из полученной ранее формулы, которые мы рассмотрим без доказательств.

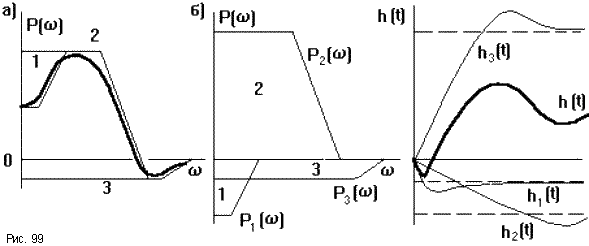
1. Свойство линейности: если ВЧХ можно представить суммой  P( ) = SPi( ), то каждой составляющей Pi( ) будет соответствовать составляющая переходной характеристики

 

,

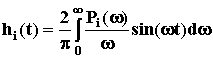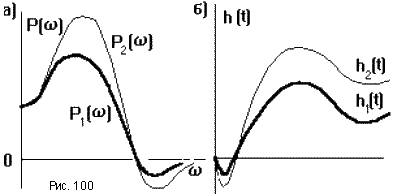при этом h(t) = (рис.99а). Поэтому, если ВЧХ имеет сложную форму, ее можно представить суммой трапециидальных ВЧХ, примыкающих к вертикальной оси. Затем все трапеции перерисовывают, перенося их основания на горизонтальную ось (рис.99б). Каждой такой трапеции соответствует своя составляющая переходной характеристики h_i(t), имеющая апериодический характ ер (рис.99в). Результирующая кривая строится суммированием данных составляющих.

2. Если умножить P( ) на постоянный множитель а, то соответствующая ей h(t) также умножается на а. То есть, чем выше ВЧХ, тем выше и переходная характеристика (рис.100).

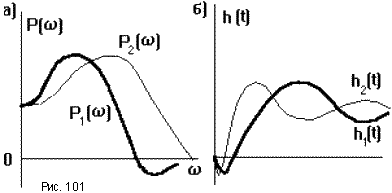
3. Если аргумент w в выражении ВЧХ P( ) умножить на постоянный множитель а, то аргумент в h(t) будет делиться на это число, то есть

 

.

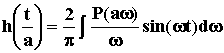То есть переходный процесс в случае P(a ) будет протекать в а раз быстрее, чем в случае P( ) (рис.101).

Рассмотрим трапециидальную ВЧХ (рис.102а). Она характеризуется коэффициентом наклона k = _{1 2}. Под единичной трапецией (рис.102б) понимают трапецию, две стороны которой совпадают с осями координат и равны по 1 в соответствующих масштабах; наклон k может быть различным: P₁( ) = .

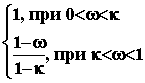Подставляя это определение в выражение для определения h(t) можно вычислить кривую переходного процесса, соответствующую единичной трапециидальной ВЧХ. Эти расчеты были проделаны и составлены таблицы h_k -функций.

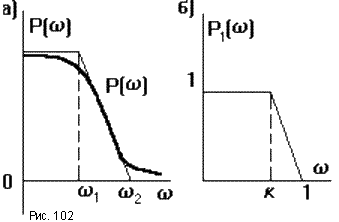
Для любой трапециидальной ВЧХ, на которые разбита реальная ВЧХ (рис.99б), можно построить подобную ей единичную трапецию со значением k = _{1 2}, где ₁ - частота, соответствующая перелому реальной трапеции, ₂ - основание трапеции реальной ВЧХ. Для данной единичной трапеции по таблице h_k-функций строят кривую h_k(k,t), где t - время. Затем, используя свойства 2 и 3 масштабирования ВЧХ и переходной характеристики строят кривую переходного процесса, соответствующего данной трапециидальной ВЧХ. Причем оба описанных процесса можно совместить: сначала задаются моментом времени t, для него по таблице находят значение h_k(k,t), потом умножают это значение на P(0) (масштабирование по вертикальной оси) и откладывают полученное значение на графике h(t) для времени t = t/ ₂ (масштабирование по горизонтальной оси). Строя таким образом точки для различных моментов времени получают кривую

h_i(t/ ₂) = P(0) h_k(k,t).

Данный алгоритм удобно оформить в таблицу:

t	hk(k,t)	t = t/ 2	hi(t) = P(0) hk(k,t)
.....	.....	.....	.....

После суммирования составляющих переходного процесса, соответствующих каждой трапеции, получают реальную характеристику h(t).

Описанный метод построения переходной характеристики называется методом трапеций.