1) Безынерционное звено:

  W₁ = K₁ = 100 => L(w) = 20lg100 = 40;

2) форсирующее звено:

  W₂ = p + 1;

его параметры:

  K₂ = 1, T₂ = 1, ₂ = 1/T₂ = 1;

3) Интегрирующее звено:

  W₃ = 1/p;

его ЛАЧХ проходит через точку L = 0 при частоте = 1;

4) Апериодическое звено:

  W₄ = 1/(0.1p + 1);

его параметры: K₄ = 1, T₄ = 0.1, ₄ = 1/T4 = 10.

Порядок построения ЛАЧХ и ЛФЧХ показан на рис.57.

Иногда требуется решить обратную задачу, то есть определить передаточную функцию по известной ЛАЧХ. Процедура определения передаточной функции состоит из следующих этапов:

1) известная ЛАЧХ представляется в асимптотическом виде, для этого непрерывная кривая заменяется отрезками прямых либо горизонтальных, либо с наклоном, кратным ±20 дб/дек;

2) асимптотическая ЛАЧХ раскладывается на ЛАЧХ элементарных звеньев;

3) для каждой из полученных ЛАЧХ определяются k и ₁ = 1/T и записывается передаточная функция типового звена;

4) передаточная функция САУ определяем путем перемножения передаточных функций типовых звеньев.

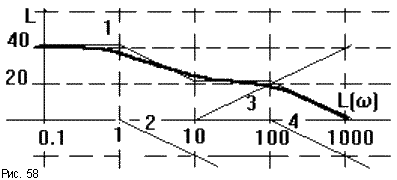
Описанный порядок иллюстрируется на рис.58.

Здесь ЛАЧХ может быть представлена суммой ЛАЧХ четырех типовых звеньев: пропорционального W₁ = 100, апериодического W₂ = 1/(p + 1), форсирующего W₃ = 0.1p + 1 и апериодического W₄ = 1/(0.01p + 1).

Таким образом, передаточная функция разомкнутой САУ имеет вид

  .

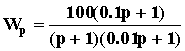В более сложных случаях наклоны ЛАЧХ на некоторых участках превышают ± 20дб/дек. Тогда помимо параметров K и T приходится определять еще и коэффициенты демпфирования r.

Зная передаточную функцию разомкнутой САУ можно построить ее уравнение динамики

 

 =>     =>

  => .

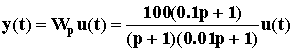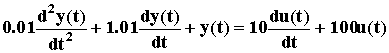Таким образом можно определить уравнение динамики реальных звеньев и всей реальной САУ, если оно теоретически это сделать затруднительно. Для снятия частотных характеристик реальной разомкнутой САУ на ее вход подают гармонический сигнал с изменяемой частотой и определяют изменение амплитуды и фазы выходного сигнала в зависимости от частоты. По полученным характеристикам определяют уравнение динамики, после чего САУ можно исследовать теоретически.

7.2. Законы регулирования

Пусть задана какая-то САР (рис.59).

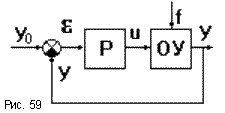
Законом регулирования называется математическая зависимость, в соответствии с которой у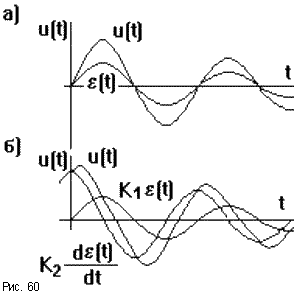 правляющее воздействие на объект вырабатывалось бы безынерционным регулятором.

Простейшим из них является пропорциональный закон регулирования, при котором

  u(t) = Ke(t) (рис.60а),

где u(t) - это управляющее воздействие, формируемое регулятором, e(t) - отклонение регулируемой величины от требуемого значения, K - коэффициент пропорциональности регулятора Р.

То есть для создания управляющего воздействия необходимо наличие ошибки регулирования и чтобы величина этой ошибки была пропорциональна возмущающему воздействию f(t). Другими словами САУ в целом должна быть статической.

Такие регуляторы называют П-регуляторами.

Так как при воздействии возмущения на объект управления отклонение регулируемой величины от требуемого значения происходит с конечной скоростью (рис.60б), то в начальный момент на вход регулятора подается очень малая величина e , вызывая при этом слабые управляющие воздействия u. Для повышения быстродействия системы желательно форсировать процесс управления.

Для этого в регулятор вводят звенья, формирующие на выходе сигнал, пропорциональный производной от входной величины, то есть дифференцирующие или форсирующие звенья.

Такой закон регулирования называется пропорционально - дифференциальным:

  u(t) = K₁e(t) + K₂ de(t)/dt.

В соответствии с ним работают ПД-регуляторы.

Чем быстрее нарастает отклонение регулируемой величины от требуемого значения, тем интенсивнее работает ПД-регулятор, что препятствует дальнейшему нарастанию данного отклонения. Кроме того при увеличении отклонения (de(t)/dt > 0) управляющий сигнал u будет больше, чем при уменьшении (de(t)/dt < 0), что также играет положительную роль, снижая колебательность процеса управления.

Добавление в регулятор двух дифференцирующих звеньев позволяет формировать управляющее воздействие по второй производной отклонения e , такой регулятор называется ПДД-регулятором.

Интегральный закон регулирования реализуется И-регулятором, его формулировка:

  .

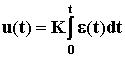Этот регулятор наращивает управляющее воздействие до тех пор пока управляемая величина отличается от требуемого значения, то есть пока e(t) 0.

И-регулятор обеспечивает астатическое регулирование.

При малых e управляющее воздействие изменяется с малой скоростью, поэтому данный регулятор очень инерционный.

Чтобы увеличить быстродействие обычно последовательно с ним включают усилитель, это дает пропорционально-интегральный закон регулирования (ПИ-регулятор), его формула:

  .

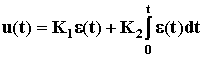Первое слагаемое обеспечивает быстродействие, второе - астатичность, то есть точность регулирования.

Еще большее быстродействие обеспечивается при добавлении слагаемого, пропорционального производной от отклонения управляемой величины de/dt, такой закон регулирования обеспечивается ПИД-регулятором, его формула:

 

.
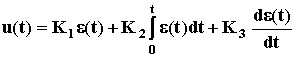