Лекция 3. Производная функции комплексного переменного.

Пусть задана однозначная функция в области D комплексной плоскости (z).

Определение. Производной от функции в точке z называется

(1)

когда этот предел существует и любым образом стремится к нулю.

Функция называется дифференцируемой в точке z, если в этой точке существует .

Определение. Функция называется аналитической в области D, если она дифференцируема в каждой точке области D и имеет в этой области непрерывную производную.

Теорема. Для того, чтобы функция была аналитической в области D, необходимо и достаточно, чтобы в каждой точке , функции и имели непрерывные частные производные, удовлетворяющие условиям Коши - Римана:

Производная находится по формулам

.

Из определения производной функции , которое аналогично определению производной функции действительного аргумента, следует, что правила дифференцирования и свойства аналитических функций аналогичны правилам дифференцирования и свойствам функции действительного аргумента.

Если - аналитические,

то также аналитические.

1.

2.

3.

Имеют смысл и производные высших порядков а также таблица производных элементарных функций.

1.	4.	7.
2.	5.	8.
3.	6.	9.

Пример. Доказать, что аналитическая во всей плоскости.

Решение.

Проверим условия Коши-Римана.

.

Вывод. Условия выполнены - аналитическая в плоскости (z).

Гармонические функции и их связь с аналитическими.

Определение. Функция называется гармонической, если она удовлетворяет уравнению Лапласа

Рассмотрим аналитическую функцию в области (z), тогда в этой области функции удовлетворяют условиям Коши – Римана

(1) (2)

Дифференцируем обе части равенства (1) по х, а (2) по y

и

так как смешанные производные равны, то приравниваем и получаем

а это значит, что действительная часть аналитической функции есть функция гармоническая. Аналогично, можно показать, что и мнимая часть аналитической функции также гармоническая. Их называют гармоническими сопряженными функциями.

Пример. Найти аналитическую функцию по известной ее действительной части , при условии .

Решение.

Используем условия Коши – Римана

- интегрируем по

.

С другой стороны

, найдем с.

.

Геометрический смысл модуля производной

Рассмотрим две комплексные плоскости (z) и (w) и, соответственно, области D (z) и G (w) .

Дадим геометрическое представление производной функции в точке , когда . Функция отобразит точку (z) в точку (w).

Рис.13

Кривую Г (z), функция отобразит в кривую Г₁ (w). По определению производной в точке это комплексное число. Запишем его в показательной форме

где (1).

Итак, или с точностью до бесконечно малых, имеем

, где расстояние между точками , а - расстояние между точками . Коэффициент указывает, в каком отношении в результате отображения изменяются линейные размеры, то есть .

Следовательно, величину естественно назвать коэффициентом искажения масштаба, причем, если K>1, т. е. , то коэффициент растяжения, если K<1, т. е. , то коэффициент сжатия в т. .

Вывод. Отображение, осуществляемое функцией , бесконечно малые круги (окрестности) преобразует в подобные же круги, сжатые или растянутые, т. е. обладают свойством постоянства.

Геометрический смысл аргумента производной.

Введем обозначения: - это углы секущих AB и A₁B₁ соответственно к осям Оx и Оu (рис.13);

углы касательных с осями ox и ou в точках к кривым Г и Г₁;

,

Находим

Вывод. Аргумент производной геометрически представляет собой разность между углами, образованными касательными к кривым Г и Г₁ в точках с осями соответственно ox и ou, т. е. - есть угол, на который поворачивается линия Г, проходящая через т. при отображении осуществляемом функцией .

Пример. Найти угол поворота и коэффициент искажения масштаба в т. при отображении .

Решение. Угол поворота , а коэффициент искажения масштаба в т. .

сжатие.

нет искажения.

Конформное отображение.

Пусть Г₁ и Г₂ – гладкие кривые, выходящие из точки (рис.14). Касательные к ним образуют углы соответственно . Образы этих кривых - кривые на плоскости (w), имеют касательные в точке w, образующие углы . Если то где угол между касательными к линиям Г₁ и Г_2, а - угол между линиями Г₁ и Г₂ и эти углы равны. Следовательно, при отображении, осуществляемом аналитической функцией , угол между двумя кривыми, пересекающимися в точке, остается без изменения. Это свойство носит название консерватизма углов.

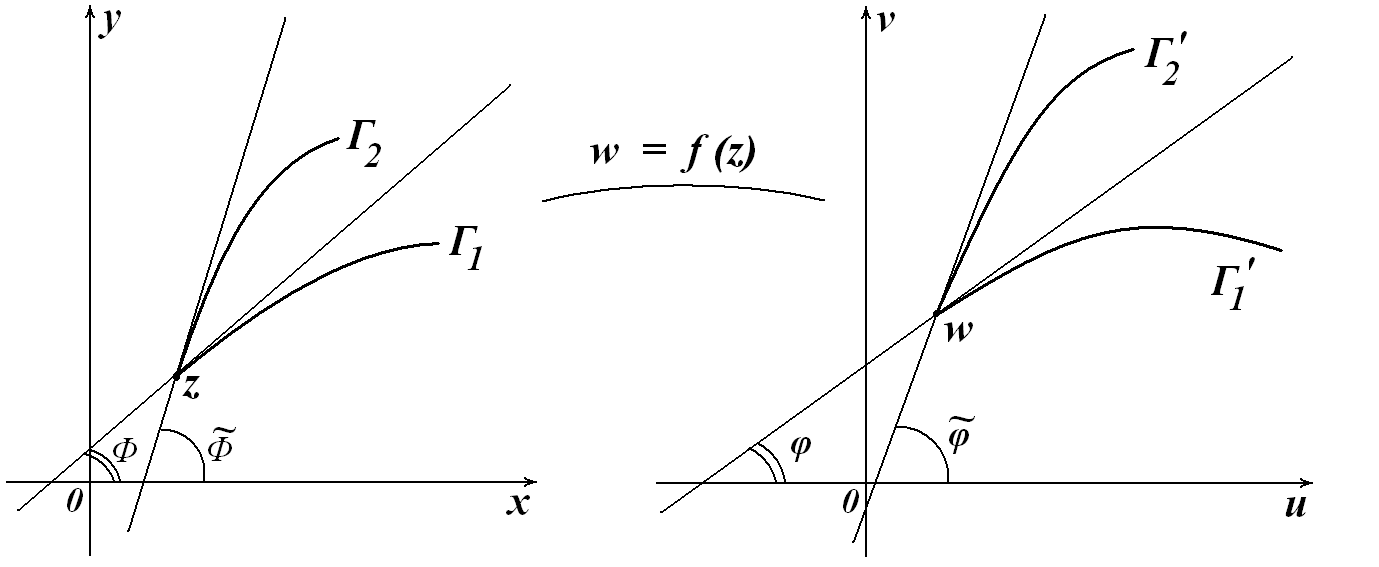
Рис.14

Определение. Отображение, обладающее свойством постоянства коэффициента растяжения и консерватизма углов, называется конформным отображением.

Таким образом, мы показали, что отображение, осуществляемое аналитической функции , является конформным во всех точках, где . Обратное утверждение также верно.

Пример. Каково отображение, осуществляемое функцией ?

Решение. Находим , во всех точках (z), следовательно, отображение - аналитическое и конформное во всей плоскости (z).

- растяжение в 2 раза,

поворота нет.