РЕЦЕНЗИЯ

на работу «Теория функций комплексного переменного»

Составители: Труппова В.А., Шульгина О.Н., Кочеткова О.Н., Морозова С.Г.

Работа содержит материал пяти лекционных занятий и четырех тем практических занятий по ТФКП. Данный раздел математики входит в государственный стандарт почти всех технических специальностей.

Аппарат ТФКП применяется при решении задач в гидро- и аэродинамике, теории упругости, радиотехнике и др.

Авторы изложили материал в краткой, но доступной для студентов форме, иллюстрируя его необходимыми примерами. В работе рассмотрены основные разделы ТФКП, которые необходимы студентам при выполнении курсовых и дипломных работ.

В практической части приведены примеры с решениями для аудиторных занятий, а также большой набор задач для самостоятельной и внеаудиторной работы студентов.

В имеющихся учебниках отсутствует сжатое изложение данного раздела. Авторы с успехом справились с этой задачей.

Работа будет полезна не только студентам, но и преподавателям.

Считаю, что данная работа соответствует современным методическим требованиям и должна быть опубликована.

Огнёв И.А. – к.ф.н., доцент каф. математики.

Предисловие.

Содержание этой работы основано на материале курса «Теория функций комплексного переменного», который читается авторами в течение ряда лет студентам технических специальностей ИрГТУ. Курс претерпел кардинальные изменения в связи с уменьшением часов отводимых на специальные разделы математики. Тем не менее, необходимо за несколько лекций ознакомить студентов с основами теории и научить их пользоваться аппаратом функций комплексного переменного для решения конкретных задач, которые возникают в гидро- и аэродинамике, теории упругости, электродинамике, радиотехнике.

«Образование – это то,

что остается, когда все

выученное забывается».

А. Лауэ.

Лекция 1. Понятие комплексного числа и действия над комплексными числами.

Понятие комплексного числа возникло в первую очередь в результате потребностей автоматизации вычислений. Даже простейшие алгебраические операции над действительными числами выводят за пределы области действительных чисел. Так, например, решение простейшего уравнения х²+1=0 не может быть разрешено в действительных числах, так как .

Тем самым надо или отказаться от автоматического применения установленных методов решения и каждый раз проводить подробное исследование возможности их применения, или расширить область действительных чисел с тем, чтобы основные алгебраические операции всегда были выполнимы. Таким расширением области действительных чисел являются комплексные числа.

1. АЛГЕБРАИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА.

Определение 1. Комплексным числом называется двучлен вида

(1)

где: x и y – действительные числа, i – const, такое, что

,

- действительная часть комплексного числа.

- мнимая часть комплексного числа.

Два комплексных числа называются равными, когда равны их действительные и мнимые части.

Если , то при .

Комплексное число называется сопряженным комплексному числу .

Сумма комплексных чисел есть комплексное число:

.

Произведение комплексных чисел есть комплексное число:

.

Отношением комплексных чисел является комплексное число:

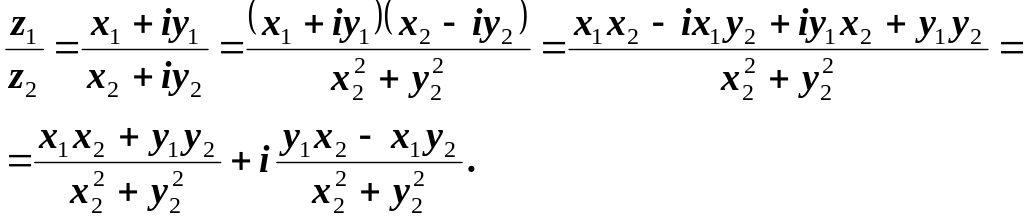
II.ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА

Каждому комплексному числу поставим в соответствие точку с координатами (x,y) на плоскости R². Это соответствие взаимно однозначное и называется геометрической интерпретацией комплексного числа.

М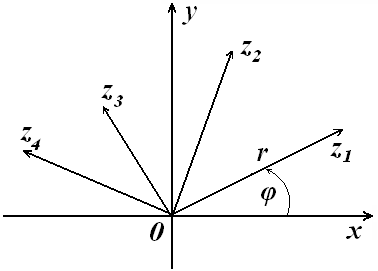 ножество точек образует ком­плексную плоскость, кото­рую будем обозначать (z). Точки z - это концы векторов, проведен­ных из начала координат.

Как и вектор, комплексное число можно определить с помощью угла и длины вектора, , т.е., аргумента и модуля Рис.1 Комплексная плоскость. (радиуса).

с точностью до ,

Т

Рис.1.

ак как

, (2)

то

; ;

где – главное значение аргумента z, удовлетворяющее условиям

или .

Из рисунка 1 следует, что , причем при

Для значения аргумент не определен.

Используя формулы (2), запишем

,

- тригонометрическая форма комплексного числа. (3)

Действия над комплексными числами в тригонометрической форме.

Даны два комплексных числа

.

1. Умножение

,

т. е.

Если имеется n одинаковых сомножителей , то

- формула Муавра. (4)

2) Деление

То есть

3) Извлечение корня n-й степени из комплексного числа.

О

пределение 2. Корнем n-ой степени из комплексного числа z называется такое число , что (5)

Обозначим

возведем в n-ю степень по формуле Муавра.

.

Комплексные числа равны, если равны их модули и аргументы, поэтому

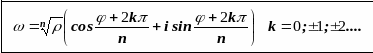(6)

Пример 1. Вычислить

3. ПОКАЗАТЕЛЬНАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА.

Любое комплексное число можно записать в показательной форме

(7)

Эта форма комплексного числа получается, если применить формулу Эйлера

(8)

В показательной форме удобно производить действия:

Пример 2. Записать в показательной форме число

,

.