
- •VI. Література.
- •ViІ.Запитаня для контролю і самоконтролю.
- •Лабораторна робота № 9 Зняття кривої намагнічування та петлі гістерезису за допомогою осцилографа
- •IV. Теореттичні відомості та опис установки.
- •V. Завдання та хід виконання роботи.
- •VI.Література.
- •Лабораторна робота № 10 Вимірювання потужності змінного струму та зсуву фаз між струмом і напругою
- •V. Завдання та хід виконання роботи
- •Визначення коефіцієнта потужності змінного струму.
- •2. Визначення зсуву фаз між струмом і напругою у колах змінного струму з різним характером навантаження.
- •VI. Література
- •VII. Запитання для самоконтролю і контролю
- •Ііі. Теоретичні питання програми, знання яких необхідне для виконання роботи
- •IV. Теоретичні відомості та опис установки
- •V. Завдання та хід виконання роботи
- •VI. Література
- •VII. Запитання для самоконтролю і контролю
- •Лабораторна робота №12 вивчення роботи і зняття статичних характеристик напівпровідникових діода та Транзистора
- •IV. Теоретичні відомості та опис установки.
- •V. Завдання.
- •Vі. Література
- •Vіі. Запитання для самоконтролю і контролю
V. Завдання та хід виконання роботи
а). Вимірювання індуктивності котушки.
Із формули (11.12) випливає, що індуктивність котушки:
![]() ,
(11.15)
,
(11.15)
де
![]() ,
(11.16)
,
(11.16)
а активний опір
активний опір
![]() .
(11.17)
.
(11.17)
1. Збирають електричне коло за схемою, поданою на рис. 11.1 (Реостат r відіграє тут роль тільки запобіжника).
2. Для визначення активного опору Rа з’єднують за допомогою ключа К коло котушки з джерелом постійного струму і вимірюють амперметром та вольтметром Іпост та Uпост.
3. Вимірювання проводять ще для шести значень напруги; дані заносять у таблицю 11.1.
4. Розраховують Rа для кожного рядка таблиці 11.1 за формулою (11.17), проводять обробку даних за програмою 1 (додаток 3) і записують остаточний результат
![]() =
<
>
± ∆
.
=
<
>
± ∆
.
5. Для знаходження сумарного опору Z1 кола з’єднують його ключем К з джерелом змінного струму і вимірюють вольтметром та амперметром Іеф.та Uеф.
Tаблиця11.1
№ п/п |
Uпост. |
Іпост |
|
Α |
tα,n |
S< |
∆ |
E |
||
поділки |
В |
поділки |
А |
Ом |
- |
- |
Ом |
Ом |
% |
|
|
|
|
|
|
|
|
|
|
|
|
для сімох напруг. Дані заносять у таблицю 11.2.
За формулами (11.16) і (11.15) обчислюють сумарний опір Z1 кола та індуктивність котушки L за програмою 1 (додаток 3), і записують остаточний результат
L = <L> ± ∆L.
Таблиця 11.2
№ п/п |
|
Uеф |
Іеф |
|
|
α |
tαn |
S<L> |
∆L |
EL |
||
Ом |
под |
В |
под |
А |
Ом |
Гц |
- |
- |
Гц |
Гц |
% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. Циклічну частоту ω (для таблиці 11.2) обчислюють за формулою ω=2πυ, де лінійна частота змінного струму υ=50 Гц.
8. Роблять висновки за результатами таблиць 11.1 та 11.2.
б). Визначення ємності конденсатора.
Ємність конденсатора С може бути визначена за формулами (11.13)
 ,
(11.18)
,
(11.18)
де
![]() - сумарний опір кола;
- сумарний опір кола;
![]() (11.18’)
(11.18’)
Rа – омічний (активний) опір кола;
ω – циклічна частота.
Остання
формула значно спрощується, якщо
![]() вимірюється
безпосередньо на обкладках конденсатора,
бо тоді омічний опір практично рівний
нулеві (при виключеному магазині опорів
(рис.11.1)). В цьому випадку
вимірюється
безпосередньо на обкладках конденсатора,
бо тоді омічний опір практично рівний
нулеві (при виключеному магазині опорів
(рис.11.1)). В цьому випадку
![]() .
(11.19)
.
(11.19)
1. Замість котушки вмикають у коло (рис. 11.1) досліджуваний конденсатор.
2. Замикають перемикач на змінний струм і за амперметром і вольтметром вимірюють струм і напругу. Дані заносять у таблицю 11.3.
3. Змінюючи , вимірювання повторюють сім разів. Для збільшення точності вимірювання покази приладів повинні бути у другій половині шкали.
4. Частота ω, як і раніше, рівна ω=2πυ=314 с-1.
5. Для кожного рядка таблиці 11.3 розраховують повний опір Z2 та ємність конденсатора С за формулами (11.18’) та (11.19).
6. Проводять статистичну обробку даних для С за програмою 1 (додаток 3);і записують остаточний результат:
С = <С> ± ∆С.
7. Роблять висновок з проведеного дослідження ємності конденсатора.
Таблиця 11.3
№ п/п |
ω |
Uеф. |
Іеф. |
|
С |
α |
tαn |
S<С> |
∆С |
EС |
||
Гц |
под |
В |
под |
А |
Ом |
Ф |
- |
- |
Ф |
Ф |
% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в). Перевірка закону Ома для кола змінного струму.
Якщо в коло змінного струму увімкнені послідовно омічний (активний) опір, індуктивність та ємність, то повний опір кола (імпеданс) визначається за формулою
![]() .
(11.20)
.
(11.20)
Активний опір (омічний) Rа не зміщує фази струму відносно фази напруги (формули (11.1), (11.2)). За допомогою векторної діаграми це зображують так (рис.11.2):
 І
U
І
U
Рис.11.2
Як
видно з формули (11.3) напруга у колі
змінного струму при Rа
→0 (формула 11.5) tgφ→∞
і φ=90˚ (рис.11.3).


UL
І
Рис.11.3
Аналогічно для конденсатора можна прийти до висновку (формули (11.6) і (11.8)), що в ньому напруга відстає від струму на величину фази φ=90˚ при (Rа =0) (рис.11.4).


І
UС
Рис.11.4
Зсув фази між струмом і напругою у колі змінного струму легко визначити з так званої векторної діаграми кола.
Нехай коло складається з послідовно з’єднаних резистора, котушки і конденсатора (рис. 11.5). Причому котушку будемо вважати ідеальною, тобто, такою,


Рис.11.5.
що не має омічного опору. Її омічний опір виділимо окремо як активний опір кола Rа.
Побудову векторної діаграми розпочинають з вибору напрямку осі струму, наприклад, горизонтальною, як показано на рис.11.6.
Падіння напруги в активному опорі Uа відкладають вздовж осі І , бо φ=0.
Падіння напруги в UL відкладають під кутом 90˚ до напрямку І (в бік випередження), а UС - під кутом 90˚ до напрямку І у бік відставання.
 UL
UL

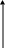



U
U L-
UС
L-
UС


 φ
Uа
І
φ
Uа
І
UС
Рис.11.6
Довжини
векторів Uа,
UL
та
UС
для даної
сили струму визначаються відповідними
– активним Rа,
індуктивним RL=ωL
та ємнісним
![]() - опорами.
- опорами.
Далі геометрично додають вектори Uа, UL та UС.
Спочатку зручніше додати вектори UL та UС, оскільки вони лежать на одній прямій. Потім, додають UL -UС з Uа і отримують вектор U, величина і напрямок (зсув фаз) якого визначаються з діаграми.
З рисунка 11.6 за теоремою Піфагора:
U2= Uа2+( UL -UС)2 або (ІZ)2=(І Rа)2+І2·(RL -RС)2
звідки
![]() (11.20)
(11.20)
Перевірка справедливості цієї формули і є метою даного завдання.
1. Вмикають в коло котушку індуктивності і послідовно з нею конденсатор. Омічний опір котушки індуктивності, її індуктивність та ємність конденсатора були визначені у завданнях а), б).
2. Замикають перемикач на змінний струм, і вимірюють Uеф. та Іеф. сім разів, змінюючи лабораторним автотрансформатором Uеф.
3.
Дані заносять у таблицю 11.4,
і для кожного її рядка обчислюють повний
опір кола за формулою:
![]()
Таблиця 11.4
№ п/п |
|
Uеф |
Іеф |
|
<Z> |
α |
tαn |
S<Z> |
∆Z |
EZ |
||
Ом |
под |
В |
под |
А |
Ом |
Ом |
- |
- |
Ом |
Ом |
% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Проводять статистичну обробку результатів за програмою 1 (додаток 3) і записують остаточний результат
Z = <Z> ± ∆Z.
5. Знаючи ω, С, L, Ra, розраховують Z за теоретичною формулою (11.20), і проводять порівняння результату, одержаного експериментально, та розрахованого теоретично. Роблять висновок.
