ЛАБОРАТОРНА РОБОТА № 7

ВИЗНАЧЕННЯ ПИТОМОГО ЗАРЯДУ ЕЛЕКТРОНА

“ МЕТОДОМ МАГНЕТРОНА ”

І. МЕТА РОБОТИ: вивчення дії електричного і магнітного полів на рухомий

електричний заряд та дослідне визначення відношення “методом магнетрона”

ІІ. ДЛЯ РОБОТИ ПОТРІБНІ: електронна лампа з циліндричним анодом, соленоїд, міліамперметр, вольтметр, амперметр, реостати, джерело напруг типу УИП-1, вимикачі.

ІІІ. ТЕОРЕТИЧНІ ПИТАННЯ ПРОГРАМИ, ЗНАННЯ ЯКИХ

НЕОБХІДНЕ ДЛЯ ВИКОНАННЯ РОБОТИ:

1. Напруженість електричного поля. Поле точкового заряду. Однорідне електричне поле.

2. Сила, що діє на електричний заряд в електричному полі.

3. Сила, що діє на рухомий електричний заряд в магнітному полі.

ІV. ТЕОРЕТИЧНІ ВІДОМОСТІ ТА ОПИС УСТАНОВОК:

1. Заряд електрона е = -1,610^-19 Кл та його маса m= 9,1  10^-31 кг входять до числа фундаментальних сталих фізики. Однак у багатьох фізичних явищах немає потреби визначати абсолютні значення е і m, бо основну роль в них відіграє відношення електрона до його маси, тобто так званий питомий заряд . Знайти цю величину важливо як з теоретичного погляду (зокрема при вивченні внутрішньої будови речовини), так і з практичного (при застосуванні електронно-променевих трубок тощо).

2. Існує багато різноманітних методів визначення відношення . Значна частина їх грунтується на використанні дії електричного і магнітного полів на рухомий електричний заряд.

На заряд q , що рухається зі швидкістю в магнітному полі з індукцією , діє сила Лоренца,

= q[ ], (7.1)

модуль якої

F=qvBsin (7.2),

де ­­ – кут між векторами і .

Для електрона q=е і тому

= е[ ] (7.1')

та

F=еvBsin (7.2').

Проте слід звернути увагу на те, що в формулі (7.1') напрямок векторного добутку [ ] змінюється на протилежний внаслідок його множення на від’ємний заряд електрона .

Якщо  , то sin =1 і тоді сила Лоренца

F=еVB (7.2'').

В загальному випадку, коли на рухомий заряд одночасно діють електричне поле напруженістю та магнітне поле з індукцією , результуюча сила становитиме геометричну суму прискорюючої дії електричного поля е в напрямі – і відхиляючої дії магнітного поля е[ ]:

= е + е[ ] (7.3)

Строго кажучи „силою Лоренца ” називають силу, визначену за формулою (7.3).

3. Для чіткого розуміння процесів, які мають місце у вакуумних електронних лампах , нагадаємо, що згідно з формулою

= е (7.4)

рух електрона сповільнюється, коли той рухається вздовж силових ліній електричного поля і прискорюється , коли він рухається проти силових ліній цього поля (мал. 7.1):

e

< Мал. 7.1. >

4. Якщо електрон рухається у перпендикулярному магнітному полі (  ) , то згідно з векторним добутком (7.1') він відхилявся б у напрямку [ ] , але від’ємний знак заряду електрона (е<0 ) змінює цей напрямок на протилежний; в підсумку, на електрон діє сила в напрямку е[ ].

5. Метод вимірювання , застосований у даній роботі називають „ методом магнетрона ” у зв’язку з тим, що застосована тут конфігурація електричного і магнітного полів дуже нагадує конфігурацію полів у магнетронах – генераторах електромагнітних коливань в області надвисоких частот (НВЧ).

Р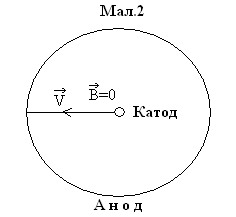 ух електронів у цьому випадку відбувається в кільцевому просторі між катодом і анодом двоелектродної електронної лампи.

Нитка розжарення лампи (катод) розташований вздовж осі циліндричного анода. Силові лінії електричного поля спрямовані радіально від додатнього електрода – анода до катода.

При відсутності магнітного поля електрони, що вилітають з катода внаслідок явища термоелектронної емісії , рухаються по прямолінійних траекторіях від катода до анода, тобто вздовж радіусів (мал. 7.2)

Для створення і області між катодом і анодом магнітного поля електронну лампу розташовують так, щоб її нитка розжарення (катод) була віссю соленоїда . Відомо, що соленоїд створює магнітне поле з силовими лініями індукції паралельними його осі. Отже, за такої конструкції установки і будуть взаємно перпендикулярними.

Напруженість електричного поля спрямована по радіусу в напрямку до катода, а індукція магнітного поля паралельна дротині катода лампи. Як видно з формули (1') сила Лоренца завжди перпендикулярна до на-

Рис. 7.2 прямку руху електрона , тому вона не виконує роботи : бо не змінює величини вектора швидкості ; проте вона змінює напрямок вектора .

При деякій достатній величині індукції магнітного поля траєкторія руху електрона перестає вже навіть торкатися анода, тобто електрони не будуть попадати на анод. Отже, критичною індукцією є така індукція магнітного поля, при якій траєкторії руху електронів будуть замкненими на катод (мал. 7.3, крива 1). При будь-якій іншій індукції магнітного поля, котра менша від критичної, електрони будуть мати траекторії, що починаються на катоді і закінчуються на аноді (наприклад,

крива 2, мал.7.3). Нарешті, із посилен-

ням магнітного поля при > згідно

з (7.1') сила, що діє не електрони, буде

зростати і криві (траекторії) руху елект-

ронів будуть дедалі меншого радіуса (7.5)

Таким чином, сила Лоренца відіграє

роль доцентрової сили

(7.6)

Рис. 7.3 Вважаючи (в першому наближенні), що при = траєкторія руху електронів є коловою (мал. 7.3, крива 1) з радіусом , знайдемо з рівності (7.6) шукане відношення:

(7.7)

Швидкість електронів можна визначити з рівності кінетичної енергії електронів, роботи їх прискорення в електричному полі лампи

(7.8)

Тут U_A – різниця потенціалів (напруга) між анодом і катодом. З формули (7.8) : . (7.9)

Підставивши (7.9) у (7.7), одержимо:

. (7.10)

Крива залежності струму в електронній лампі від індукції магнітного поля при сталому струмі розжарення катода і сталій анодній напрузі U_A в ідеальному випадку виражається пунктирною кривою 1 (мал. 7.4).

В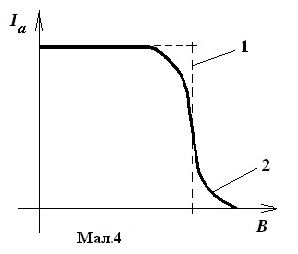 наслідок того, що електрони, які рухаються від катода до анода, мають різні швидкості, зменшення анодного струму відбувається поступово

(крива 2 на мал. 4); повільніші електрони перестають попадати на анод при меншому значенні індукції магнітного поля , ніж більш швидкі.

Якщо знімати криві І _а = f(B) при різних значеннях анодної напруги U_A, одержимо сім’ю кривих для різних .

Рис. 7.4 Однак, при знятті цих кривих напруга розжарення катода повинна бути однаковою. Криві І _а = f(B) ще називають скидними характеристиками лампи.

У даній роботі замість діодів з циліндричним анодом можна використовувати тріод з таким самим анодом, наприклад, лампу 6С5С. Щоб третій електрод тріода – сітка не спотворювала результатів вимірювання , її сполучають з анодом через великий опір (десятки тисяч омів). Як уже згадувалось вище, магнітне поле створюється за допомогою соленоїда , довжина якого значно більша діаметра. Тоді можна вважати, що в середній частині соленоїда магнітне поле буде однорідним, а його індукцію знаходять за формулою:

, (7.11)

де μ – відносна магнітна проникність середовища (в нашому випадку повітря);

μ₀ – магнітна стала , яку називають абсолютною магнітною проникністю вакууму

( );

І_с – сила стуму в обмотці соленоїда ( в амперах);

n – число витків, що припадають на одиницю довжини соленоїда (для даного соленоїда n=8·10³  ).

Соленоїд живиться від джерела постійного струму , наприклад, ВСА-5К.

Струм в соленоїді будемо вважати критичним І_кр при В=В_кр . Тоді врахувавши (7.11). Остаточно одержимо таку робочу формулу:

(7.12)

Отже, для визначення питомого заряду електрона „методом магнетрона”, необхідно знати радіус r_A анода лампи (для даної лампи r_A=9,6 мм), число витків соленоїда n на одиницю довжини, анодну напругу U_A та I_{c кр} , що знаходиться з I_A = f( I_c) , подібного до графіка I_A = f(В), наведенного на мал. 7.4.

V. ЗАВДАННЯ ТА ХІД ЙОГО ВИКОНАННЯ

Визначити питомий заряд електрона

1. Збирають установку за схемою, поданою на рис.7.5.

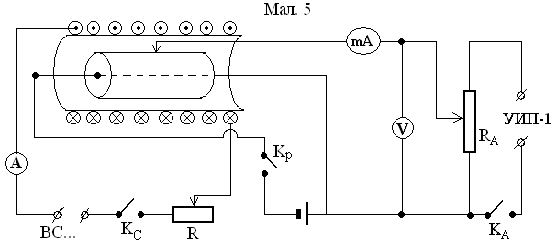
Рис. 7.5

2. Ставлять контакт потенціометра R_A в положення, при якому U_A = 0 і вмикають коло розжарення.

3. Замикають коло анода (ключем К_а) і за допомогою потенціометра R_A установлюють одну з напруг U_A , наприклад, 100 В і переконуються в тому, що величина анодного струму припадає на другу половину шкали міліамперметра.

4. Увімкнувши максимальний опір R , замикають коло соленоїда (ключа К_С) і міліамперметром вимірюють силу анодного струму.

5. Збільшують силу струму в соленоїді І_С в межах від 0 до максимального і вимірюють залежність I_а = f( I_С ) . Дані заносять у таблицю 7.1.

Таблиця 7.1

ІС, А	0	0,1	0,2	0,3	………
Іа, мА
∆ Іа, мА

IC , А	0	0,1	0,2	0,3	..........
Іа , мА
∆ Іа , мА

6. Ставлять R_С у вихідне положення , при якому І_С = 0, розмикають коло соленоїда і повторюють вимірювання при інших значеннях анодної напруги U_A . Дані заносять у таблиці 7.1, 7.1', 7.2'' ..., аналогічні таблиці 7.1'.

7. За даними таблиць 7.1, 7.1', 7.2'', ... будують скидні характеристики при різних U_A , з яких методом диференціювання кривої знаходять залежності ∆І_А = f( I_C), їх будують на фоні скидних характеристик.

8. За максимумами залежностей ∆І_А = f( I_C) з графіків визначають І_{с кр} , І'_{С кр}, І''_{С кр} ... . Дані заносять у таблицю 7.2

9. Для кожного рядка таблиці 2 розраховують за формулою (7.12) і проводять статистичну обробку даних за програмою 1 (додатки 2 і 3).

10. Записують остаточний результат:

=

і роблять висновок про якість проведених вимірювань (наприклад, на скільки % відрізняється одержаний результат від табличного значення –

Таблиця 7.2

№ п/п	UА	ІІскр	р	и	t, n		S< >		E
	В	А	м						%
1. 2. 3. …

VI. ЛІТЕРАТУРА

[1] – стор. 331, 336–337, 396–401. [5] – стор. 312–316, 368–378.

[2] – стор. 13–17, 161–165. [7] – стор. 184–189.

[3] – стор. 16–20, 208–217. [8] – стор. 321–324.

[4] – стор. 116–118, 223–225. [9] – стор. 96–99.

.

VII. ЗАПИТАННЯ ДЛЯ САМОКОНТРОЛЮ І КОНТРОЛЮ

1.За законом збереження енергія замкненої системи зберігається. А у яких випад-

ках енергія системи змінюється? Яка причина зміни кінетичної енергії заряду,що

рухається в електростатичному полі?

2.Чи змінюється енергія заряду, який влітає у магнітне поле:

–вздовж силових ліній цього поля?

–перпендикулярно до силових ліній магнітного поля? Поясніть відповідь.

3.Дайте визначення основного закону динаміки обертального руху. Зробіть малю-

нок, на якому зазначте напрямки векторів моменту імпульсу електрона, що руха-

ється по колу в магнітному полі, та моменту сили Лоренца.

4.Як треба змінити описаний у цій роботі метод для визначення відношення заря-

ду до маси для протона? Чи можна застосовувати цей метод для визначення хара-

ктеристик нейтрона? Відповідь обґрунтуйте.

5.Як рухається електричний заряд в однорідному магнітному полі, коли кут між

напрямком вектора швидкості заряду і напрямком вектора магнітної індукції до-

рівнює: 0; /2; довільній величині?

6.Пояснити принцип дії магнетрона.

7.Намалювати траєкторії руху електрона у магнітному полі для випадків:

1) В < В_кр ; 2) В = В_кр; 3) В > В_кр.

ПРОТОКОЛ 7

ВИЗНАЧЕННЯ ПИТОМОГО ЗАРЯДУ ЕЛЕКТРОНА “ МЕТОДОМ МАГНЕТРОНА ”

Заряд електрона е = -1,610^-19 Кл та його маса m= 9,1  10^-31 кг входять до числа фундаментальних сталих фізики. Однак у багатьох фізичних явищах немає потреби визначати абсолютні значення е і m, бо основну роль в них відіграє відношення заряду електрона до його маси, тобто так званий питомий заряд . Знайти цю величину важливо як з теоретичного аспекту (зокрема при вивченні внутрішньої будови речовини), так і з практичного (при застосуванні електронно-променевих трубок тощо).

Існує багато різноманітних методів визначення відношення . Значна частина їх грунтується на використанні дії електричного і магнітного полів на рухомий електричний заряд. На заряд q , що рухається зі швидкістю в магнітному полі з індукцією , діє сила Лоренца, В загальному випадку, коли на заряд діють електричне і магнітне поля, сила Лоренца має вигляд:

F_л=qE+qVB sin (1)

У більшості випадків під силою Лоренца розуміють силу, яка дії на заряд q при його русі в магнітному полі з індукцією В :

F_л=q V B sin (2)

В простому магнетроні рух електронів відбувається в просторі між катодом і анодом двоелектродної електронної лампи. При цьому нитка розжарення лампи (катод) розташована вздовж осі циліндричного анода. Силові лінії електричного поля спрямовані радіально від катода до анода, рис.1.

П ри відсутності магнітного поля, електричне поле прискорює електрони, що емітували з катода (внаслідок термоелектронної емісії), в напрямку до анода, по силових лініях електричного поля.

Якщо вказану лампу помістити в магнітне поле так, щоб його силові лінії були паралельними катоду (перпендикулярно до площини рисунку), то електрони не зможуть рухатися до анода вздовж радіусів, оскільки на них буде діяти сила Лоренца

F_л = e V B sin, (3)

де е – заряд електрона.

Рис.1.

Тепер електрони будуть рухатися по траєкторіях, близьких до кругових, рис.2. Спочатку, при заданому електричному полі і малих значеннях індукції В, радіус траєкторії буде великим, і електрони будуть потрапляти на анод, крива 2 на рис.2. В анодному колі буде фіксуватися електронний струм І_а. При певному (критичному) значенні індукції В_кр сила Лоренца зменшить радіус траєкторії електронів, траєкторія стане круговою (крива 1 на рис.2), внаслідок чого електрони не потраплять на анод, струм в анодному колі зменшиться до нуля.

Насправді траєкторія руху електронів у випадку схрещених електричного і магнітного полів є складною, оскільки швидкість електронів змінна – спочатку маємо випадок рівноприскореного руху, а після повороту електронів в сторону катода, вони потрапляють в тормозне для них електричне поле, і рух становиться рівносповільненим. Тим не менше, для оцінки ситуації будемо вважати, що електрони рухаються по круговій траєкторії зі сталою кутовою і лінійною швидкостями, тобто V=const.

Рис.2.

При рівномірному обертовому русі сила Лоренца грає роль доцентрової сили, F_л=F _доц., або ж::

(4)

При В=В_кр радіус r дорівнює половині віддалі r_А, - віддалі від катода до анода, рис.2:

r=r_A/2 (5)

Із (4) і (5) знаходимо відношення e/m:

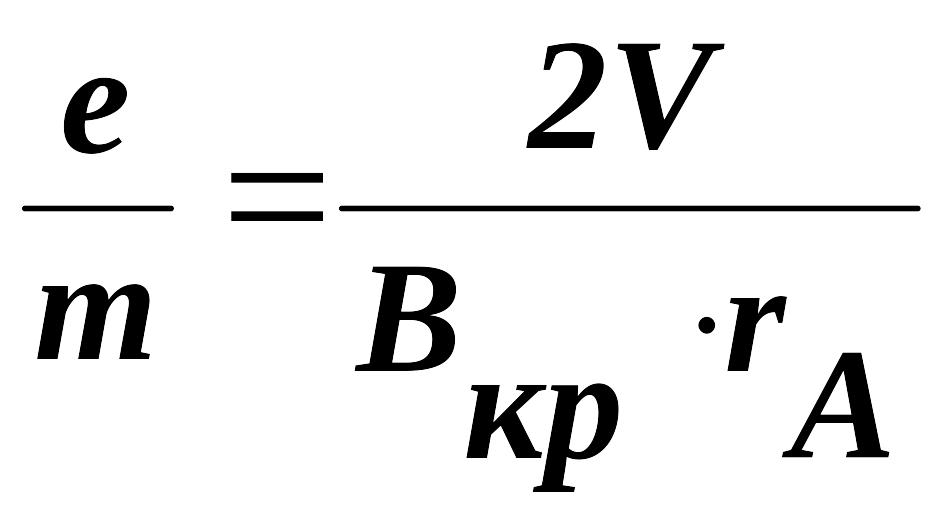(6)

В цій формулі треба визначити швидкість електронів V і критичне значення В_кр. При проходженні електричного поля від катода до анода електрони здобудуть енергію eU_A

де U_A – різниця потенціалів між катодом і анодом (в роботі вимірюється вольтметром). Ця енергія дорівнює кінетичній енергії електронів

(7)

(8)

Підставивши (8) в (7) і піднісши до квадрату, отримаємо:

(9)

В даній лабораторній роботі магнітне поле створюється за допомогою соленоїда, довжина якого значно більша діаметра. Тоді можна вважати, що в середній частині соленоїда магнітне поле є однорідним, а його індукцію можна знайти по формулі

, (10)

де μ – відносна магнітна проникність середовища (в нашому випадку повітря);

μ₀ – магнітна стала , яку називають абсолютною магнітною проникністю вакууму

( );

І_с – сила стуму в обмотці соленоїда ( в амперах);

n – число витків, що припадають на одиницю довжини соленоїда (для даного соленоїда n=8·10³  ).

Рис.3.

Критичне значення магнітної індукції В_кр можна знайти із графіка залежності анодного струму І_а від струму І_с в обмотці соленоїда – знайти значення І_с при найкрутішому ході графіка, рис.3. Отримане значення І_с підставити в (10), а (10) підставити в (9), отримаємо:

(11)

Нагадаємо, що величини n і r_A – це конкретні характеристики установки (інформацію про них брати у лаборанта).

ХІД РОБОТИ

1. Зібрати установку по схемі рис.4.

Рис.4.

2. Включити підігрів катода, ключ К_р.

3. Включити блок живлення анода, замкнути анодне коло, ключ К_а. Встановити анодну напругу 100 В, по вольтметру V.

4. Включити блок живлення соленоїда, поставити реостат R в максимальне положення, замкнути коло соленоїда ключем К_с.

5. Змінюючи реостатом R величину струму соленоїда І_с (виміряти амперметром А) зняти залежність анодного струму І_А (міліамперметром mA) від струму соленоїда І_с. Дані занести в таблицю. Побудувати графік

I_a=f (I_c).,

Знайти з графіка І_{с кр} , підставити його в формулу (11), знайти відношення e/m.

Запитання

1.Показати на схемі установки катодне коло.

2.Показати анодне коло, пояснити, від чого залежить величина анодного струму. Пояснити, що таке термоелектронна емісія.

3.Показати коло соленоїда. Нарисувати силові лінії магнітного поля соленоїда.

4.Пояснити, чим відрізняється робота опору R від роботи опору R_A.

5.Що буде, якщо довжина лампи і соленоїда одинакові? Якщо довжина соленоїда буде меншою від довжини лампи?

ЛАБОРАТОРНА РОБОТА № 8

Дослідження затухаючих коливань в LC-контурі за допомогою

осцилографа.

І. МЕТА РОБОТИ: вивчення впливу параметрів L, C та R на період коливань і швидкість їх затухання

ІІ ДЛЯ РОБОТИ ПОТРІБНІ: осцилограф, катушка індуктивності, конденсатор змінної ємності , генератор імпульсів, магазин опорів, зєднувальні проводи.

ІІ. Теоретичні питання знання яких необхідні для виконання роботи:

1. Коливальний контур. Власні електричні коливання. Частота і період коливань.

2. Згасаючі електричні коливання. Частота і період згасаючих електричних коливань. Логарифмічний декркмент згасання.

ІІІ. ТЕОРЕТИЧНІ ВІДОМОСТІ та опис установки: Електричні коливання можуть виникати у колі, що складається з індуктивнісі (L) , ємністі (C) та активного опіру (R). Таке коло називають коливальним контуром. Спочатку розглянемо ідеалізований коливальний контур (Рис.8.1) у якому вся ємність зосереджна в конденсаторі, індуктивність Р у котушці, а активний омічний опір рівний нулю.

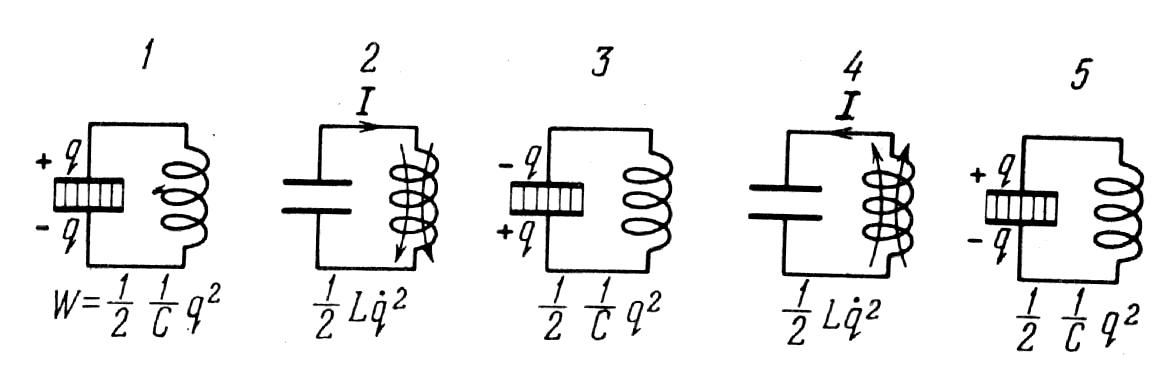
Рис 8.1.

Для збудження у контурі електричних коливань необхідно попередньо зарядити конденсатор . Тоді у початковий момент часу t₀ (рис. 8.1 а) вся енергія буде зосереджена в електричному полі конденсатора. Вона рівна , де q заряд однієї пластинки конденсатора. С – ємність конденсатора. В момент часу t₀ напруженість електричного поля в конденсаторі буде мексимальною (Е=Е_max). Далі конденсатор почне розряджатися. У контурі появиться зростаючий у часі струм І. В результаті енергія електричного поля буде зменшуватися, але зате виникне і буде зростати магнітне поле, що обумовлене струмом який протікає через котушку індуктивності. Енергія магнітного поля рівна , де L – індуктивність котушки, І – струм у котушці.

У деякий момент часу t₁ конденсатор повністю розрядится (рис 8.1 б), енергія електричного поля стане рівна нулю , а енергія магнітного поля в котушці досягне максимального значення. У наступний момент часу (рис 8.1б) магнітне поле котушки почне зменшуватися, в наслідок чого в ній індукується струм, який за правилами Ленца тече в тому ж напрямку, в якому протікає струм розряду конденсатора: конденсатор буде перезаряджатися. Коли заряди на пластинах конденсатора досягнуть початкового значення q сила труму стане рівна нулю. Після цього процеси у контурі протікають у зворотньому напрямку(рис 8.1г, 8.1д)., внаслідок чого система повертається у початковий стан, (рис 8.1а). і весь цикл повторюється знову і знову. У ході описаного процесу періодично міняються (тобто коливаються) заряд q на обкладках конденсатора, напруга U на конденсаторі та сила струму I, що протікає через індуктивність. Коливання супроводжується взаємним перетвореням енергії електричного і магнітного полів. Під час коливань зовнішня напруга до контуру не прикладена тому, за балансом напруг у контурі

.

Поділивши цей вираз на L, та замінивши через , одержимо наступне рівняння

Якщо ввести позначення , то попереднє рівняння матиме такий вигляд або .

Це - лінійне однорідне рівняння другого порядку, що одержало назву диференціального рівняння гармонічного осцилографа. Його розв’язками є функції (рис 8.1). Таким чином заряд на обкладках конденсатора змінюється за гармонічним законом з циклічною частотою . Що називається власною частотою коливань. Оскільки , то для періоду коливань, одержуємо так звану формулу Томсона

. (8.3)

Проте всякий реальний контур має активний опір тому енергія, що нагромаджена у контурі поступово втрачається на нагрівання цього опору, внаслідок чого вільні коливання згасають. Баланс напруг у такому контурі можна записати так :

Поділивши кожен член цього рівняння на L, вівши позначення і та врахувавши, що , одержимо

або

Розв’язком цього однорідного диференціального рівняння при умові, що , буде вираз (8.4), де частота коливань

.

Графік функції q=f(t) приведений на рис. 8.2.

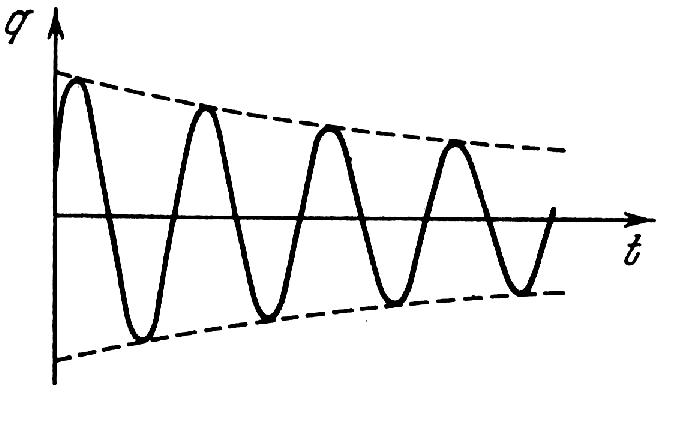
рис. 8.2

Графіки для напруги і сили струму мають аналогічний вигляд. Згасання коливання прийнято характеризувати логарифмічним декрементом згасання

, (8.6)

де А(t) та А(t+Т) амплітуди двох послідовних коливань відповідної величини у момент часу t та через період.

Легко перевірити, що логарифмічний декремент згасання за величиною обернений числу коливань N_е, що здійснюються за час, на протязі якого

амплітуда зменшується в е разів (8.7)

Коливний контур часто характеризують добротністю Q, яка визначається як величина, обернено пропорційна логарифмічному

декременту згасання

(8.8)

Із (8.8) випливає, що добротність контура тим вища, чим більше число коливань встигне здійснитися перш , ніж амплітуда зменшиться у е разів. Взявши замість його значення одержимо

(8.9)

Якщо згасання невелике ( ), то можна припустити, що

Тоді

(8.10)

Таким чином, формулу (8.10) можна використовувати у випадку незначного згасання.Можна також показати, що

(8.11)

де W – енергія, нагромаджена в контурі , а ΔW зменшення енергії в контурі за один період. Отже добротність контуру прямо пропорційна відношенню енергії, нагромадженої в контурі до витрати енергії в контурі за один період.

На закінчення відмітимо, що при β²>>ω₀² (тобто ) замість коливань відбувається аперіодичний розряд конденсатора. Опір контуру, при якому коливальний процес переходить в аперіодичний, називається критичним. Значення критичного опору R_кр визначається умовою звідки

R_кр =2 (8.13)

3.Для вивчення згасаючих коливань можна скористатися приведеною на рис.8.3

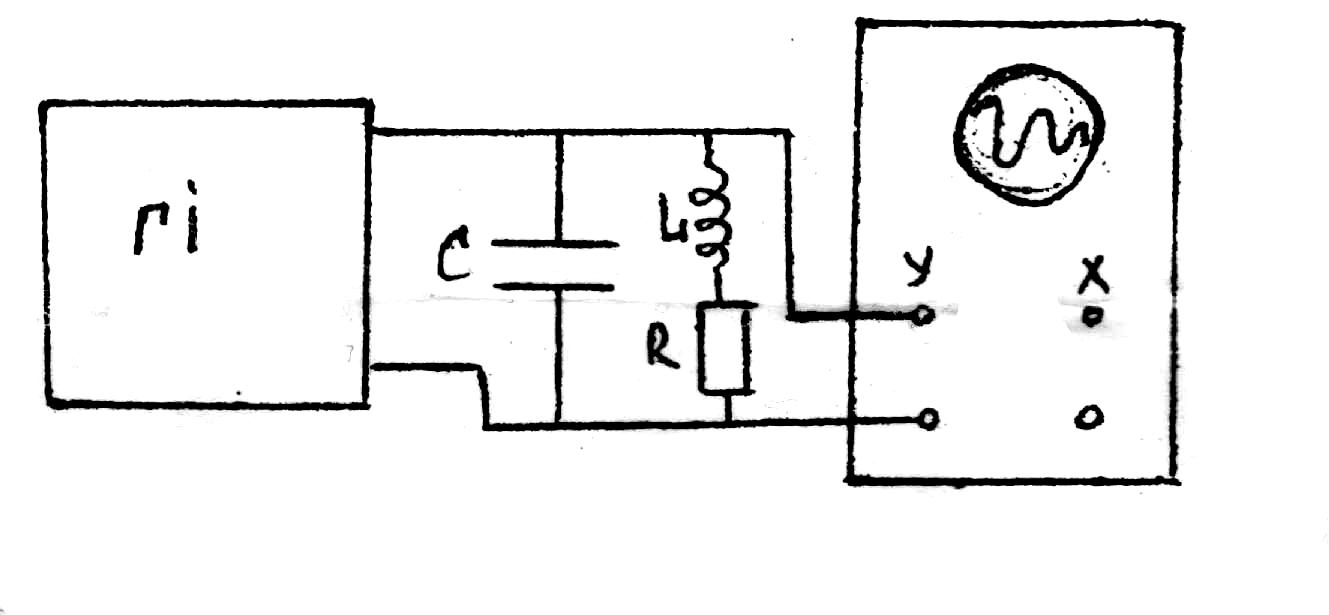
Рис.8.3. Блок – схема установки для дослідження згасаючих коливань.

Генератор імпульсів ГІ може видавати імпульси різної тривалості та різної частоти. Для більшої точності цих вимірювань слід максимально, в межах екрана осцилографа, збільшити зображення. Це проводиться поворотом ручки “верт.” Усиление” осцилографа.

V.З а в д а н н я т а х і д в и к о н а н н я р о б о т и.

Завдання 1. Визначення залежності періоду коливань в LC – контурі від його параметрів.

1. Зібрати схему, приведену на рис.8.3 при R=0 ^*. Включивши осцилограф та генератор імпульсів одержати стійку картину на екрані оцилографа при деякому значенні ємності. Визначити число коливань на екрані.

2. Змінити величину ємності 5 разів і повторити дії пункту 1. Дані експерименту занести в таблицю 1.

Т аблиця №1

Частота імпульсів генератора Гц	Ємкість Конденсатора Ф	Кількість коливань	Індуктивність котушки Гн	Період коливань С	Теоретичне Значення логарифмічного декременту
1
2
3

3. Порівняти теоретичне значення періоду коливань з експериментальними. Зробити висновок.

Завдання 2. Вивчення згасаючих коливань в L C – контурі .

1. Ввести в контур деякий опір R . Для вказаних керівником занять значень R зарисувати на кальку осцилограми при значених L та C завдання 1.

2. Виміряти з точністю до міліметра значення двох послідовних амплітуд. Дані експерименту занести в таблицю 8. 2.

Таблиця 8.2

№ п/п	Опір Контура Ом	Амплітуда мм	Амплітуда мм	Логарифмічний декремент	Період Тексп С	Теоретичні значення декременту
1
2
3

3. Для однієї пари значень L та C, послідовно збільшуючи включений опір магазина опору одержати криву аперіодичного розряду. Замітити величину цього опору і порівняти його із критичним значеням R_кр .Зробити основні висновки із одержаних результатів.

VI. Література.

[1] -стор. 247-251.

[2] -стор. 258-265

[3] -стор. 308-313.

[4] -стор. 416-418.

[8] -стор. 224-236.

[9] -стор.120-121

ViІ.Запитаня для контролю і самоконтролю.

1.Назвіть елементи ідеального коливного контуру.

2.Запишіть формулу енергії електричного поля кондесатора та енергії магнітного поля котушки із струмом ?

3.Який механізм перетворень енергії електричного і магнітного полів в контурі?

4. Запишіть диференціальне рівняння коливань в контурі та його розв’язок ,а також формулу Томсона.

5. Запишіть диференціальне рівняння коливань в реальному контурі та його розв’язок.

6: Зростає чи спадає період коливань в реальному контурі в порівнянні з ідеальним ? Чому ?

7:Дати визначення логарифмічного декременту згасання, добротності контура, критичного опору.

Лабораторна робота № 9 Зняття кривої намагнічування та петлі гістерезису за допомогою осцилографа

І. МЕТА РОБОТИ: вивчити фізичні основи явища намагнічування речовини у магнітному полі; ознайомлення з одним із способів зняття кривої намагнічування та петлі гістерезису.

ІІ. Для роботи потрібні: осцилограф, трансформатор, автотрансформатор, резистори на 100 Ом і 15 кОм, конденсатор, з’єднувальні провідники.

ІІІ. ТЕОРЕТИЧНІ ПИТАННЯ, ЗНАННЯ ЯКИХ НЕОБХІДНО ДЛЯ ВИКОНАННЯ РОБОТИ

1. Магнітні моменти електрона та атома.

2. Основні характеристики магнітного поля у речовині ( вектор магнітної індукції, вектор намагнічування, вектор напруженості), та зв’язок між ними

3. Магнітна проникність феромагнетика. Крива намагнічування. Петля гістерезису.

IV. Теореттичні відомості та опис установки.

1. Будь яка речовина яка вміщена у магнітне поле з індукцією , має здатність намагнічуватися. За цією ознакою всі відомі речовини називаються магнетиками. Механізм намагнічування речовини обумовлений наявністю магнітних моментів електронів і атомів, та впливу на них зовнішнього магнітного поля.

Намагнічена речовина утворює власне магнітне поле з індукцією яка додається до індукції зовнішнього магнітного поля , внаслідок чого у магнетику виникає результуюче магнітне поле з індукцією , тобто:

. 9.1

2. Явище намагнічування магнетика кількісно описують вектором намагнічення який є сумарним магнітним моментом всіх атомів чи молекул у елементі об’єму магнетика, тобто

, 9.2

де - деякий малий об’єм магнетика; магнітний момент окремого атома чи молекули.

Аналіз елементарних процесів у магнетиках вміщених у зовнішнє магнітне поле приводить до виразу

, 9.3

де - вектор напруженості магнітного поля, - магнітна стала.

3. Ветор має чудову властивість, яка формулюється теоремою про циркуляцію: циркуляція вектора напруженості магнітного поля по замкненому контурі l рівна алгебраїчній сумі охоплених контуром струмів

, 9.4

Намагніченість прийнято пов’язувати не із магнітною індукцією, а із напруженістю магнітного поля

, 9.5

де - магнітна сприятливість даного речовини

Із виразів 9.3 та 9.5 отримуємо

, 9.6

де - відносна магнітна проникність магнетика .

4. Досліди показують , що однорідні магнетики за характером намагнічення у зовнішньому магнітному полі можуть бути розділені на три групи. До першої належать речовини , які при розміщенні їх у магнітному полі намагнічуються так, що вектор намагнічення є паралельним векторові напруженості магнітного поля і однаково з ним напрямленим. Для цих тіл магнітна сприятливість , а магнітна проникність . Такі тіла називають парамагнетиками. До них належать більшість речовин, у тому числі хром, алюміній, марганець, вольфрам, розчини залізних і нікелієвих солей, кисень, азот і ряд інших. Магнітна сприйнятливість для парамагнетиків дуже мала – близько 10^-7 – 10^-4 одиниць.

До другої групи належать такі тіла, для яких вектор намагнічення є антипаралельним вектору , але протилежно направлений . Для цієї групи тіл, які називається діамагнетиками , а магнітна проникність . За абсолютним значенням величина така сама як і для парамагнетиків, а в ряді випадків і значно менша. Діамагнетиками є вісмут, мідь, ртуть, сурма, золото, цинк, сірка, кухонна сіль, вода, органічні сполуки... Для парамагнетиків і діамагнетиків , а, відповідно, і μ не залежать від Η :

До третьої групи, порівняно невеликої, але практично дуже важливої належать тіла, які при поміщенні їх у магнітне поле самі дуже сильно намагнічуються. Такі тіла називаються феромагнетиками. Це залізо, кобальт, нікель, сплави цих металів. Існують також феромагнітні сплави неферомагнітних речовин. Наприклад, сплав 61,5% міді, 23,5% марганцю і 15% алюмінію. В той час, як мідь є діамагнетик, а марганець і алюміній парамагнетики.

У залежності від призначення феромагнетиків до них ставлять різні вимоги. Виготовляючи спеціальні магнітні сплави і варіюючи їх обробку, можна одержати різні феромагнітні матеріали, що відрізняються своїми магнітними властивостями. Дуже важливим досягненням у галузі нових магнітних матеріалів є ферити і феромагнітні хімічні сполуки, які мають великий електричний опір (10-10⁴ Ом м).

5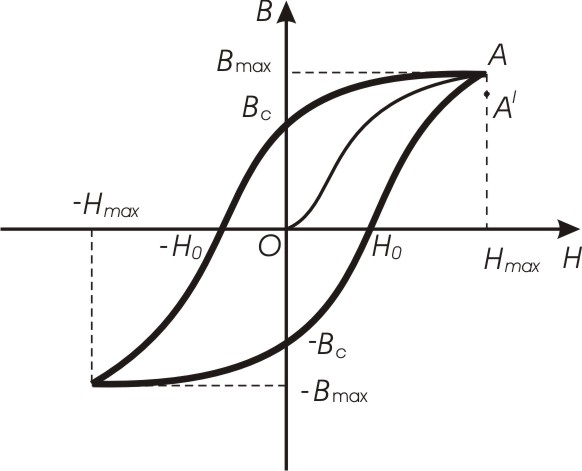 . Для феромагнетиків спостерігається нелінійна залежність χ та μ від напруженості магнітного поля Η, що приводить до цікавого фізичного явища. Якщо феромагнетик помістити у магнітне поле, то буде спостерігатися така закономірність. При збільшені напруженості зовнішнього магнітного поля від нуля до деякого максимального значення H_max індукція В також буде

з

Рис.9.2

ростати і досягне свого максимального значення В_max (див. рис.9.2, крива ОА). Криву ОА називають кривою намагнічування. Якщо тепер знижувати напруженість поля від Н_max до 0,. то індукція В також зменшується, однак лише до деякого значення В_С, відмінного від нуля. Отже, при відсутності магнітного поля феромагнетик виявиться все таки намагніченим. Крива АВ_с, що відповідає зміні Н від Н_max до 0, розміщена вище кривої ОА. Це явище пояснюється наявністю магнітного гістерезису, який полягає у тому, що зміна магнітної індукції відстає від зміни напруженості намагнічуючого поля. Величина індукції ОВ_С - називається залишковою індукцією. Щоб усунути залишкове намагнічення, треба зразок піддати дії протилежно напрямленого магнітного поля. Індукція при цьому зменшуватиметься і нарешті при деякому значенні Н=-Н₀ стане рівною нулю. Величина H₀ називається коерцитивною силою. Подальше збільшення поля Н викличе зміну напрямку індукції В (феромагнетик перенамагнітиться), яка досягне насичення при значенні поля –Н_{max .} Змінюючи напруженість поля від –Н_max до 0, одержимо криву А(-В_С) подібну до АВ_с. Відрізок 0-(-В) теж являє собою залишкову індукцію (умовно від'ємну), для усунення якої потрібно збільшити напруженість поля до деякого умовно додатного значення +Н_0. Збільшуючи напруженість поля від +H₀ до H_mах, одержимо точку А' відмінну від А. Максимальному значенню намагнічуючого поля тепер уже відповідатиме не +В_max, а дещо менше його значення.

Це пояснюється тим, що точку А ми одержали виходячи із магнітного нейтрального стану зразка, а точку А' одержали для зразка з початковою індукцією В. Якщо тепер продовжуватимемо процес намагнічування змінюючи напруженість магнітного поля в тих самих межах, одержимо подібну криву намагнічування, тільки точка А' дещо опуститься також. Але вже при третьому намагнічуванні гістерезисний цикл буде менш розімкнутим. Нарешті після багаторазового перемагнічування отримаємо замкнену криву, яка називається петлею гістерезисного циклу. Мінімальне число число таких перемагнічувань залежить від роду матеріалу.

Встановлюючи різні значення максимальної напруженості намагнічувчого поля Н_m1, Н_m2 і т.д. (рис.9.З) можна для даного матеріалу одержати сім'ю петель гістерезису, причому кожна з них з меншим значенням Н_m лежить всередині петлі з більшим значенням Н_m.

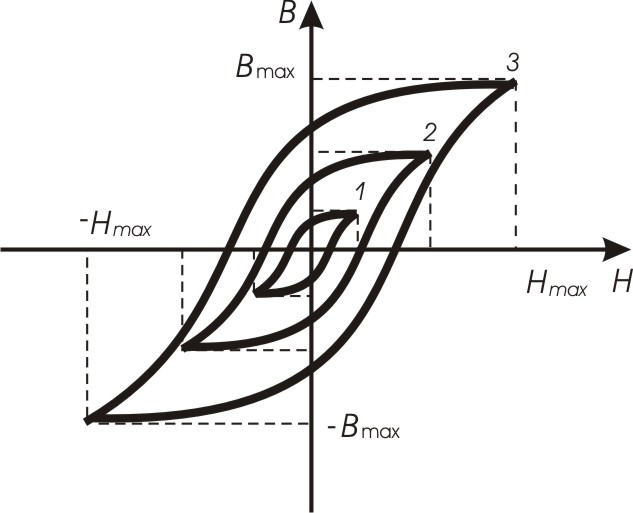
Рис 9.3.

При зростанні значення максимальної напруженості поля Н_m площа петлі гістерезису збільшується і при деякому його значенні Н_mах, що відповідає насиченню зразка, досягає максимуму. Ця найбільша петля називається граничною петлею гістерезису і є характеристикою даного феромагнітного матеріалу. Гранична петля гістерезису характеризується вершиною залишкової індукції В та коерцитивною силою Н_c. Вершини гістерезисних петель, яким відповідають різні значення максимальної напруженості намагнічуваного поля Н_m1, Н_m2 і т.д., розміщуються на основній кривій намагнічування, тобто на кривій магнітной індукції. Отже, крива залежності індукції В від Н являє собою геометричне місце вершин окремих петель гістерезисних циклів.

Експериментальне дослідження кривої намагнічування може бути проведене різними методами. Петля гістерезису отримується на екрані осцилографа, якщо на горизонтально відхиляючі пластини подати напругу -U_Х пропорційну Н, а на вертикально відхиляючі– подати напругу -U_y пропорційну В.

Принципова схема досліду приведена на рис.9.4.

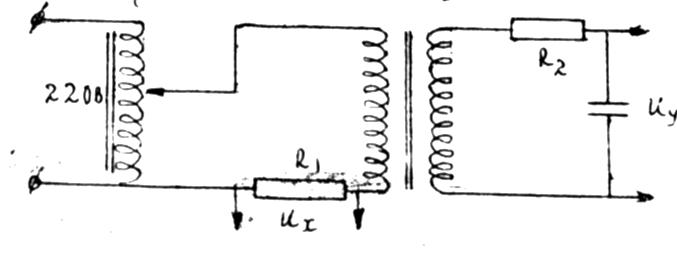
Рис.9.4

Досліджуваною речовиною є залізо, з якого виготовлено осердя трансформатора. Первинна обмотка трансформатора живиться через резистор R₁ змінним струмом I₁. Індукція магвітного поля в середині трансформатора рівна:

,

де n₁ – число витків в одиниці довжини обмотки. Тоді напруга на горизонтально відхиляючих пластинах буде задаватися таким виразом

, 9.7

Враховуючи залежність , дійдемо висновку, що .

У вторинній обмотці трансформатора виникне ЕРС індукції рівна

,

Де Ф - потік вектора магнітної індукції через поверхню, яку перетинають всі витки вторинної обмотки . Якщо S– площа, яку охоплює один виток , а n₂ - число витків тоді,

(8) і 9.9

Запишемо закон Ома для вторинного, кола нехтуючи його самоіндукцією

, 9.10

Якщо R₂ велике (R ≈ 10⁵ Ом), то то першим членом справа в формулі 9.3 можна знехтувати.

Звідки

Підставивши це значення у вираз:

, 9.1

де U_C напруга на конденсаторі; q – заряд конденсатора, отримаємо, що напруга яка подається на вертикальні відхиляючі пластинки осцилографа, рівна

9.12

Таким чином, на горизонтальні пластини подається напруга пропорційна Н, а на вертикальні - пропорційна В; в результаті на екрані отримуємо петлю гістерезису В= f(Н).

За кожний період синусоїдальної зміни струму електронний промінь на екрані буде описувати петлю гістерезису. В наслідок чого на екрані буде видно нерухому петлю гістерезису. Збільшуючи потенціометром напругу U_х будемо збільшувати амплітуду коливань і отримувати на екрані послідовно ряд різних за своїми площами петель гістерезису. Верхня точка петлі гістерезису знаходиться на кривій намагнічування.

Отже, для побудови кривої намагнічування необхідно зняти з екрана осцилографа координати n_x i n_y вершин петель гістерезисну та обчислити значення В₀ та В з формул (9.7) і (9.12), які для зручності переписані у виді:

, . (13)

Величини U_Х і U_У можна визначити, знаючи чутливість, тобто величину напруг u_x і u_y , які викликають відхилення електронного променя на одну поділку вздовж осей Х та Y при даному підсиленні. Тоді

, (9.13) (9.14)

де n_x і n_y - координати вершка петель гістерезису.

Підставляючи останні вирази для значення В і Н отримаємо:

(9.15)

(9.16)

де

(9.17)

(9.18)