Задача №3

С целью изучения средней месячной заработной платы и стажа работы работников торговых предприятий города, было проведено пятипроцентное выборочное обследование методом собственно-случайного бесповторного отбора.

Средняя месячная заработная плата 600 обследованных работников составила 15400 руб., среднее квадратическое отклонение – 2460 руб.

В выборочной совокупности 420 работников имеют стаж более 3 лет.

Определите для города в целом:

1. С вероятностью 0,954 возможные пределы средней месячной заработной платы.

2. С вероятностью 0,997 возможные пределы доли работников со стажем до 3 лет.

По полученным результатам сделайте выводы.

Решение:

 руб.   руб.; N = 600.

Вычислим:

1) С вероятностью 0,954 возможные пределы средней месячной заработной платы.

Учитывая, что  ;   найдем предельную ошибку выборки для средней по формуле:

,

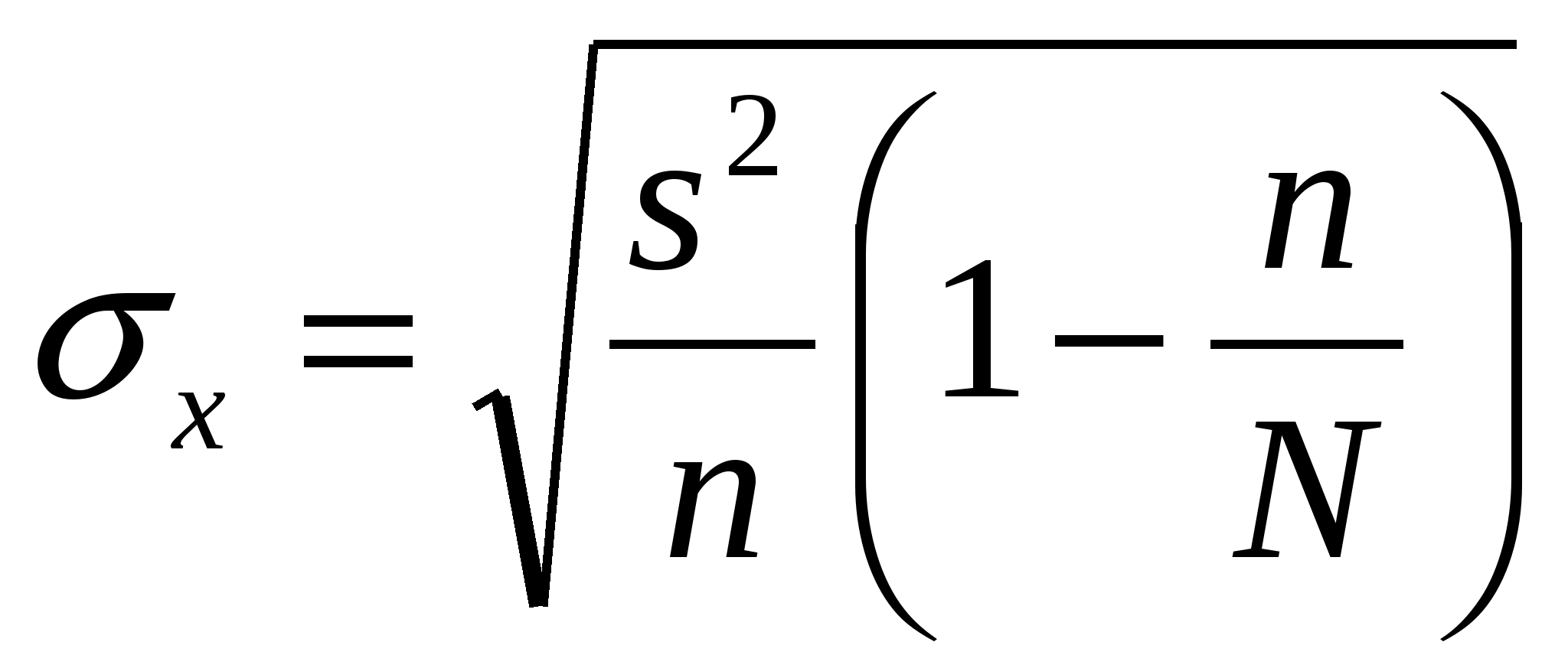- средняя квадратическая ошибка выборки.

;

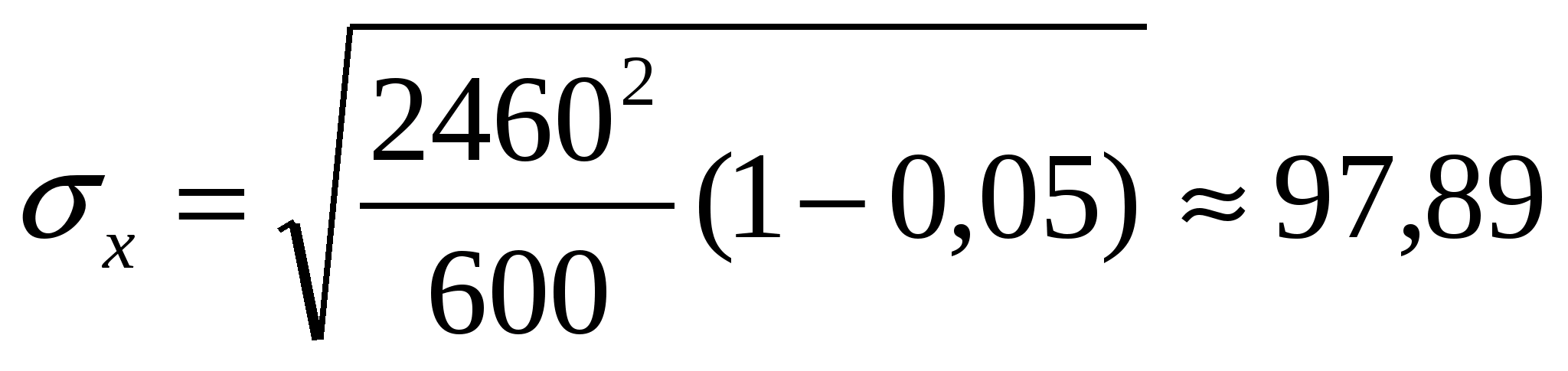По формуле   найдем возможные пределы средней месячной зарплаты:

;

 - возможные пределы средней месячной зарплаты.

2) С вероятностью 0,997 возможные пределы доли работников со стажем до 3 лет.

, где

 - объем выборки;

 – численность единиц выборочной совокупности, обладающих исследуемым признаком.

Учитывая, что найдем предельную ошибку выборки для доли по формуле:

,

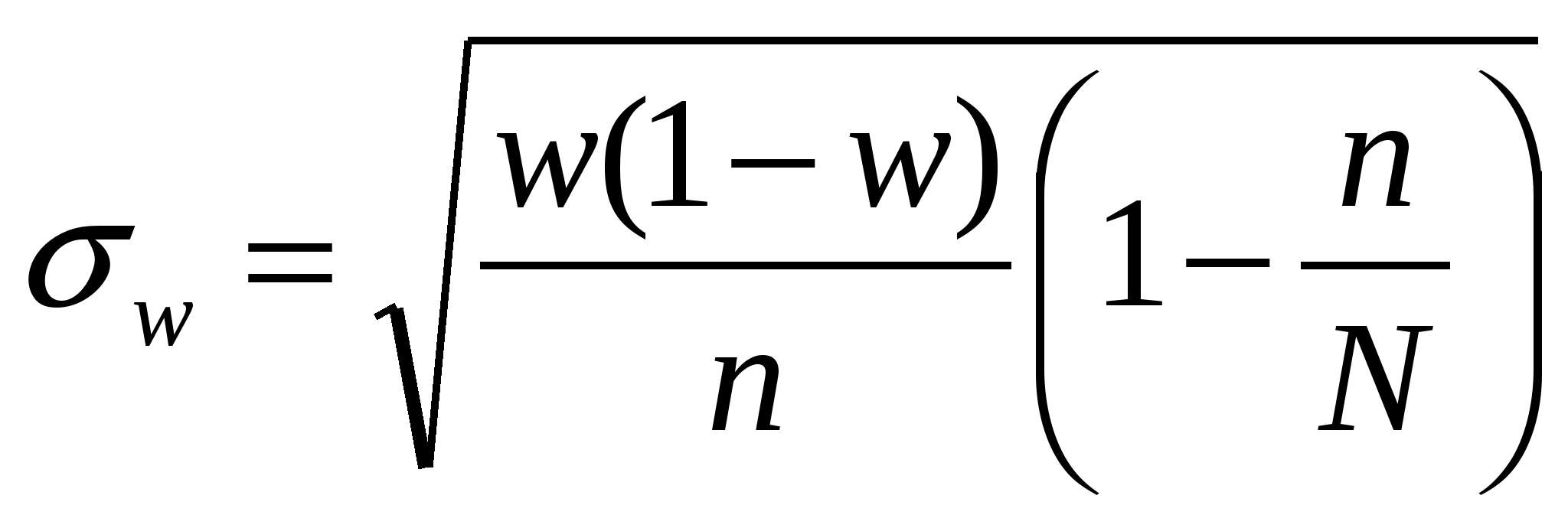- средняя квадратическая ошибка выборки.

;

.

По формуле   найдем возможные пределы доли работников со стажем до 3 лет:

;   или от 24,6 % до 35,4 %.

Задача №4

Имеется следующая информация о производстве товара «А» предприятием за 2000 – 2004 гг.:

Годы	2000	2001	2002	2003	2004
Объем выпуска, (тыс. шт.)	132	140	150	156	164

1. Для анализа погодовой динамики производства товара «А» определите следующие показатели динамики:

1. абсолютные приросты (цепные и базисные);

2. темпы роста и прироста (цепные и базисные);

3. средний абсолютный прирост и средний темп прироста.

Постройте график, характеризующий интенсивность динамики и сделайте выводы.

2. Произведите анализ общей тенденции производства товара «А» методом аналитического выравнивания.

1. фактические и теоретические уровни ряда динамики нанесите на график;

2. методом экстраполяции тренда вычислите прогнозное значение производства товара «А» в 2007 г.

Полученные результаты оформите в виде статистической таблицы. Сделайте выводы.

Решение:

1. Для анализа погодовой динамики производства товара «А» определим следующие показатели динамики:

- абсолютные приросты (цепные и базисные);

- темпы роста и прироста (цепные и базисные);

- средний абсолютный прирост и средний темп прироста.

Расчет показателей динамики от года к году (цепные)

Таблица 4.

Наименование показателя	Формула	2000	2001	2002	2003	2004
Абсолютный прирост, тыс. шт.		-	8	10	6	8
Коэффициент роста		-	1,061	1,071	1,040	1,051
Темп роста, %		-	106,06	107,14	104,00	105,13
Темп прироста, %		-	6,06	7,14	4,00	5,13