
- •1. Основы теории множеств
- •1.1. Введение в теорию множеств
- •1.1.1. Множества и подмножества
- •1.2. Алгебра множеств
- •1.3. Соотвествия между множествами и их элементами
- •2. Основы теории графов
- •2.1. Введение в теорию графов
- •2.1.1. Матричное представление графов
- •2.2. Разновидности графов и выполнение операций с графами
- •2.2.1 Действия над графами
- •3. Элементы математической логики
- •3.1. Логические функции и способы их представления
- •3.1.1. Основные логические операции
- •3.1.2. Законы и тождества алгебры логики
- •3.2. Элементарные логические функции
- •3.3. Нормальные и совершенные нормальные формы логических функций
- •3.3.1. Минимизация логических функций
- •4. Элементы теории матриц
- •4.1. Введение в теорию матриц
- •4.1.1. Произведение матриц
- •4.1.2. Матричная запись системы линейных алгебраических уравнений
- •4.2. Треугольные матрицы и характеристическое уравнение
- •4.2.1. Характеристическое уравнение. Собственные числа и собственные векторы
- •4.2.2. Связь между собственными числами и элементами матрицы. След матрицы
- •4.2.3. Собственные векторы
- •4.3. Теорема Кели-Гамильтона и ее применение
- •4.3.1. Преобразование подобия
- •4.4. Диагонализация матриц и функции от матриц
- •4.4.1. Функции от матриц
- •4.4.2. Матричные степенные ряды
- •4.4.3. Теорема Сильвестра
- •4.4.4. Норма матрицы
- •5. Основы теории систем
- •5.1. Динамическая система
- •5.2 Управление системой
- •5.3. Линейная динамическая система
- •5.3.1. Переходная матрица и матрица импульсных переходных функций линейной системы
2.1.1. Матричное представление графов
Любой граф, заданный множествами Х и Г или в виде рисунка, может быть также представлен с помощью матриц смежности и инцидентности.
В квадратной
матрице
смежности
![]() строки и столбцы соответствуют вершинам
графа. Для орграфа на пересечении i-той
строки и j-того
столбца матрицы значения элементов
образуются по правилу
строки и столбцы соответствуют вершинам
графа. Для орграфа на пересечении i-той
строки и j-того
столбца матрицы значения элементов
образуются по правилу
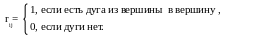
Д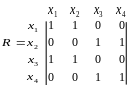 ля
графа на рисунке 2.2 матрица смежности
имеет вид:
ля
графа на рисунке 2.2 матрица смежности
имеет вид:
Единицы в главной диагонали матрицы свидетельствуют о наличии петель в графе.
Для неорграфа в матрице смежности на пересечении строк и столбцов стоят единицы, если вершины соединены ребрами. Матрица, построенная по этому правилу для графа на рисунке 2.3 имеет вид
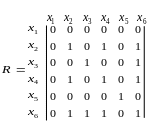
или соответствует
ранее построенной матрице отношений в
примере 1.16. Поскольку отношения в
неорграфе обладают свойством симметрии
![]() .
Следовательно, все ребра определяются
верхним правым треугольником матрицы,
включающим диагональ. Поэтому для
задания неорграфа можно использовать
треугольную матрицу.
.
Следовательно, все ребра определяются
верхним правым треугольником матрицы,
включающим диагональ. Поэтому для
задания неорграфа можно использовать
треугольную матрицу.
Существуют
разновидности матриц смежности. В
матрице
весовых соотношений элемент
![]() вместо 1 принимает значения веса связи
вместо 1 принимает значения веса связи
![]() ,
в матрице длин
– длины
ребра или дуги
.
,
в матрице длин
– длины
ребра или дуги
.
В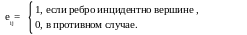 прямоугольной матрице
инцидентности
прямоугольной матрице
инцидентности
![]() строки соответствуют вершинам графа,
а столбцы – ребрам (дугам). Для неорграфа
на пересечении i-той
строки и j-того
столбца элементы матрицы образуются
по следующему правилу
строки соответствуют вершинам графа,
а столбцы – ребрам (дугам). Для неорграфа
на пересечении i-той
строки и j-того
столбца элементы матрицы образуются
по следующему правилу
Д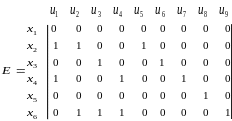 ля
графа, изображенного на рисунке 2.1в,
матрица инцидентности имеет вид
ля
графа, изображенного на рисунке 2.1в,
матрица инцидентности имеет вид
В каждом столбце матрицы Е не более двух единиц, поскольку каждое ребро соединяет две вершины. Столбцы, соответствующие петлям, содержат по одной единице.
Для орграфа в матрицу инцидентности заносится
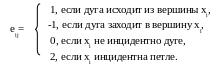
Д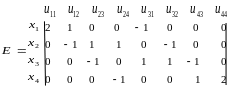 ля
графа на рисунке 2.2 матрица инцидентности
записывается в виде:
ля
графа на рисунке 2.2 матрица инцидентности
записывается в виде:
Матрица инцидентности, как и матрица смежности, однозначно определяет граф. Существуют приемы перехода от одной матрицы к другой.
С помощью матриц смежности можно установить изоморфизм графов. Для этого необходимо в матрице смежности одного графа проделать перестановки строк и столбцов. Если после очередной перестановки получим матрицу, тождественно совпадающую с матрицей другого графа, то графы изоморфны.
Помимо рассмотренных матриц, для описания графов используются матрицы контуров, расстояний и другие.
Контрольные вопросы
1) Из каких элементов состоит граф?
2) Какие различия имеются между ориентированным и неориентированным графами?
3) Как формируются матрицы смежности ориентированных и неориентированных графов?
4) Как формируются матрицы инцидентности ориентированных и неориентированных графов?
2.2. Разновидности графов и выполнение операций с графами
Граф, у которого хотя бы одна пара вершин соединена несколькими ребрами (дугами в одном направлении), называют мультиграфом. Ребра (дуги), связывающие одну и ту же пару вершин называют кратными.
Граф, не имеющий ребер и состоящий из изолированных вершин называется нуль-графом.
Число
ребер, инцидентных одной вершине
неорграфа, называют локальной степенью
вершины -
![]() .
Неорграф, у котрого
.
Неорграф, у котрого
![]() ,
,
то есть
все вершины имеют одинаковую степень
m,
называется однородным
степени m.
В орграфе
число исходящих дуг определяет полустепень
исхода
![]() ,
а число заходящих дуг – полустепень
захода вершины
,
а число заходящих дуг – полустепень
захода вершины
![]() .
Если
.
Если
![]() ,
,
то орграф также считается однородным степени m. Петля при определении степени вершины считается дважды: как исходящая дуга и как заходящая. Граф на рисунке 2.2 является примером однородного графа степени два.
Граф, все вершины которого попарно смежны, то есть между любой парой вершин имеется ребро, называется полным. Полный граф с m вершинами является одновременно и однородным степени m-1, поскольку каждая вершина соединена с m-1 остальными.
Если любые две вершины связаны цепью, граф называют связным. При определении связности орграфа можно не принмать во внимание направленность дуг. Если же для любой пары вершин найдется соединящий их путь (с учетом направленности дуг), то орграф считается связным. Графы, не отвечающие условию связности, состоят из связных подграфов, которые называются компонентами связности. На рисунке 2.4 приведен граф, состоящий из трех компонент связности.

Разновидностями связных графов являются эйлеровы и гамильтоновы графы. В первом имеется элементарный цикл, который включает все ребра, проходя через каждое ребро только один раз, и называется эйлеровым циклом. Во втором имеется гамильтонов цикл, проходящий через каждую вершину графа один раз.
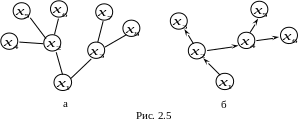
К связным
графам относятся также деревья. Деревом
называют
конечный связный неорграф, не содержащий
циклов (рисунок 2.5а). Вершина
![]() является корнем дерева, а другие вершины
с локальной степенью 1 называются
концевыми
является корнем дерева, а другие вершины
с локальной степенью 1 называются
концевыми
![]() .
Связный орграф без петель с корнем
и остальными вершинами, в каждую из
которых заходит только одна дуга,
называется прадеревом
(рисунок
2.5б).
.
Связный орграф без петель с корнем
и остальными вершинами, в каждую из
которых заходит только одна дуга,
называется прадеревом
(рисунок
2.5б).
Несвязный граф без циклов называется лесом. Компонентами связности леса могут быть деревья, а также отдельные ребра и изолированные вершины, являющиеся частным случаем деревьев. На рисунке 2.6 показан пример такого графа.

Если пометить вершины одного из деревьев нулями и единицами, как показано на рисунке 2.6, то записав пути от корня до концевых вершин, получим комбинации 000, 001, 010, 011.
Дерево, являющееся частичным графом графа , называется деревом покрывающим граф G. На рисунке 2.3б жирными линиями выделено такое дерево. Наименьшее число ребер, которые надо удалить из графа, чтобы он стал ациклическим (то есть не содержащим циклов), определяется цикломатическим число графа. Если граф имеет n вершин, m ребер и k компонент связности, то его цикломатическое число равно
![]() .
.
Для графа на рисунке
2.3б для получения покрывающего дерева
необходимо удалить
![]() ребра.
ребра.
